[USACO25FEB] Bessie's Function G 题解

题目传送门

洛谷P11842
USACO题目
USACO题解

前言

本文为作者在参考多篇题解后觉得个人难以读懂（主要原因为作者太菜细节缺失），本文将通过配图来解决无法读懂这一问题。

题意简述

给定 \(a_1,a_2,\cdots,a_n\) 以及修改每个 \(a_i\) 的代价 \(c_i\) ，希望通过对于每个 \(i\) ，都有 \(a_i=a_{a_i}\)

为了方便给出两组样例及配图（蓝字为有向边终点的修改权值）

样例1

输入

5
2 4 4 5 3
1 1 1 1 1

输出

3

图

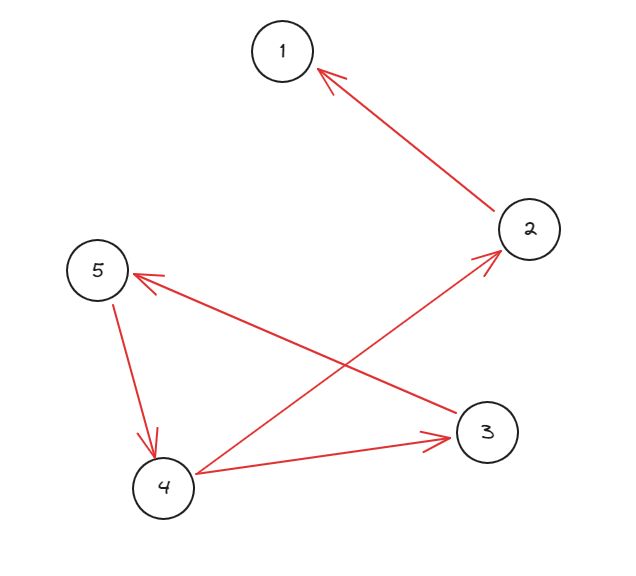
image

说明

将 \(a_1,a_4,a_5\) 分别改为 \(1,4,5\)后，我们得到
image

样例2

输入

8
1 2 5 5 3 3 4 4
9 9 2 5 9 9 9 9

输出

7

图

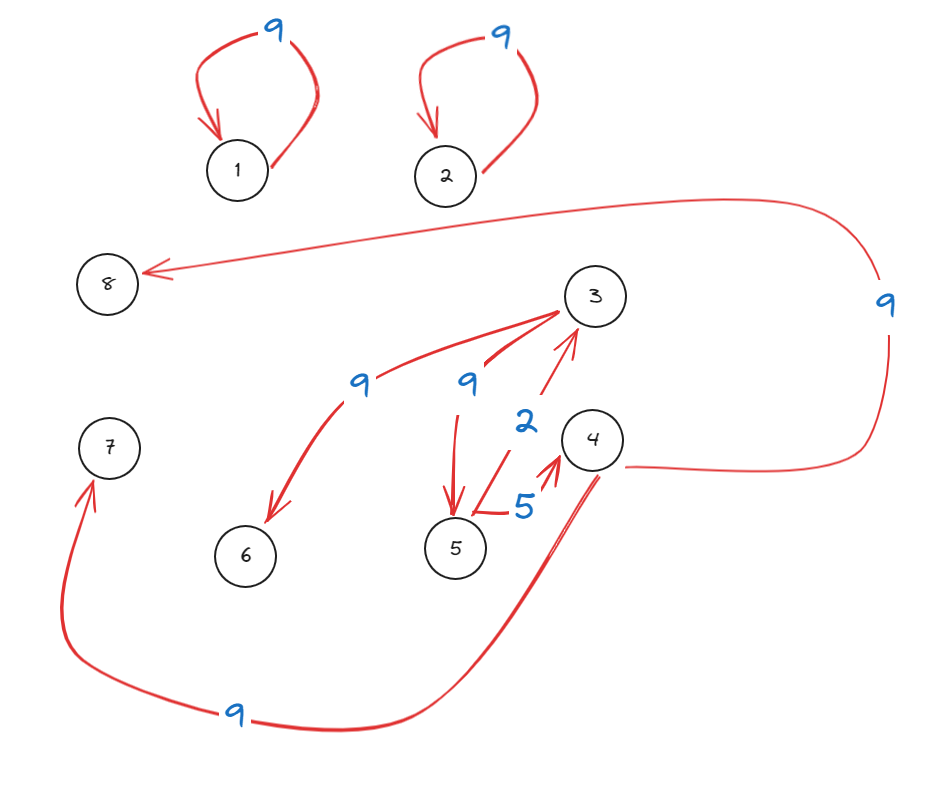
image

思路

基环树版子题。
我们想到对于每组 \(a_i\) ，都建立一条从 \(a_i\) 到 \(i\) 的单向边，并定义 \(a_i\) 为 \(i\) 的父亲。
这样一来，题目条件变为，从一个点 \(i\) 出发，其父亲等于其祖父，换句话说，从一个点 \(i\) 出发，逆箭头走一步等于再走一步。
进一步地， 要么 \(i\) 为自环，要么 \(a_i\)（\(i\) 的父亲） 为自环。
显然若 \(i\) 不满足条件，将 \(a_i\) 修改为 \(i\) 最划算。此处多题解都有证明，本处不再赘述。
由上图，显然这是一个外向基环树森林（每个点有且仅有一条入边），例如上图在每个联通块的环中删掉一条边后，根节点有 \(1,2,(3\ \text{or}\ 5)\)。不妨设整张图联通，否则可以按不同联通块考虑。

基环树典型操作：从环上选一边特判，然后树形dp剩下的两颗树。（很玄学看不懂就别看了）

本题中，我们按照USACO的思路讨论两种情况（Subtask3和Subtask4）
Subtasks:

  • Input 3: \(N≤20\)
  • Inputs 4-9: \(a_i≥i\)
  • Inputs 10-15: All \(a_i\) are distinct.
  • Inputs 16-21: No additional constraints.

Subtask 3

Subtask3(Inputs4-9)中，每个 \(a_i\) 都大于等于 \(i\)，这保证了图上除了自环不存在其他环[1]，
例如（USACO样例太大，此处为作者自制）：

7
1 3 4 6 5 7 7
1 1 1 1 1 1 1

图：
image

手玩几组数据，我们注意到好吧图画出来还真挺显然的，整张图上所有连通块不是自环就是“一颗树”，但是树的根节点是个自环。
对于所有自环的（如上图就是 \(1,5,7\)，是的，基环树上的自环也算），直接把 \(c_i\) 修改为 \(0\)，这样方便后面累加修改值和树形dp初始化时不用讨论。

树形dp

设 \(dp_{i,0}\) 表示以 \(i\) 为根的子树修改最小值，其中 \(i\) 不作修改。
设 \(dp_{i,1}\) 表示以 \(i\) 为根的子树修改最小值，其中 \(i\) 作修改，修改 \(a_i=i\)。
设 \(u\) 的儿子集合为 \(\text{son}_u\)，
则我们有

  1. 若根不作修改，则根的儿子必须修改。因此
    \(dp_{i,0}=\sum_{j\in{\text{son}_i}}dp_{j,1}\)
  2. 若根作修改，则根的儿子可修可不修。因此
    \(dp_{i,1}=c_i+\sum_{j\in{\text{son}_i}}\min\{dp_{j,0},dp_{j,1}\}\)

从根开始递归计算即可，注意要特判掉回到根节点的那条边，防止重复计算。
最后的答案应为 \(dp_{i,1}\)，因为根节点应为一个自环，必须修改

代码[2]：

int dfs(int u, int root)
{
    dp[u][0] = 0;
    dp[u][1] = c[u];
    for (auto v: son[u]) {
        if (v == root) continue;
        dfs(v, root);
        dp[u][0] += dp[v][1];
        dp[u][1] += min(dp[v][0], dp[v][1]);
    }
    return dp[u][1];
}

Subtask 4

Subtask4(Input10-15)中，每个 \(a_i\) 都不同。
例如（此处同为作者自制）：

7
5 2 4 6 1 7 3
1 1 1 1 1 1 1

看图：
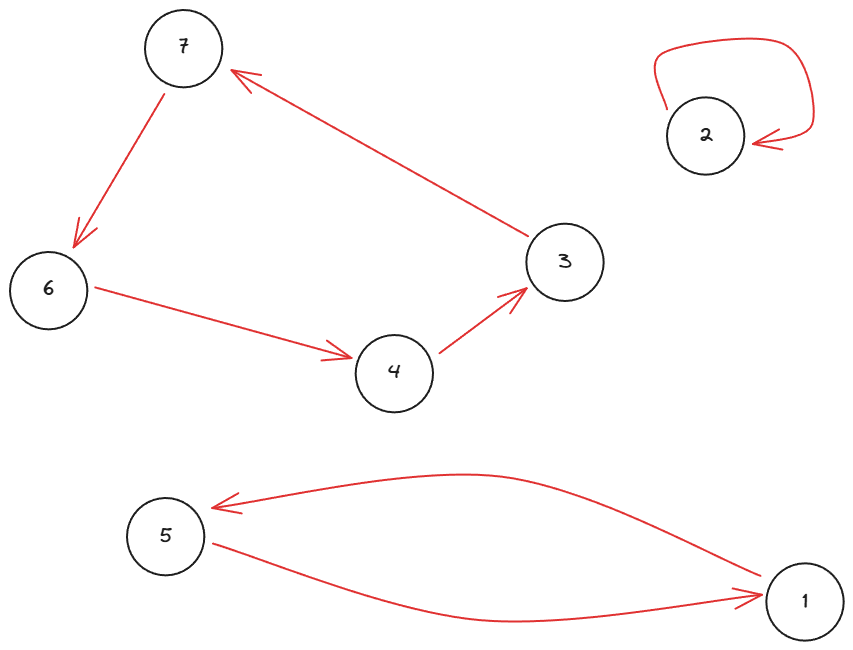
image
显然，整个图上的联通块都是环。至于证明，留给读者自证好了（逃）。
怎么解决环上问题呢？
首先特判自环。
剩下的环中，随便选一条边，然后就又双叒叕★注意到★这谁注意得到啊喂在此边的最终解决方案里，至少有一个点需为自环（FAQ：可是两个点都为自环会浪费吧 ANS：这个显然树形dp会在枚举一端点时考虑到要不要修改另一端点的，因此此处不需考虑）。
那么，我们分别求出将此边上两端点修改为自环后，以其为根节点做树形dp的代价，然后取最小值。
例如，对于上图来说，3到7这一条边，我们直接选择3作根节点树形dp（此处不需要修改是因为树形dp的深搜会自动考虑该情况的），得到结果等于对于（3->7->6->4）这一棵树的dfs结果，也就是2，对于7我们得到同样的结果，因此答案为2，累加到总答案上。

合并两个Subtask

我们再来看这张图：
image
其中含有的环可以用Subtask4的思路，随便选一条边，将其分开树形dp:
image
自认为此解比USACO官方的分类讨论简单点：

Full Solution:
We can combine the ideas from subtask 3 and 4
. For each component, locate the cycle using Floyd's Algorithm or DFS. If the cycle's length is 1, we can just use the solution from subtask 3
. Otherwise, use the idea from subtask 4 to convert the cycle into 2 instances of a rooted tree and solve each with subtask 3's solution.
大意：将环做法和树做法融合。每次先用Floyd算法或深搜找环，然后判环的长度。若为1，直接树形dp。否则，用Sub4的思想，断环为两树，再套sub3的做法。

VS 我的改进

对于每个联通块直接找环，然后不管环的长度直接断环为链，如果是自环无影响，因为一开始就初始化 c[自环点]=0 了

正确性证明：

如何保证这样一定涵盖了最优解呢？
接下来纯粹讨论一下断环为链的做法没有遗漏的原因。
首先证明若环上一边的两点中皆无自环，则一定不合法。
证：设此边起点为x，则x的父亲即此边终点，若两者皆不是自环则根据定义不合法。Q.E.D.
然后，就讨论两点的修改这步，我们是分开讨论，互不影响，没有任何问题。由于保证了这条边的合法性，所以得到
这条：此边在图中等于不存在，无需考虑。因此，原来的恶心基环树变成了一个热情的小哈可爱的树，终于可以正常树形dp辣

代码

#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 2e5 + 5;
int n, a[N];
vector<int> son[N]; // a[i]的反函数
int c[N]; // 修改a[i]的代价
int r1, r2; // a[r1] = r2
bool vst[N];
int dp[N][2]; // 子树根为u，a[u]!=u(0)或a[u]==u(1)的最小代价
void find_loop(int u, int rt)
{
	vst[u] = 1;
	for (auto v: son[u]) {
		if (v == rt) {
			r1 = v;
			r2 = u;
			return ;
		}
		if (vst[v]) continue;
		find_loop(v, rt);
	}
}
int dfs(int u, int rt)
{
	dp[u][0] = 0;
	dp[u][1] = c[u];
	for (auto v: son[u]) {
		if (v == rt) continue;
		dfs(v, rt);
		dp[u][0] += dp[v][1]; // a[u]!=u,所以a[v]必须等于v
		dp[u][1] += min(dp[v][0], dp[v][1]); // a[u]==u,所以a[v]可以等于v或不等于v
	}
	return dp[u][1];
}
signed main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cin >> n;
	for (int i = 1; i <= n; ++i) {
		cin >> a[i];
		son[a[i]].push_back(i);
	}
	// 需满足条件：对于任意i，a[a[i]]=a[i]
	// 显然将a[i]修改为i最划算
	for (int i = 1; i <= n; ++i) {
		cin >> c[i];
		// is indempotent
		if (a[i] == i) c[i] = 0;
	}
	int ans = 0;
	for (int i = 1; i <= n; ++i) {
		// for each component, locate the loop use dfs
		if (vst[i]) continue;
		r1 = r2 = 0;
		find_loop(i, i);
		if (r1 == 0) continue; // no loop
		// choose any arbitrary edge in the loop
		// break the edge and make the two vertices indempotent
		int res1 = dfs(r1, r1);
		int res2 = dfs(r2, r2);
		ans += min(res1, res2);
	}
	cout << ans << '\n';
	return 0;
}

后记

作者制作不易，如果您读懂或觉得有帮助，请留个赞再走qwq
否则，也请您指出不足之处，谢谢！

  1. 证明：假设环由 \(a_{x_1}\rightarrow x_1=a_{x_2}\rightarrow x_2=a_{x_3}\rightarrow\cdots x_{k-1}=a_{x_k}\rightarrow x_k=a_{x_1}\) 构成，则显然 \(a_{x_1}\geq x_1=a_{x_2}\geq\cdots x_{k-1}=a_{k}\geq x_k=a_{x_1}\Longrightarrow x_1\geq x_k\geq x_1\Longrightarrow x_1=x_k\)，即此环上起点等于终点，所以此环长度为1，为自环。 ↩︎

  2. 注意，本文除了最后贴上AC代码，其余代码都为作者写博时手敲，不保证正确性。 ↩︎

posted @ 2025-08-23 20:25  peter_code  阅读(41)  评论(0)    收藏  举报