最大公约数与最小公倍数的详细讲解及求法

最大公约数与最小公倍数的详细讲解及求法

一、最大公约数概念：

如能够被一个整数整除的整数称为其倍数；能够整除一个整数的整数成为其约数；如果一个数既是数A的约数，又是数B的约数，则最大的这个数称其为A，B的最大公约数。

二、辗转相除法求最大公倍数：

有两个整数x、y（x和y谁大都可以，不影响结果），x除以y得到的余数去除以除数（当前除数是x,值是y的值），再用出现的余数去除以除数（当前除数是上一次的余数），以此类推，直到最后余数为0为止。如果求两个数的最大公约数，最后的除数就是两个数的最大公约数。

#include <iostream>
int main()
{
	int x, y, v = 0;
	std::cin >> x;
	std::cin >> y;
	while (y) {
		v = x % y;
		x = y;
		y = v;
	}
	std::cout << x << std::endl;
	return 0;
}

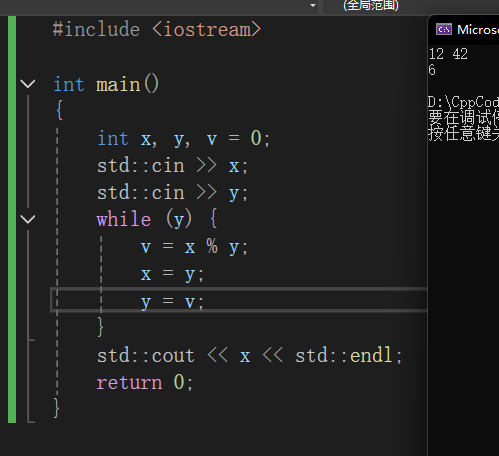
举例：计算 12 和 42 的最大公约数

我们输入 x = 12，y = 42。

循环开始


第 1 次循环

计算 v: v = x % y -> v = 12 % 42。12 除以 42 商为 0，余数为 12。所以 v = 12。

更新 x: x = y -> x = 42。

更新 y: y = v -> y = 12。

循环后状态:

x = 42

y = 12

v = 12


第 2 次循环

计算 v: v = x % y -> v = 42 % 12。42 除以 12 商为 3，余数为 6。所以 v = 6。

更新 x: x = y -> x = 12。

更新 y: y = v -> y = 6。

循环后状态:

x = 12

y = 6

v = 6


第 3 次循环

计算 v: v = x % y -> v = 12 % 6。12 除以 6 商为 2，余数为 0。所以 v = 0。

更新 x: x = y -> x = 6。

更新 y: y = v -> y = 0。

循环后状态:

x = 6

y = 0

v = 0


第 4 次循环

条件检查: while (y) -> while (0)。条件为假，循环终止。

执行输出: std::cout << x << std::endl;。此时 x 的值是 6。

程序输出: 6

三、求最小公倍数以及基本概念：

如果一个数既是x的倍数又是y的倍数，那么我们就把这个数看作是x和y的公倍数，若这个数在x,y的所有公倍数里为最小的，那这个数就是最小公倍数。

四、求最小公倍数（两种方法）：

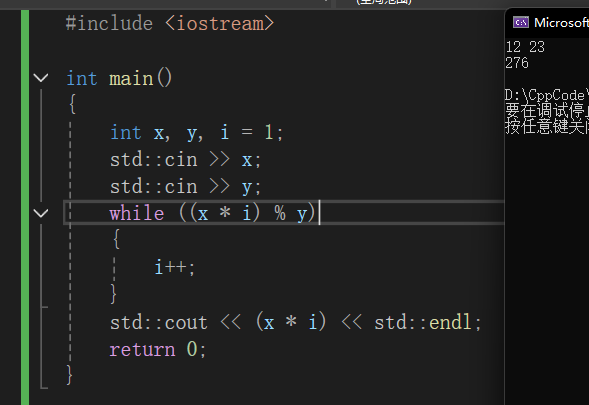
//直接求最小公倍数
#include <iostream>

int main()
{
    int x, y, i = 1;
    std::cin >> x;
    std::cin >> y;
    while ((x * i) % y)
    {
        i++;
    }
    std::cout << (x * i) << std::endl;
    return 0;
}

x = 12;

y = 23;

当 (12 * i) % 24 == 0 时，也就是(x * i) 既可以整除x,也可以整除y;当且仅当此时(x * i)为最小公倍数。

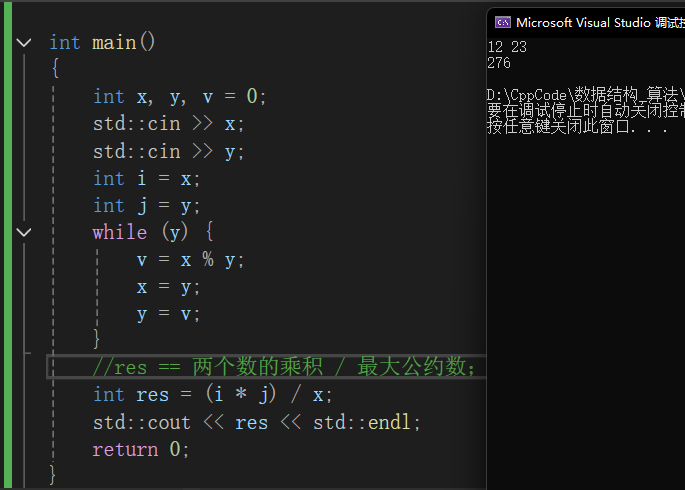
利用最大公约数求最小公倍数：

已知x，y的最大公约数为v，最小公倍数为j，则有公式为x * y = 最大公约数v * 最小公倍数j;

所以可以用该公式求出最小公倍数:

//利用最大公约数求最小公倍数
#include <iostream>

int main()
{
	int x, y, v = 0;
	std::cin >> x;
	std::cin >> y;
	int i = x;
	int j = y;
	while (y) {
		v = x % y;
		x = y;
		y = v;
	}
	//res == 两个数的乘积 / 最大公约数；
	int res = (i * j) / x;
	std::cout << res << std::endl;
	return 0;
}