回溯-组合
回溯-组合
回溯法的本质是穷举,其主要是为了解决n个for循环的问题,在for循环中套着递归从而不断实现for循环。回溯法解决的问题都可以抽象为树形结构,一般是在给定集合是取出符合一定规则的数据。集合的大小构成树的宽度,也即第一层的for循环遍历的范围,递归的深度构成树的深度,也就暴力for循环实现的层数。
可以理解为回溯实现不同层级的for循环,通过递归函数进入下一层,同时控制每层的遍历范围。一旦找到合适的子结果或者当前结果到达最底层,终止当前遍历并返回上一层继续for 循环遍历。回溯实际上是暴力搜索,减少其复杂度的方式主要靠剪枝优化。
回溯法的模板为:
void backtracking(参数){
if(终止条件){
存放结果;
return;//返回上一层for循环
}
for(选择:本层集合中的元素(树中节点孩子的数量))//也即当前层for循环的遍历范围{
处理节点;
backtracking(路径,选择列表);//实现递归
回溯,撤销处理结果
}
}
组合问题是回溯算法中常见的问题,大体包括在一个或者多个集合中选择元素,元素选择可否重复选择等问题,对字符串实现分割使其满足条件也是组合问题。
Part1 单集合和多集合
这个是在单个集合里寻找满足条件的组合,而且是不可重复选择的
该问题可抽象为如下树结构:
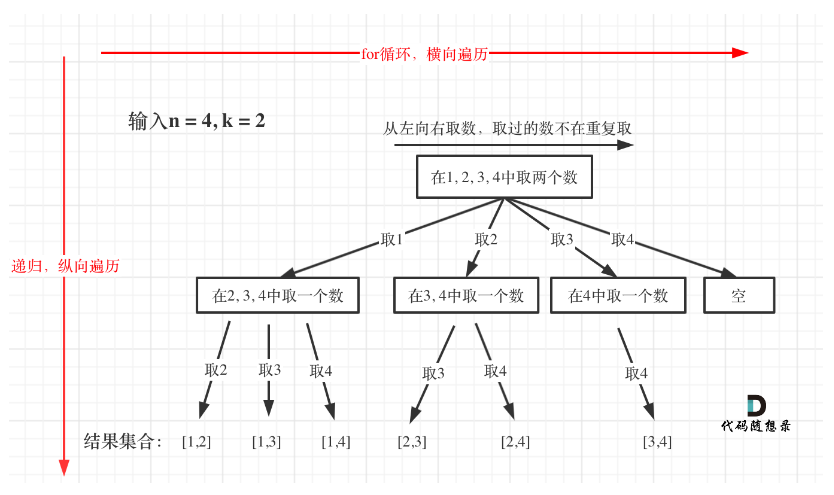
其代码如下:
Class Solution(){
private:
vector<vector<int>> result;//保存结果
vector<int> path;//单个路径的叶子节点
void backtracking(int n,int k,int index){
if(path.size()==k){
result.push_back(path);//保存符合条件的叶子节点
return;
}
for(int i = index;i<=n;i++){//设置index是为了控制每层for循环的起始位置
path.push_back(i);//保存当前的节点
backtracking(n,k,i+1);//进入下一层for循环,同时因为是不重复取元素,故下一层的for循环从第i+1开始
path.pop_back();//当前叶子节点已被保存,回退到上一层的for循环遍历,故需要撤销元素,使之返回到上一层,例如当n=4,k=2时,[1, 2]这个叶子节点被保存,此时删除2,是为了保存下一个叶子节点即[1,3]
}
}
public:
vector<vector<int>> combine(int n,int k){
backtracking(n,k,1);
return result;
}
};
上述代码存在剪枝优化的余地,考虑我们需要的是k个数的组合,因此在第i层for循环遍历的时候,此时路径path已经保存了i-1个元素,还需要k-i+1个元素,所以第i层for循环遍历的终止位置应该是n-(k-i+1)+1=n-(k-i),即n-(k-(path.size()+1))=n-(k-path.size())+1,因此for循环可以改为
for(int i = index;i <= n-(k-path.size()))+1;i++)
由于共有\(C^k_n\)种组合,每种组合需要\(O(k)\)的时间复杂度,因此时间复杂度为\(O(C^k_n\times K)\).空间复杂度取决于递归深度,即系统栈所用空间为\(O(n)\).
leetcode17
与上述单个集合中求组合的问题不同的是,这个问题是在多个集合中求组合。具体的不同是在for循环中遍历起始位置的不同。
class Solution{
private:
const string letterMap[10]={
" ",
" ",
"abc",
"def",
"ghi",
"jkl",
"mno",
"pqrs",
"tuv",
"wxyz",
};
public:
vector<string> result;
string s;
void backtracking(const string& digits,int index){
if(index == digits.size()){//index即按键字符串索引,用以进入不同的按键子集
result.push_back(s);
return;
}
int digit = digits[index]-'0';// 将当前按键数字变为int型
string letter = letterMap[digit];//取按键对应的字符串
for(int i = 0;i<letter.size();i++){//由于是不同集合的组合,故每层for循环只需要遍历完当前子集的整个范围即可。
s.push_back(letter[i]);
backtracking(digits,index+1);//进入下一个按键的子集
s.pop_back();
}
}
vector<string> letterCombinations(string digits){
if(digits.size()==0){
return result;
}else{
backtracking(digits,0);
return result;
}
}
};
该算法的时间复杂度是\(O(3^m\times 4^n)\),其中m为输入对应3个字母的数字个数,n为输入对应4个字母的数字个数,空间复杂度则是\(O(m+n)\),空间复杂度主要取决于哈希表以及递归调用层数。
总结:何时需要index控制for循环遍历的起始位置?
一个集合求组合,需要index;
多个集合求组合,集合之间互相不影响,不需要index.
Part2 重复与去重
给定无重复元素的数组candidates和目标数 target,找出candidates中所有可以使数字和为target的组合。candidates中的数字可以被无限制选取。解集不可包含重复的组合。
由于数字可被无限制选取,故树的深度是由target制约的。一旦元素总和超过target,则返回至上一层for循环。由于这个是单集合中选取组合,仍然需要index控制每层for循环的起始位置,至于集合中元素可以被无限制选取,则对于第i层循环,遍历到第i 个元素时,控制下一层的for循环起始位置为i,则可实现集合元素的无限制选取。
class Solution{
private:
vector<vector<int>> result;
vector<int> path;
void backtracking(int sum,int target,const vector<int>& candidates,int index){
if(sum>target){
return;
}
if(sum == target){
result.push_back(path);
return;
}
for(int i = index;i<candidates.size();i++){
sum += candidates[i];
path.push_back(candidates[i]);
backtracking(sum,target,candidates,i);//i表示可以重复读取当前的元素
sum -= candidates[i];
path.pop_back();
}
}
public:
vector<vector<int>> combinationSum(vector<int>& candidates, int target){
backtracking(0,target,candidates,0);
return result;
}
}
这种求和问题,我们可以利用排序来优化剪枝,排序后一旦当前求和sum大于target,该层for循环后面的遍历全部是满足大于sum的,因此就可以退出该层。因此对总集合排序后,如果本层的sum+candidates[i]大于 target,则可以结束本层的for循环。
即
for(int i = index;i<candidates.size()&&sum+candidates[i] <= target;i++)
//candidates需要先排序再进行回溯
给定数组candidates (存在重复数字)和一个目标数target,找出candidates中所有可以使数字和为target的组合,candidates中的每个数字在每个组合中只能使用一次。解集中不能包含重复的组合。
难点在于集合即数组candidates中存在重复元素,但是解集中不能有重复的组合。树形结构去重需要考虑两个维度,即同一个树枝和同一个树层,由于每个元素只能使用一次,利用i+1则可以实现每个元素的不重复使用。由于解集中不能包含重复的组合,需要同一树层上所取元素进行去重,例如[1,1,2],取第一个1之后选择[1,2], 取第二个1之后同样再选择[1,2],这样就会造成解集中包含相同的组合。对树层去重,还需要先对集合排序,如图:
class Solution{
private:
vector<vector<int>> result;
vector<int> path;
void backtracking(vector<int>& candidates, int target, int sum, int index){
if(sum == target){
result.puah_back(path);
return;
}
for(int i = index;i<candidates.size()&& sum+candidates[i] <= target;i++){//剪枝操作,对集合排序后在某层第i个值求和若出现sum>target,则该层第i个值之后的元素完全不用遍历。
if(i>index&&candidates[i]==candidates[i-1]){//树层上去重,防止解集合中出现重复的组合
continue;
}
sum += candidates[i];
path.push_back(candidates[i]);
backtracking(candidates,target,sum,i+1);//i+1是为了保证集合中的元素不重复取用
sum -= candidates[i];
path.pop_back();
}
}
public:
vector<vector<int>> combinationSum2(vector<int>& candidates, int target){
sort(candidates.begin(),candidates.end());
backtracking(candidtaes,target,0,0);
return result;
}
};
找出所有相加之和为n的k个数之和,组合中只允许含有1-9的正整数,并且每种组合中不存在重复数字。该题和组合总和一样,只是将集合的的范围即横向遍历范围限制在 1-9.
同样由于是单集合,需利用index控制for循环的起始位置
class Solution{
private:
vector<vector<int>> result;
vector<int> path;
void backtracking(int sum,int k,int n,int index){
//剪枝优化
//if(sum > n){
//return;
//}
if(path.size() == k){
if(sum == n){
result.push_back(path);
return;
}
}
for(int i = index;i<=9;i++){
sum += i;
path.push_back(i);
backtracking(sum,k,n,i+1);
sum -= i;
path.pop_back();
}
}
public:
vector<vector<int>> combinationSum3(int k, int n){
backtracking(0,k,n,1);
return result;
}
};
剪枝优化:由于集合可以视为已排序,第i层遍历时可根据path.size()的大小确定该层for循环遍历的终止位置,即将for循环更改为
for(int i = index;i<=9-(k-path.size())+1;i++)
当sum大于n,也没必要往后遍历,也可进行相应的剪枝操作。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号