强化学习理论-第8课-值函数近似

当state space太大的时候，需要用一个函数来对state value 或action value进行近似，方便处理

1. Algorithm for state value estimation

1.1 Objective function

这里\(d_{\pi}\)是权重，可以决定哪个state权重比较大，就让它的误差变得更小

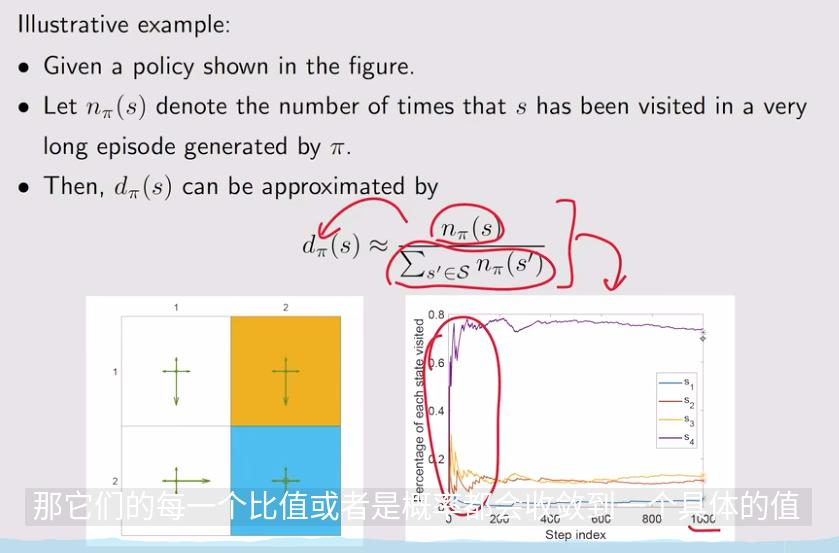
这里的\(P_{\pi}\)和贝尔曼公式里的是一个，里面每个元素代表当前状态到下一个状态的转移的概率

1.2 Optimization algorithms

1.3 Selection of function approximators

2. Sarsa with function approximation(action value)

3. Q-learning with function approximation

4. Deep Q-learning

5. Deep Q-learning-Experience replay

6. Deep Q-learning-implementation and example

def gfv(self, fourier: bool, state: int, ord: int) -> np.ndarray:
        """
        get_feature_vector
        :param fourier: 是否使用傅里叶特征函数
        :param state: 状态
        :param ord: 特征函数最高阶次数/傅里叶q(对应书)
        :return: 代入state后的计算结果
        """

        if state < 0 or state >= self.state_space_size:
            raise ValueError("Invalid state value")
        y, x = self.env.state2pos(state) + (1, 1)
        feature_vector = []
        if fourier:
            # 归一化到 -1 到 1
            x_normalized = x / self.env.size
            y_normalized = y / self.env.size
            for i in range(ord + 1):
                for j in range(ord + 1):
                    feature_vector.append(np.cos(np.pi * (i * x_normalized + j * y_normalized)))

        else:
            # 归一化到 0 到 1
            x_normalized = (x - (self.env.size - 1) * 0.5) / (self.env.size - 1)
            y_normalized = (y - (self.env.size - 1) * 0.5) / (self.env.size - 1)
            for i in range(ord + 1):
                for j in range(i + 1):
                    feature_vector.append(y_normalized ** (ord - i) * x_normalized ** j)

        return np.array(feature_vector)

    def gfv_a(self, fourier: bool, state: int, action: int, ord: int) -> np.ndarray:
        """
        get_feature_vector_with_action
        :param fourier: 是否使用傅里叶特征函数
        :param state: 状态
        :param ord: 特征函数最高阶次数/傅里叶q(对应书)
        :return: 代入state后的计算结果
        """

        if state < 0 or state >= self.state_space_size or action < 0 or action >= self.action_space_size:
            raise ValueError("Invalid state/action value")
        feature_vector = []
        y, x = self.env.state2pos(state) + (1, 1)

        if fourier:
            # 归一化到 -1 到 1
            x_normalized = x / self.env.size
            y_normalized = y / self.env.size
            action_normalized = action / self.action_space_size
            for i in range(ord + 1):
                for j in range(ord + 1):
                    for k in range(ord + 1):
                        feature_vector.append(
                            np.cos(np.pi * (i * x_normalized + j * action_normalized + k * y_normalized)))

        else:
            # 归一化到 0 到 1
            state_normalized = (state - (self.state_space_size - 1) * 0.5) / (self.state_space_size - 1)
            action_normalized = (action - (self.action_space_size - 1) * 0.5) / (self.action_space_size - 1)
            for i in range(ord + 1):
                for j in range(i + 1):
                    feature_vector.append(state_normalized ** (ord - i) * action_normalized ** j)
        return np.array(feature_vector)

    def td_value_approximation(self, learning_rate=0.0005, epochs=100000, fourier=True, ord=5):
        self.state_value=self.policy_evaluation(self.policy)
        if not isinstance(learning_rate, float) or not isinstance(epochs, int) or not isinstance(
                fourier, bool) or not isinstance(ord, int):
            raise TypeError("Invalid input type")
        if learning_rate <= 0 or epochs <= 0 or ord <= 0:
            raise ValueError("Invalid input value")
        episode_length = epochs
        start_state = np.random.randint(self.state_space_size)
        start_action = np.random.choice(np.arange(self.action_space_size),
                                        p=self.mean_policy[start_state])
        episode = self.obtain_episode(self.mean_policy, start_state, start_action, length=episode_length)
        dim = (ord + 1) ** 2 if fourier else np.arange(ord + 2).sum()
        w = np.random.default_rng().normal(size=dim)
        rmse = []
        value_approximation = np.zeros(self.state_space_size)
        for epoch in range(epochs):
            reward = episode[epoch]['reward']
            state = episode[epoch]['state']
            next_state = episode[epoch]['next_state']
            target = reward + self.gama * np.dot(self.gfv(fourier, next_state, ord), w)
            error = target - np.dot(self.gfv(fourier, state, ord), w)
            gradient = self.gfv(fourier, state, ord)
            w = w + learning_rate * error * gradient
            for state in range(self.state_space_size):
                value_approximation[state] = np.dot(self.gfv(fourier, state, ord), w)
            rmse.append(np.sqrt(np.mean((value_approximation - self.state_value) ** 2)))
            print(epoch)
        X, Y = np.meshgrid(np.arange(1, 6), np.arange(1, 6))
        Z = self.state_value.reshape(5, 5)
        Z1 = value_approximation.reshape(5, 5)
        # 绘制 3D 曲面图
        fig = plt.figure(figsize=(8, 6))  # 设置图形的尺寸，宽度为8，高度为6
        ax = fig.add_subplot(121, projection='3d')
        ax.plot_surface(X, Y, Z)
        ax.set_xlabel('X')
        ax.set_ylabel('Y')
        ax.set_zlabel('State Value')
        z_min = -5
        z_max = -2
        ax.set_zlim(z_min, z_max)
        ax1 = fig.add_subplot(122, projection='3d')
        ax1.plot_surface(X, Y, Z1)
        ax1.set_xlabel('X')
        ax1.set_ylabel('Y')
        ax1.set_zlabel('Value Approximation')
        ax1.set_zlim(z_min, z_max)
        fig_rmse = plt.figure(figsize=(8, 6))  # 设置图形的尺寸，宽度为8，高度为6
        ax_rmse = fig_rmse.add_subplot(111)

        # 绘制 rmse 图像
        ax_rmse.plot(rmse)
        ax_rmse.set_title('RMSE')
        ax_rmse.set_xlabel('Epoch')
        ax_rmse.set_ylabel('RMSE')
        plt.show()
        return value_approximation

    def sarsa_function_approximation(self, learning_rate=0.0005, epsilon=0.1, num_episodes=100000, fourier=True, ord=5):
        #BUG

        dim = (ord + 1) ** 2 if fourier else np.arange(ord + 2).sum()
        w = np.random.default_rng().normal(size=dim)

        qvalue_approximation = np.zeros((self.state_space_size, self.action_space_size))
        reward_list = []
        length_list = []
        rmse = []
        policy_rmse = []
        policy = self.mean_policy.copy()
        next_state = 0
        episode = self.obtain_episode(self.mean_policy, 0, 0, length=num_episodes)

        for episode in range(num_episodes):
            # epsilon = (epsilon - 1 / num_episodes) if epsilon > 0 else 0
            done = False
            self.env.reset()
            total_rewards = 0
            episode_length = 0
            while not done:
                state = next_state
                action = np.random.choice(np.arange(self.action_space_size),
                                          p=policy[state])
                _, reward, done, _, _ = self.env.step(action)
                episode_length += 1
                total_rewards += reward
                next_state = self.env.pos2state(self.env.agent_location)
                next_action = np.random.choice(np.arange(self.action_space_size),
                                               p=policy[next_state])
                target = reward + self.gama * np.dot(self.gfv_a(fourier, next_state, next_action, ord), w)
                error = target - np.dot(self.gfv_a(fourier, state, action, ord), w)
                gradient = self.gfv_a(fourier, state, action, ord)
                w = w + learning_rate * error * gradient
                # for state in range(self.state_space_size):
                #     for action in range(self.action_space_size):
                qvalue_approximation[state, action] = np.dot(self.gfv_a(fourier, state, action, ord), w)

                qvalue_star = qvalue_approximation[state].max()
                action_star = qvalue_approximation[state].tolist().index(qvalue_star)
                for a in range(self.action_space_size):
                    if a == action_star:
                        policy[state, a] = 1 - (
                                self.action_space_size - 1) / self.action_space_size * epsilon
                    else:
                        policy[state, a] = 1 / self.action_space_size * epsilon
            rmse.append(np.sqrt(np.mean((qvalue_approximation - self.qvalue) ** 2)))
            # policy_rmse.append(np.sqrt(np.mean((policy - self.policy) ** 2)))
            reward_list.append(total_rewards)
            length_list.append(episode_length)
            print("episode={},length={},reward={}".format(episode, episode_length, total_rewards))

        fig = plt.figure(figsize=(10, 10))
        ax = fig.add_subplot(211)
        ax.plot(reward_list)
        ax.set_ylabel('total_reward')
        ax1 = fig.add_subplot(212)
        ax1.plot(length_list)
        ax1.set_xlabel('episode index')
        ax1.set_ylabel('episode length')
        fig_rmse = plt.figure(figsize=(8, 6))  # 设置图形的尺寸，宽度为8，高度为6
        ax_rmse = fig_rmse.add_subplot(111)
        ax_rmse.plot(rmse, label='qvalue')
        # ax_rmse.plot(policy_rmse,label='policy')

        ax_rmse.set_title('RMSE')
        ax_rmse.set_xlabel('Epoch')
        ax_rmse.set_ylabel('RMSE')
        X, Y = np.meshgrid(np.arange(0, self.action_space_size), np.arange(0, self.state_space_size))
        Z = self.qvalue
        Z1 = qvalue_approximation
        print(Z.shape, Z1.shape, X.shape)

        # 绘制 3D 曲面图
        fig = plt.figure(figsize=(8, 6))  # 设置图形的尺寸，宽度为8，高度为6
        ax = fig.add_subplot(121, projection='3d')
        ax.plot_surface(X, Y, Z)
        ax.set_xlabel('X')
        ax.set_ylabel('Y')
        ax.set_zlabel('q Value')
        # z_min = -5
        # z_max = -2
        # ax.set_zlim(z_min, z_max)
        ax1 = fig.add_subplot(122, projection='3d')
        ax1.plot_surface(X, Y, Z1)
        ax1.set_xlabel('X')
        ax1.set_ylabel('Y')
        ax1.set_zlabel('qValue Approximation')
        fig_rmse = plt.figure(figsize=(8, 6))  # 设置图形的尺寸，宽度为8，高度为6
        ax_rmse = fig_rmse.add_subplot(111)

        plt.show()
        return qvalue_approximation

    def qlearning_function_approximation(self, learning_rate=0.0005, epsilon=0.1, num_episodes=100000, fourier=True,
                                         ord=15):
        #BUG

        dim = (ord + 1) ** 2 if fourier else np.arange(ord + 2).sum()
        w = np.random.default_rng().normal(size=dim)

        qvalue_approximation = np.zeros((self.state_space_size, self.action_space_size))
        reward_list = []
        length_list = []
        rmse = []
        policy = self.mean_policy.copy()
        next_state = 0
        episode = self.obtain_episode(self.mean_policy, 0, 0, length=num_episodes)

        for episode in range(num_episodes):
            # epsilon = (epsilon - 1 / num_episodes) if epsilon > 0 else 0
            done = False
            self.env.reset()
            total_rewards = 0
            episode_length = 0
            while not done:
                state = next_state
                action = np.random.choice(np.arange(self.action_space_size),
                                          p=policy[state])
                _, reward, done, _, _ = self.env.step(action)
                episode_length += 1
                total_rewards += reward
                next_state = self.env.pos2state(self.env.agent_location)
                q_list = []
                for a in range(self.action_space_size):
                    q_list.append(np.dot(self.gfv_a(fourier, next_state, a, ord), w))

                target = reward + self.gama * np.array(q_list).max()
                error = target - np.dot(self.gfv_a(fourier, state, action, ord), w)
                gradient = self.gfv_a(fourier, state, action, ord)
                w = w + learning_rate * error * gradient
                for s in range(self.state_space_size):
                    for a in range(self.action_space_size):
                        qvalue_approximation[s, a] = np.dot(self.gfv_a(fourier, s, a, ord), w)
                qvalue_star = qvalue_approximation[state].max()
                action_star = qvalue_approximation[state].tolist().index(qvalue_star)
                for a in range(self.action_space_size):
                    if a == action_star:
                        policy[state, a] = 1 - (
                                self.action_space_size - 1) / self.action_space_size * epsilon
                    else:
                        policy[state, a] = 1 / self.action_space_size * epsilon
            self.writer.add_scalar('rmse', np.sqrt(np.mean((qvalue_approximation - self.qvalue) ** 2)), episode)
            self.writer.add_scalar('episode_length', episode_length, episode)
            self.writer.add_scalar('total_reward', total_rewards, episode)

            # policy_rmse.append(np.sqrt(np.mean((policy - self.policy) ** 2)))
            # reward_list.append(total_rewards)
            # length_list.append(episode_length)
            print("episode={},length={},reward={}".format(episode, episode_length, total_rewards))

        # fig = plt.figure(figsize=(10, 10))
        # ax = fig.add_subplot(211)
        # ax.plot(reward_list)
        # ax.set_ylabel('total_reward')
        # ax1 = fig.add_subplot(212)
        # ax1.plot(length_list)
        # ax1.set_xlabel('episode index')
        # ax1.set_ylabel('episode length')
        # fig_rmse = plt.figure(figsize=(8, 6))  # 设置图形的尺寸，宽度为8，高度为6
        # ax_rmse = fig_rmse.add_subplot(111)
        # ax_rmse.plot(rmse, label='qvalue')
        # # ax_rmse.plot(policy_rmse,label='policy')
        #
        # ax_rmse.set_title('RMSE')
        # ax_rmse.set_xlabel('Epoch')
        # ax_rmse.set_ylabel('RMSE')
        X, Y = np.meshgrid(np.arange(0, self.action_space_size), np.arange(0, self.state_space_size))
        Z = self.qvalue
        Z1 = qvalue_approximation
        print(Z.shape, Z1.shape, X.shape)

        # 绘制 3D 曲面图
        fig = plt.figure(figsize=(8, 6))  # 设置图形的尺寸，宽度为8，高度为6
        ax = fig.add_subplot(121, projection='3d')
        ax.plot_surface(X, Y, Z)
        ax.set_xlabel('X')
        ax.set_ylabel('Y')
        ax.set_zlabel('q Value')
        z_min = -6
        z_max = 0
        ax.set_zlim(z_min, z_max)
        ax1 = fig.add_subplot(122, projection='3d')
        ax1.plot_surface(X, Y, Z1)
        ax1.set_xlabel('X')
        ax1.set_ylabel('Y')
        ax1.set_zlabel('qValue Approximation')
        ax1.set_zlim(z_min, z_max)

        # fig_rmse = plt.figure(figsize=(8, 6))  # 设置图形的尺寸，宽度为8，高度为6
        # ax_rmse = fig_rmse.add_subplot(111)
        self.writer.close()
        plt.show()
        return qvalue_approximation

    def qvalue_function_approximation(self, learning_rate=0.00008, epsilon=0.1, num_episodes=1000000,
                                      fourier=True,
                                      ord=5):
        #BUG
        dim = (ord + 1) ** 3 if fourier else np.arange(ord + 2).sum()
        w = np.random.default_rng().normal(size=dim)
        qvalue_approximation = np.zeros(shape=(self.state_space_size, self.action_space_size))
        episode = self.obtain_episode(self.mean_policy, 0, 0, length=100000)

        for epoch in range(num_episodes):
            # epsilon = (epsilon - 1 / num_episodes) if epsilon > 0 else 0
            step = int(np.random.randint(low=0, high=99999, size=1))
            reward = episode[step]['reward']
            state = episode[step]['state']
            action = episode[step]['action']
            next_action = episode[step]['next_action']
            next_state = episode[step]['next_state']
            target = reward + self.gama * np.dot(self.gfv_a(fourier, next_state, next_action, ord), w)
            error = target - np.dot(self.gfv_a(fourier, state, action, ord), w)
            gradient = self.gfv_a(fourier, state, action, ord)
            w = w + learning_rate * error * gradient
            for a in range(self.action_space_size):
                qvalue_approximation[state, a] = np.dot(self.gfv_a(fourier, state, a, ord), w)
            self.writer.add_scalar('rmse', np.sqrt(np.mean((qvalue_approximation - self.qvalue) ** 2)), epoch)
            if epoch % 1000 == 0:
                print(epoch, np.sqrt(np.mean((qvalue_approximation - self.qvalue) ** 2)))
        X, Y = np.meshgrid(np.arange(0, self.action_space_size), np.arange(0, self.state_space_size))
        Z = self.qvalue
        Z1 = qvalue_approximation
        print(Z.shape, Z1.shape, X.shape)

        # 绘制 3D 曲面图
        fig = plt.figure(figsize=(8, 6))  # 设置图形的尺寸，宽度为8，高度为6
        ax = fig.add_subplot(121, projection='3d')
        ax.plot_surface(X, Y, Z)
        ax.set_xlabel('X')
        ax.set_ylabel('Y')
        ax.set_zlabel('q Value')
        z_min = -6
        z_max = 0
        ax.set_zlim(z_min, z_max)
        ax1 = fig.add_subplot(122, projection='3d')
        ax1.plot_surface(X, Y, Z1)
        ax1.set_xlabel('X')
        ax1.set_ylabel('Y')
        ax1.set_zlabel('qValue Approximation')
        ax1.set_zlim(z_min, z_max)
        for i in range(self.state_space_size):
            for j in range(self.action_space_size):
                print("qvalue:{},approximation:{}".format(self.qvalue[i, j], qvalue_approximation[i, j]))

        self.writer.close()
        plt.show()
        return qvalue_approximation

    def get_data_iter(self, episode, batch_size=64, is_train=True):
        """构造一个PyTorch数据迭代器"""
        reward = []
        state_action = []
        next_state = []
        for i in range(len(episode)):
            reward.append(episode[i]['reward'])
            action = episode[i]['action']
            y, x = self.env.state2pos(episode[i]['state'])
            state_action.append((y, x, action))
            y, x = self.env.state2pos(episode[i]['next_state'])
            next_state.append((y, x))
        reward = torch.tensor(reward).reshape(-1, 1)
        state_action = torch.tensor(state_action)
        next_state = torch.tensor(next_state)
        data_arrays = (state_action, reward, next_state)
        dataset = data.TensorDataset(*data_arrays)
        return data.DataLoader(dataset, batch_size, shuffle=is_train, drop_last=False)

    def dqn(self, learning_rate=0.0015, episode_length=5000, epochs=600, batch_size=100, update_step=10):
        q_net = QNET()
        policy = self.policy.copy()
        state_value = self.state_value.copy()
        q_target_net = QNET()
        q_target_net.load_state_dict(q_net.state_dict())
        optimizer = torch.optim.SGD(q_net.parameters(),
                                    lr=learning_rate)
        episode = self.obtain_episode(self.mean_policy, 0, 0, length=episode_length)
        date_iter = self.get_data_iter(episode, batch_size)
        loss = torch.nn.MSELoss()
        approximation_q_value = np.zeros(shape=(self.state_space_size, self.action_space_size))
        i = 0
        rmse_list=[]
        loss_list=[]
        for epoch in range(epochs):
            for state_action, reward, next_state in date_iter:
                i += 1
                q_value = q_net(state_action)
                q_value_target = torch.empty((batch_size, 0))  # 定义空的张量
                for action in range(self.action_space_size):
                    s_a = torch.cat((next_state, torch.full((batch_size, 1), action)), dim=1)
                    q_value_target = torch.cat((q_value_target, q_target_net(s_a)), dim=1)
                q_star = torch.max(q_value_target, dim=1, keepdim=True)[0]
                y_target_value = reward + self.gama * q_star
                l = loss(q_value, y_target_value)
                optimizer.zero_grad()  # PyTorch中默认梯度会累积,这里需要显式将梯度置为0S
                l.backward()  # 反向传播更新参数
                optimizer.step()
                if i % update_step == 0 and i != 0:
                    q_target_net.load_state_dict(
                        q_net.state_dict())  # 更新目标网络
                    # policy = np.zeros(shape=(self.state_space_size, self.action_space_size))
            loss_list.append(float(l))
            print("loss:{},epoch:{}".format(l, epoch))
            self.policy = np.zeros(shape=(self.state_space_size, self.action_space_size))
            self.state_value = np.zeros(shape=self.state_space_size)

            for s in range(self.state_space_size):
                y, x = self.env.state2pos(s)
                for a in range(self.action_space_size):
                    approximation_q_value[s, a] = float(q_net(torch.tensor((y, x, a)).reshape(-1, 3)))
                q_star_index = approximation_q_value[s].argmax()
                self.policy[s, q_star_index] = 1
                self.state_value[s] = approximation_q_value[s, q_star_index]
            rmse_list.append(np.sqrt(np.mean((state_value - self.state_value) ** 2)))
            # policy_rmse = np.sqrt(np.mean((policy - self.policy) ** 2))
        fig_rmse = plt.figure(figsize=(8, 12))  # 设置图形的尺寸，宽度为8，高度为6
        ax_rmse = fig_rmse.add_subplot(211)

        # 绘制 rmse 图像
        ax_rmse.plot(rmse_list)
        ax_rmse.set_title('RMSE')
        ax_rmse.set_xlabel('Epoch')
        ax_rmse.set_ylabel('RMSE')
        self.writer.close()
        ax_loss = fig_rmse.add_subplot(212)

        ax_loss.plot(loss_list)
        ax_loss.set_title('loss')
        ax_loss.set_xlabel('Epoch')
        ax_loss.set_ylabel('Loss')
        plt.show()

    def obtain_episode_p(self, policy_net, start_state, start_action):
        f"""

        :param policy_net: 由指定策略产生episode
        :param start_state: 起始state
        :param start_action: 起始action
        :return: 一个 state,action,reward,next_state,next_action 序列
        """
        self.env.agent_location = self.env.state2pos(start_state)
        episode = []
        next_action = start_action
        next_state = start_state
        done = False
        while not done:
            state = next_state
            action = next_action
            _, reward, done, _, _ = self.env.step(action)
            next_state = self.env.pos2state(self.env.agent_location)
            y, x = self.env.state2pos(next_state) / self.env.size
            prb = policy_net(torch.tensor((y, x)).reshape(-1, 2))[0]

            next_action = np.random.choice(np.arange(self.action_space_size),
                                           p=prb.detach().numpy())
            episode.append({"state": state, "action": action, "reward": reward, "next_state": next_state,
                            "next_action": next_action})
        return episode