强化学习理论-第4课-值迭代与策略迭代

1. value iteration algorithm:

值迭代上一节已经介绍过：

1.1 policy update:

1.2 Value update：

此时，\(\pi_{k+1}\)和\(v_k\)都是已知的

1.3 procedure summary：

1.4 example:

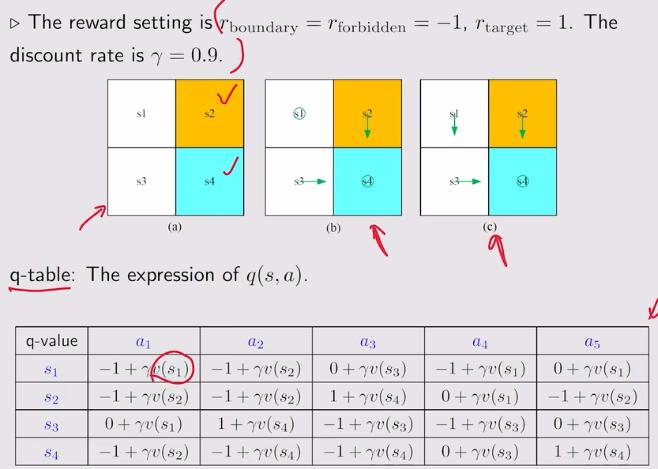
2. policy iteration algorithm:

Q1:

Q2:

Q3:

2.1 Policy evaluation:

2.2 Policy improvement:

3. truncated policy iteration algorithm

3.1 compare value iteration and policy iteration:

计算一步是value interation，计算无穷多步，就是policy iteration。中间截断一步，就叫做truncated policy iteration

3.2 pseudocode：

4. summary:

def random_greed_policy(self):
        """
        生成随机的greedy策略
        :return:
        """
        policy = np.zeros(shape=(self.state_space_size, self.action_space_size))
        for state_index in range(self.state_space_size):
            action = np.random.choice(range(self.action_space_size))
            policy[state_index, action] = 1
        return policy

    def policy_evaluation(self, policy, tolerance=0.001, steps=10):
        """
        迭代求解贝尔曼公式 得到 state value tolerance 和 steps 满足其一即可
        :param policy: 需要求解的policy
        :param tolerance: 当 前后 state_value 的范数小于tolerance 则认为state_value 已经收敛
        :param steps: 当迭代次数大于step时 停止计算 此时若是policy iteration 则算法变为 truncated iteration
        :return: 求解之后的收敛值
        """
        state_value_k = np.ones(self.state_space_size)
        state_value = np.zeros(self.state_space_size)
        while np.linalg.norm(state_value_k - state_value, ord=1) > tolerance:
            state_value = state_value_k.copy()
            for state in range(self.state_space_size):
                value = 0
                for action in range(self.action_space_size):
                    value += policy[state, action] * self.calculate_qvalue(state_value=state_value_k.copy(),
                                                                           state=state,
                                                                           action=action)  # bootstrapping
                state_value_k[state] = value
        return state_value_k

    def policy_improvement(self, state_value):
        """
        是普通 policy_improvement 的变种 相当于是值迭代算法 也可以 供策略迭代使用 做策略迭代时不需要 接收第二个返回值
        更新 qvalue ；qvalue[state,action]=reward+value[next_state]
        找到 state 处的 action*：action* = arg max(qvalue[state,action]) 即最优action即最大qvalue对应的action
        更新 policy ：将 action*的概率设为1 其他action的概率设为0 这是一个greedy policy
        :param: state_value: policy对应的state value
        :return: improved policy, 以及迭代下一步的state_value
        """
        policy = np.zeros(shape=(self.state_space_size, self.action_space_size))
        state_value_k = state_value.copy()
        for state in range(self.state_space_size):
            qvalue_list = []
            for action in range(self.action_space_size):
                qvalue_list.append(self.calculate_qvalue(state, action, state_value.copy()))
            state_value_k[state] = max(qvalue_list)
            action_star = qvalue_list.index(max(qvalue_list))
            policy[state, action_star] = 1
        return policy, state_value_k

    def calculate_qvalue(self, state, action, state_value):
        """
        计算qvalue elementwise形式
        :param state: 对应的state
        :param action: 对应的action
        :param state_value: 状态值
        :return: 计算出的结果
        """    
        qvalue = 0
        for i in range(self.reward_space_size):
            qvalue += self.reward_list[i] * self.env.Rsa[state, action, i]
        for next_state in range(self.state_space_size):
            qvalue += self.gama * self.env.Psa[state, action, next_state] * state_value[next_state]
        return qvalue

    def value_iteration(self, tolerance=0.001, steps=100):
        """
        迭代求解最优贝尔曼公式 得到 最优state value tolerance 和 steps 满足其一即可
        :param tolerance: 当 前后 state_value 的范数小于tolerance 则认为state_value 已经收敛
        :param steps: 当迭代次数大于step时 停止 建议将此变量设置大一些
        :return: 剩余迭代次数
        """
        state_value_k = np.ones(self.state_space_size)
        while np.linalg.norm(state_value_k - self.state_value, ord=1) > tolerance and steps > 0:
            steps -= 1
            self.state_value = state_value_k.copy()
            self.policy, state_value_k = self.policy_improvement(state_value_k.copy())
        return steps

    def policy_iteration(self, tolerance=0.001, steps=100):
        """

        :param tolerance: 迭代前后policy的范数小于tolerance 则认为已经收敛
        :param steps: step 小的时候就退化成了  truncated iteration
        :return: 剩余迭代次数
        """
        policy = self.random_greed_policy()
        while np.linalg.norm(policy - self.policy, ord=1) > tolerance and steps > 0:
            steps -= 1
            policy = self.policy.copy()
            self.state_value = self.policy_evaluation(self.policy.copy(), tolerance, steps)
            self.policy, _ = self.policy_improvement(self.state_value)
        return steps