四足机器人MPC+WBC方案
四足机器人MPC+WBC方案
一、MPC:
系统方程:
状态变量:\(x_r = (h_{com}, q_b, q_j) \in R^{24}\), 包含6维质心点动量,6维机身位姿,3*4个关节角度
输入变量:\(u = (f_{c1}, ......, f_{c4}, v_j) \in R^{3*4+12}\), 包含4个腿末端的3维力,12个关节速度
动力学:
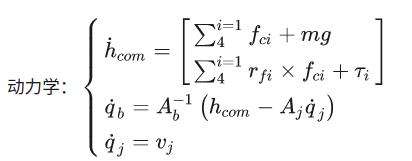
其中\(f_{ci}\)是4足末端的接触力,\(r_{fi}\)是足触地相对于质心的位置矢量, \(h_{com}\)是质心动量,A是质心动力学的刚体惯性矩阵
动量=mv;所以
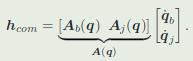
动量求导后,变成ma,就是力。
cost function:
- 机体跟随误差(姿态,位置,角速度,速度)
- 足轨迹跟随误差(关节角,关节角速度,接触脚在世界坐标系下的位置和速度,接触力)
- 关节速度和接触力中的高频内容惩罚
- relaxed barrier functions 不等式约束
机体误差和足迹轨迹误差:
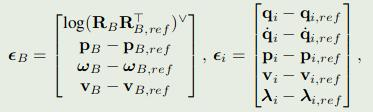
relaxed barrier functions 不等式约束:
-
relaxed barrier functions:
![]()
-
全惩罚项:
![]()
-
关节角、角速度、关节力矩上下限:
![]()
-
落足区域:
![]()
-
摩擦锥约束:
![]()
-
障碍物约束:
![]()
等式约束:
- \(f_{ci} = 0\) 摆动腿的接触力为0
- \(v_{ci} = 0\) 支撑腿的接触速度为0
- \(v_{ci}n_z = v^{*}_z\) 对于摆动相,参考轨迹仅在地表法线方向约束(这样即保证了足部以指定的速度抬离并离地,同时又在切线方向有足够的灵活度)
二、WBC:
坐标系:
I:惯性坐标系,世界坐标系?
B:自由浮动基座,baselink?
C:地面坐标系,x,y方向和B坐标系相同,Z坐标系垂直于地形
2.1 模型:
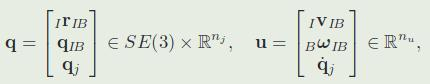
\(n_u = 6 + n_j\),6+12=18
系统方程:
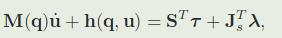
\(M(q) \in R^{n_u * n_u}\):质量矩阵
\(h(q,u) \in R^{n_u}\):科里奥利力、离心力、重力项
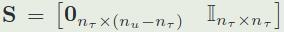
如果所有的关节都能驱动,\(n_{\tau} = n_j\),也就是12
\(J_s \in R^{3n_c * n_u}\):堆叠约束雅可比,\(J_s = [J^T_{C_1} ...... J^T_{C_{nc}}]\)
\(n_c\)是接触点数量,正常是4个
支撑接触点的运动约束:
将脚建模为点接触,\(r_{IC}\)是力,支撑的时候,是静止的,所以速度和加速度为0
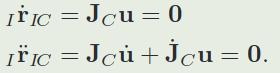
支撑一致性动力学:
如果运动保持在上诉的接触约束的零空间中,动力学方程可以投影到缩减空间动力学,通过QR分解得到支撑雅可比
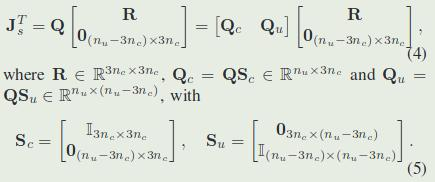
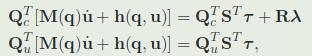
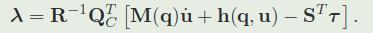
2.2 零空间:
任务定义:
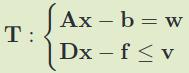
零空间定义:
\(Z_p = N(\underline{A}_p)\), \(\underline{A}_p\)是多任务A的集合
\(x = s^{*} + Z_p z_{p+1}\),\(z_{p+1}\)是行空间\(Z_p\)的一个向量
求解一个新的任务\(T_{p+1}\),意味着求解\(z^{*}_{p+1}\)和\(v^{*}_{p+1}\)

\(Z_p\)是任务堆叠矩阵A的零空间,可以用QR或SVD分解得。
任务很多的时候,可以使用迭代求解零空间:

stackedZ_ = stackedZPrev_ * (task_.a_ * stackedZPrev_).fullPivLu().kernel();
2.3 多任务:
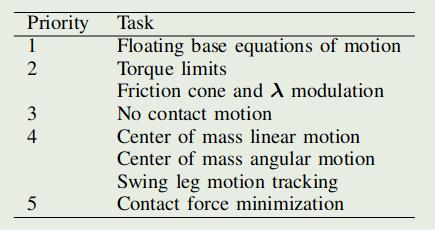
1. 等式任务:
- 浮动基座系统方程:
\([M_{fb} -J^{T}_{s_{fb}} ] \xi_d = -h_{fb}\)
\(M_{fb},J^{T}_{s_{fb}}, h_{fb}\)分别是惯性矩阵的前6行(关于6自由度基座相关),基座的雅可比,非线性项
\(\xi_d = [\dot{u}^{T}_{d}, \lambda^T_d]^T \in R^{n_u+n_c}\),关节加速度和接触力
Task WbcBase::formulateFloatingBaseEomTask() {
auto& data = pinocchioInterfaceMeasured_.getData();
matrix_t s(info_.actuatedDofNum, info_.generalizedCoordinatesNum);
s.block(0, 0, info_.actuatedDofNum, 6).setZero();
s.block(0, 6, info_.actuatedDofNum, info_.actuatedDofNum).setIdentity();
matrix_t a = (matrix_t(info_.generalizedCoordinatesNum, numDecisionVars_) << data.M, -j_.transpose(), -s.transpose()).finished();
vector_t b = -data.nle;
return {a, b, matrix_t(), vector_t()};
}
- 运动等式约束:
只要运动在接触零空间内,接触力就可以表示为扭矩和产生运动的线性组合,在运动空间和扭矩空间寻找解:
\(x_d = [\dot{u}^{T}_{d}, \tau^T_d]^T\)
运动等式方程:
\(Q^T_u [-M(q),S^T]x_d = Q^T_u h(q,u)\)
- 接触运动约束:
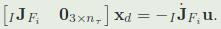
摆动腿从腾空状态过度到触地状态后,为防止足端继续移动,需要保证足端的速度为零
Task WbcBase::formulateNoContactMotionTask() {
matrix_t a(3 * numContacts_, numDecisionVars_);
vector_t b(a.rows());
a.setZero();
b.setZero();
size_t j = 0;
for (size_t i = 0; i < info_.numThreeDofContacts; i++) {
if (contactFlag_[i]) {
a.block(3 * j, 0, 3, info_.generalizedCoordinatesNum) = j_.block(3 * i, 0, 3, info_.generalizedCoordinatesNum);
b.segment(3 * j, 3) = -dj_.block(3 * i, 0, 3, info_.generalizedCoordinatesNum) * vMeasured_;
j++;
}
}
return {a, b, matrix_t(), vector_t()};
}
- 质心轨迹跟踪:
由MPC得到质心期望位置、速度、加速度,分别为\(p^{des}_{com}, \dot{p}^{des}_{com}, \ddot{p}^{des}_{com}\)
由\(\ddot{p}^{des}_{com} = \ddot{p}_{com} + K_p e_{com} + K_d \dot{e}_{com}\)
得:\([J_{com}, 0_{6*36}] x_d = \ddot{p}_{com} + K_p e_{com} + K_d \dot{e}_{com} - \dot{J}_{com} \dot{q}\)
其中\(e_{com}\)是位置误差,\(\dot{e}_{com}\)是速度误差。
- 足端轨迹跟踪:
足端定义五次Hermite splines曲线,提供期望位置,速度和加速度在坐标系C中。
\([J_{ci}, 0_{3*39}] x_d = \ddot{p}_{ci} + K_p e_{ci} + K_d \dot{e}_{ci} - \dot{J}_{ci} \dot{q}\)
Task WbcBase::formulateSwingLegTask() {
eeKinematics_->setPinocchioInterface(pinocchioInterfaceMeasured_);
std::vector<vector3_t> posMeasured = eeKinematics_->getPosition(vector_t());
std::vector<vector3_t> velMeasured = eeKinematics_->getVelocity(vector_t(), vector_t());
eeKinematics_->setPinocchioInterface(pinocchioInterfaceDesired_);
std::vector<vector3_t> posDesired = eeKinematics_->getPosition(vector_t());
std::vector<vector3_t> velDesired = eeKinematics_->getVelocity(vector_t(), vector_t());
matrix_t a(3 * (info_.numThreeDofContacts - numContacts_), numDecisionVars_);
vector_t b(a.rows());
a.setZero();
b.setZero();
size_t j = 0;
for (size_t i = 0; i < info_.numThreeDofContacts; ++i) {
if (!contactFlag_[i]) {
vector3_t accel = swingKp_ * (posDesired[i] - posMeasured[i]) + swingKd_ * (velDesired[i] - velMeasured[i]);
a.block(3 * j, 0, 3, info_.generalizedCoordinatesNum) = j_.block(3 * i, 0, 3, info_.generalizedCoordinatesNum);
b.segment(3 * j, 3) = accel - dj_.block(3 * i, 0, 3, info_.generalizedCoordinatesNum) * vMeasured_;
j++;
}
}
return {a, b, matrix_t(), vector_t()};
}
2. 不等式任务:
- 力矩限制:
\(\begin{bmatrix} 0_{12*18} & E_{12*12} & 0_{12*12} \\ 0_{12*18} & -E_{12*12} & 0_{12*12} \\ \end{bmatrix} x_d <= \begin{bmatrix} \tau^{max}_{12*1} \\ -\tau ^{min}_{12*1} \\ \end{bmatrix}\)
Task WbcBase::formulateTorqueLimitsTask() {
matrix_t d(2 * info_.actuatedDofNum, numDecisionVars_);
d.setZero();
matrix_t i = matrix_t::Identity(info_.actuatedDofNum, info_.actuatedDofNum);
d.block(0, info_.generalizedCoordinatesNum + 3 * info_.numThreeDofContacts, info_.actuatedDofNum, info_.actuatedDofNum) = i;
d.block(info_.actuatedDofNum, info_.generalizedCoordinatesNum + 3 * info_.numThreeDofContacts, info_.actuatedDofNum,
info_.actuatedDofNum) = -i;
vector_t f(2 * info_.actuatedDofNum);
for (size_t l = 0; l < 2 * info_.actuatedDofNum / 3; ++l) {
f.segment<3>(3 * l) = torqueLimits_;
}
return {matrix_t(), vector_t(), d, f};
}
- 足端作用力限制:
足端z轴方向的作用力需大于零,并且x和y轴方向牵引力要小于摩擦力。其中\(S^1_{12*1}\)和\(S^2_{12*12}\)为选择矩阵,选择触地足端作用力;
\(f^1_{12*1}\)和\(f^2_{12*1}\)表示各方向摩擦力的上限和下限。
\(\begin{bmatrix} 0_{12*18} & 0_{12*12} & S^1_{12*12} \\ 0_{12*18} & 0_{12*12} & -S^2_{12*12} \\ \end{bmatrix} x_d <= \begin{bmatrix} u * f^1_{12*1} \\ -u * f^2_{12*1} \\ \end{bmatrix}\)
Task WbcBase::formulateFrictionConeTask() {
matrix_t a(3 * (info_.numThreeDofContacts - numContacts_), numDecisionVars_);
a.setZero();
size_t j = 0;
for (size_t i = 0; i < info_.numThreeDofContacts; ++i) {
if (!contactFlag_[i]) {
a.block(3 * j++, info_.generalizedCoordinatesNum + 3 * i, 3, 3) = matrix_t::Identity(3, 3);
}
}
vector_t b(a.rows());
b.setZero();
matrix_t frictionPyramic(5, 3); // clang-format off
frictionPyramic << 0, 0, -1,
1, 0, -frictionCoeff_,
-1, 0, -frictionCoeff_,
0, 1, -frictionCoeff_,
0,-1, -frictionCoeff_; // clang-format on
matrix_t d(5 * numContacts_ + 3 * (info_.numThreeDofContacts - numContacts_), numDecisionVars_);
d.setZero();
j = 0;
for (size_t i = 0; i < info_.numThreeDofContacts; ++i) {
if (contactFlag_[i]) {
d.block(5 * j++, info_.generalizedCoordinatesNum + 3 * i, 5, 3) = frictionPyramic;
}
}
vector_t f = Eigen::VectorXd::Zero(d.rows());
return {a, b, d, f};
}


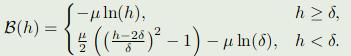

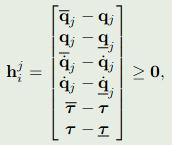
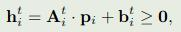

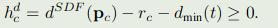

 浙公网安备 33010602011771号
浙公网安备 33010602011771号