数据结构期末复习
前言:
第一次接触数据结构时,我觉得这门课特别抽象,和无聊。抽象在于,第一次接触就被一些没怎么名词,线性表,链表,队列,栈,散列表 这些奇怪的词语弄迷糊了,我一直很好奇,
这些名字真的能帮我们理解这个数据结构吗?
一、数据结构:
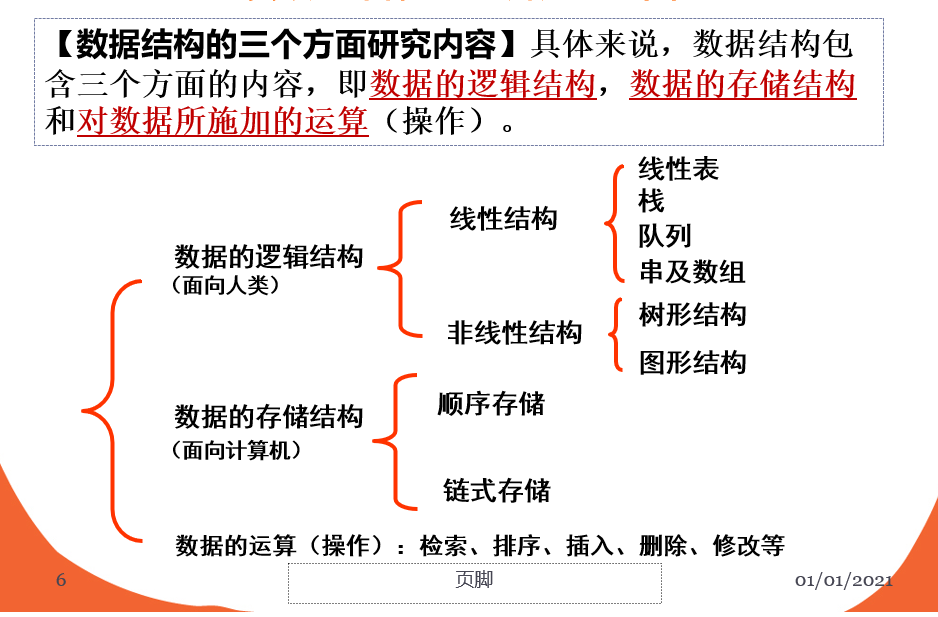

其中,图和树不用多说,集合这样的类型,典型的数据结构就是集合,其次 并查集。 这样的逻辑结构的特点是:元素之间的共性仅仅是属于一个集合而已。
物理储存方式:


这个秒啊,插不到前面去,就插他后面,然后把数据交换。
我的思路:遍历链表,全部反转一遍。然后从尾往头遍历n个长度。
二、队列
参考:https://www.jianshu.com/p/9ba8a65464dd
结论:
0.普通队列,插入元素rear 指针后移,删除元素,front指针后移。 队列满条件:rear 超过数组下标。
1.为了解决假溢出,使用循环队列。
2.循环队列中,插入元素的下一位置为 (rear+1)% maxsize
3.循环队列队满条件也是rear=front
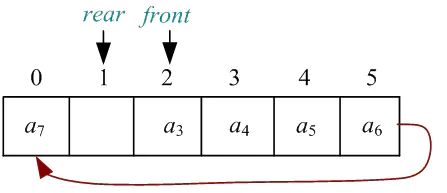
(Q.rear+1) %Maxsize= Q.front,此时为队满。
队空:Q.front=Q.rear; // Q.rear和Q.front指向同一个位置
队满: (Q.rear+1) %Maxsize=Q.front; // Q.rear向后移一位正好是Q.front
入队:
Q.base[Q.rear]=x; //将元素放入Q.rear所指空间,
Q.rear =( Q.rear+1) %Maxsize; // Q.rear向后移一位
出队:
e= Q.base[Q.front]; //用变量记录Q.front所指元素,
Q.front=(Q.front+1) %Maxsize // Q. front向后移一位
三、二叉树
分类:
基本结论:

3、 三种遍历
preorder:中 左 右
inorder: 左 中 右
postorder: 左 右 中
根据遍历方式 确定二叉树,必须要有中序+其他一个
4.森林与二叉树的转换
1、树转换为二叉树 :孩子兄弟表示法
任何一颗树都是二叉树。
左节点 连接兄弟
保留父节点和左孩子的连线,删除与其他孩子的连线。
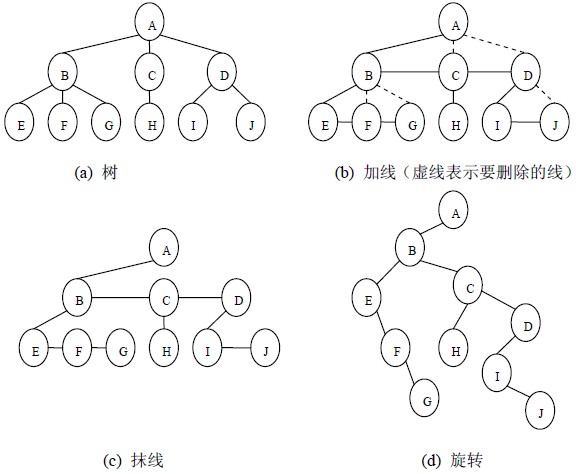
旋转。
(1)加线。就是在所有兄弟结点之间加一条连线;
(2)抹线。就是对树中的每个结点,只保留他与第一个孩子结点之间的连线,删除它与其它孩子结点之间的连线;
(3)旋转。就是以树的根结点为轴心,将整棵树顺时针旋转一定角度,使之结构层次分明。
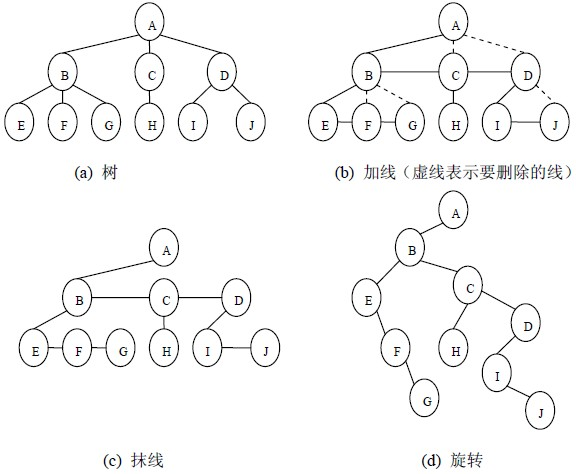
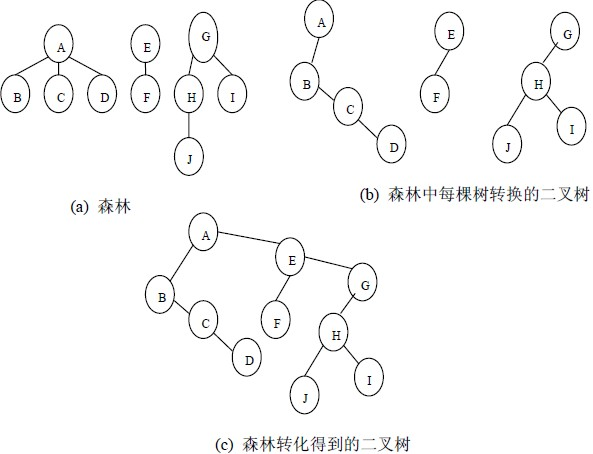
森林转换为二叉树:
首先,啥是森林?
树的集合。
如图,三棵树集合在一起,组成为一个森林。
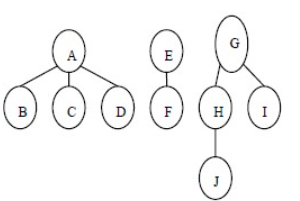
转换步骤:
1.把每棵树变成二叉树
2.从第二棵树开始,根节点连接前一颗树的右孩子。
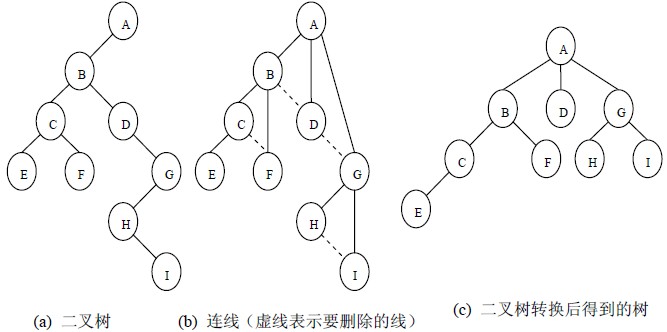
二叉树转化为树:
这就是树变二叉树的逆过程。即孩子兄弟表示法的逆过程。
我们知道,树变二叉树的过程中,树上的一个节点,与他左边第一个孩子保持关系,剩下的孩子都成了第一个孩子的右边一顺溜。
所以拿到一个二叉树,就把他左孩子的右边一顺溜,全部和他连起来。这就是他的孩子。
二叉树转换为树是树转换为二叉树的逆过程,其步骤是:
(1)若某结点的左孩子结点存在,将左孩子结点的右孩子结点、右孩子结点的右孩子结点……都作为该结点的孩子结点,将该结点与这些右孩子结点用线连接起来;
(2)删除原二叉树中所有结点与其右孩子结点的连线;
(3)整理(1)和(2)两步得到的树,使之结构层次分明。
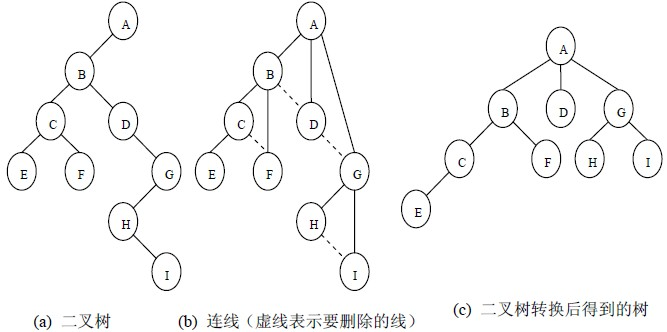
图:

1.DFS:
从一个点出发,一直往第一个邻接点的方向走,如果走到一个邻接点都被遍历过的点,回退到上一个点,直到最开始的点的邻接点都被遍历完成。
2.BFS:


prim:
一颗小树快快长大。
1。选取初始点v,放入minimal spanning tree的集合,作为生成树的一个节点。
2. 遍历他的邻接点w,更新邻接点到最小生成树的距离。(即 该距离dist=min(dist, edge length (v,w))))
Kruskal算法:
小树合并成森林。
先把所有顶点都看成一颗最小生成树,然后将它们合并起来就可了。
维护一个最小生成树的边集合。
只要我们取的边数没有到N-1条,并且图上还有边给我们取
我们就取出一条权重最小的边,然后把这条边从图上删除。
看看这条边是否构成回路,如果不构成回路,就加入到最小生成树的边集里。
循环出来后,判断边数是否为N-1 不是则说明图不连通,无最小生成树。
拓扑排序:
条件.有向无环图。
流程:
1.遍历所有节点,找到入度为0的节点入队。
2.弹出入度为0的节点,后遍历这个节点的邻接点,把他们的入度-1,如果为0,再放入队列中。
3.循环跳出后,还有节点没有被遍历到说明图不是有向无环图。return Error
查找表:
1.分类:
静态查找, 操作完成后表不改变
动态查找, 表改变
2. 平均查找长度:
期望值。
ASL=sum(pi*ci)
ci 找i个记录需要的比较次数
pi i个记录出现的概率 1/n
哨兵: 让0下标位置放要查找的元素,查找时间节约一半。
3. 二叉排序树
4.二分搜索
排序:
1.插入排序:
1) 抽一张牌q,放入手牌中(手牌都是有序的)
2) 再抽一张n,比较大小,插在手牌里合适的位置。(比左边大,比右边小)
2.冒泡排序:
1)从起始位置开始,依次比较相邻两元素的大小,如果逆序,则交换。
2)比较完成后,n-i个位置是第n-i 大的元素。
总结:
这两种排序都是交换顺序的排序,逆序对有多少个就需要交换多少次,
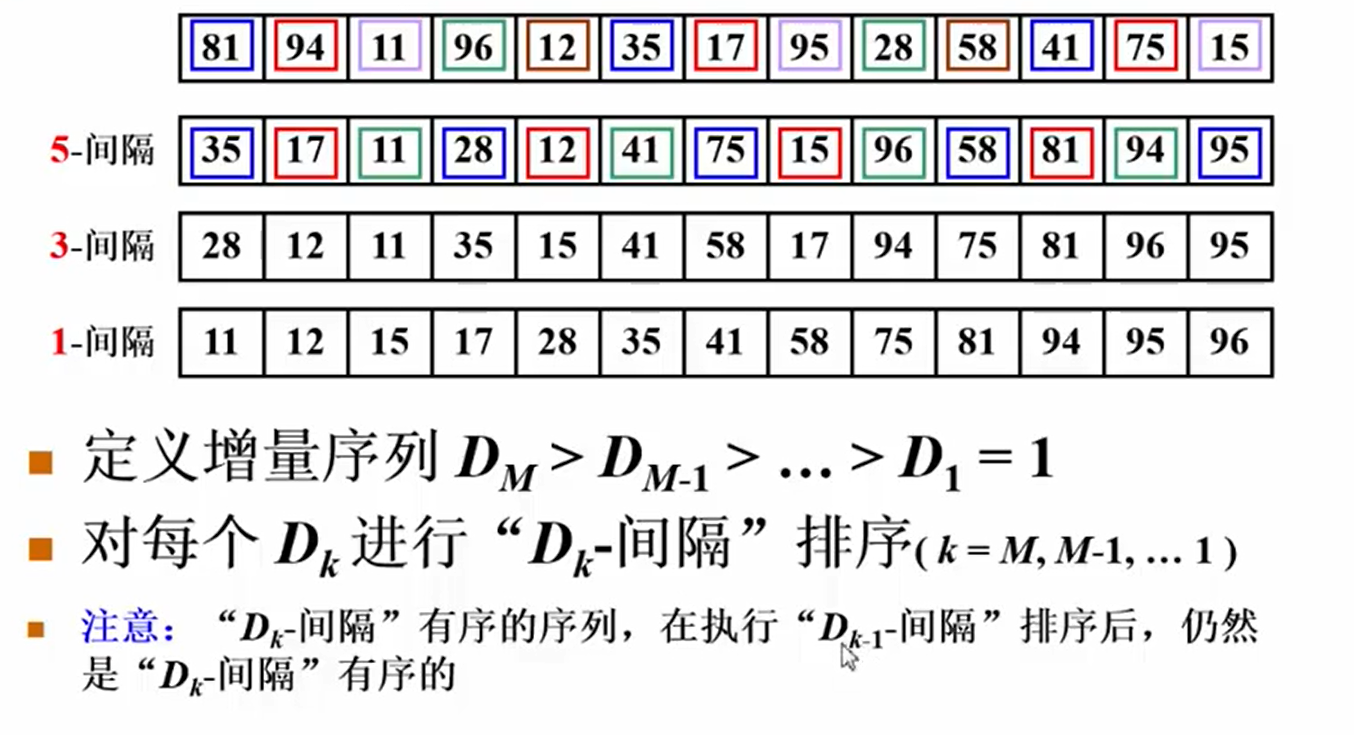
3.希尔排序
1) 每个d个间隔取出元素来,做插入排序。
2) d 减小,重复1)
3) 直到d=1,做完全的插入排序。
前面1) 2)的步骤是为3)做铺垫,消除绝大多数有序对。
3.选择排序:
每次从无序序列中选择出一个最小元,和有序部分的最后一个元素交换。
找到最小元的方法有:
1). 遍历寻找 O(n)
2.) 堆排序
4.堆排序:
方法1:
1.)建堆
2) 堆中弹出元素 赋值给数组
额外空间复杂度O(n)
方法2:
1) 建堆
2) 交换堆顶和第i个元素的位置
3) 从第i个元素往上建堆。
以上是O(n^2)复杂度的排序。
---------------------------------------------------------------
以下是O(n*logn)复杂度的排序。 两种递归的排序方式。
1.归并排序:
1) 递归把序列分成不可再分的若干小序列。(递归)
2) 将各个小序列 归并为有序 序列
3) 返回上一层,直至整体序列有序。
https://pic4.zhimg.com/v2-a29c0dd0186d1f8cef3c5ebdedf3e5a3_b.webp

额外空间复杂度是O(n)
2. 快速排序:
1) 选出一个pivot 元素作为基准,通过交换元素的方式将左右两边调整为左边元素都比pivot 小,右边元素都比pivot 大。
2) 递归左半边和右半边。
void quick_sort(int q[], int l, int r)
{
if (l >= r) return;
int i = l - 1, j = r + 1, x = q[l + r >> 1];
while (i < j)
{
do i ++ ; while (q[i] < x);
do j -- ; while (q[j] > x);
if (i < j) swap(q[i], q[j]);
}
quick_sort(q, l, j), quick_sort(q, j + 1, r);
}
作者:yxc
链接:https://www.acwing.com/blog/content/277/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
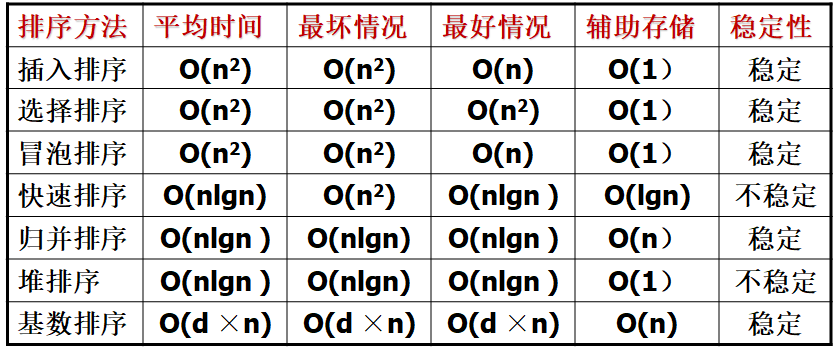
关于排序的稳定性:
链接:https://www.nowcoder.com/questionTerminal/38bb6a80673b4052a79b6932e4fee5c1?toCommentId=1998023
来源:牛客网
例题: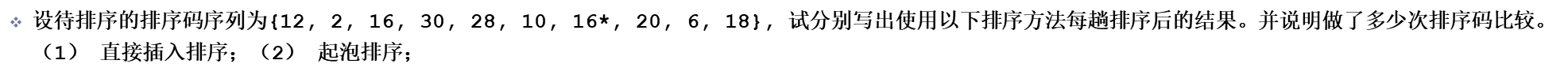
使用以上的排序方式。
二叉搜索树:
堆:
取出元素的顺序按照元素的优先级。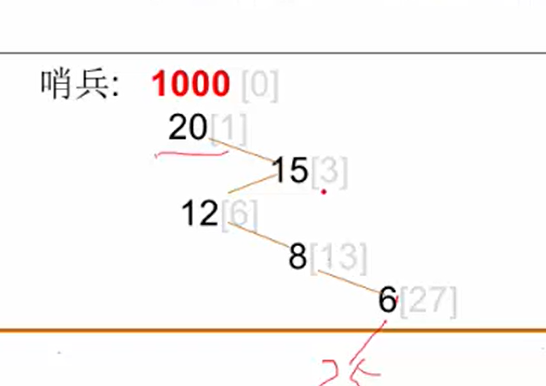
3)删除: 删除的位置是确定的,肯定是根节点。
删除根节点后,将最后一个元素补到根节点位置上,
再调整堆的结构(比较根节点元素和它左右孩子的最大值,如果不满足,交换),使它满足性质。
4) 建堆:
链接:https://www.nowcoder.com/questionTerminal/1f1d7f05826140eaaccf534892758753
来源:牛客网
- 首先根据序列构建一个完全二叉树
- 在完全二叉树的基础上,从最后一个非叶结点开始调整:比较三个元素的大小–自己,它的左孩子,右孩子。分为三种情况:
- 自己最小,不用调整
- 左孩子最小,交换该非叶结点与其左孩子的值,并考察以左孩子为根的子树是否满足小顶堆的要求,不满足递归向下处理
- 右孩子最小,交换该非叶结点与其右孩子的值,并考察以右孩子为根的子树是否满足小顶堆的要求,不满足递归向下处理
二叉搜索树:
左子树都比根节点小,右子树都比根节点大。
1) 插入: 不论如何插入的节点都会变成叶子节点。 所以只需要查找到要插入的位置,然后插入即可。
2) 删除: 若删除叶节点,则直接删除。若非叶子节点,则删除后将左子树的最大值(左子树的最右边节点)补在根节点位置或者右子树的最小值(右子树的最左边节点)。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号