秒懂拓扑排序

Intorduction：

拓扑排序和普通排序不同，拓扑排序是专门为了解决特定的排序问题。如：排课问题。

在现实生活中，我们往往需要先学一门课，有这门课的基础才能学下一门。比如学了小学数学才能学中学数学，学了中学数学才能学高数。学了c语言才能学c++ 等等。

要学一门课就必须要学这门课的先修课。当然这门课也会构成你后面要学课的先修课。

那么，如何找到一个正确的学习顺序？ 这时候就需要用到拓扑排序。当然了，使用拓扑排序之前还需要把这些不同的课，课与课之间的关系抽象成图。

 

 

 

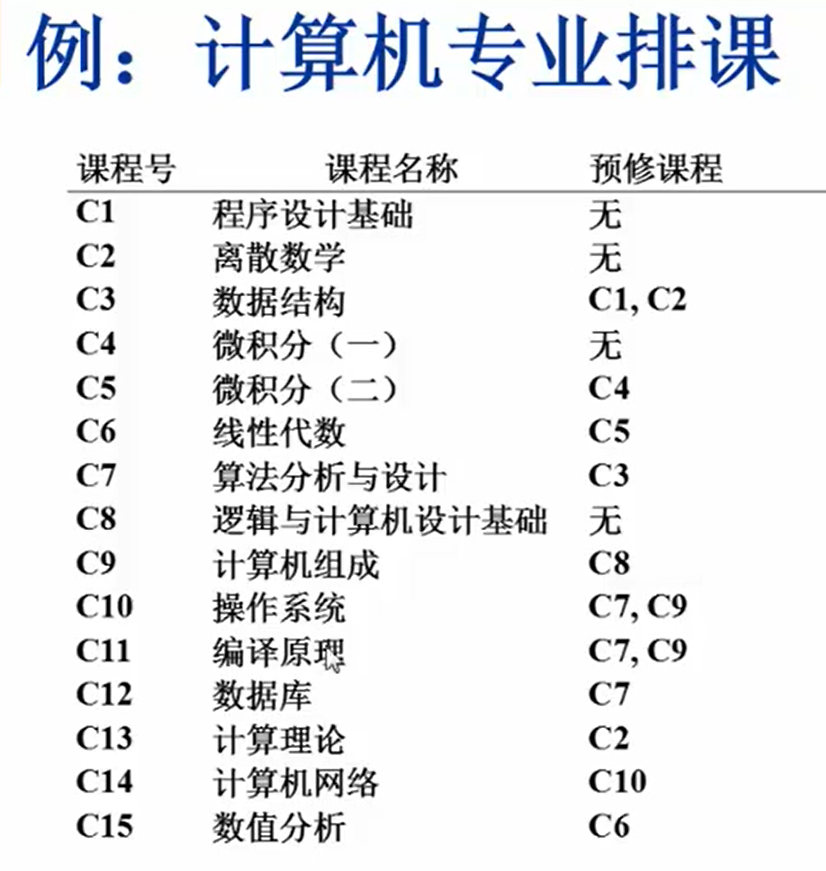
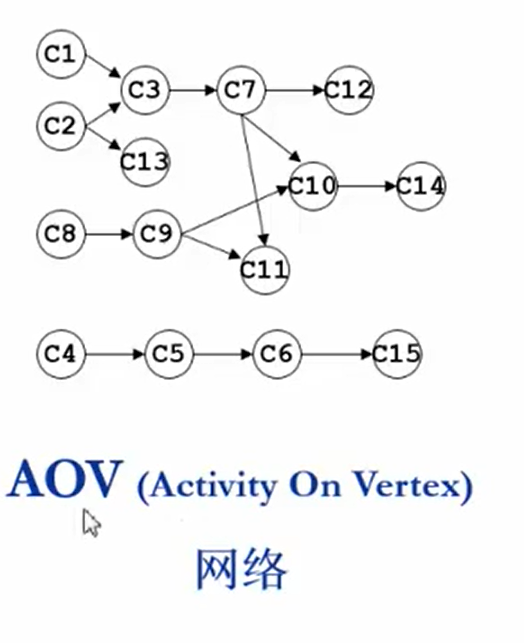
什么样的图有拓扑序呢？

必须是有向无环图。

Why？ 试想一下，如果无向就不存在先后顺序了，如果有环意味着这个节点就是这个节点的先驱节点（也就是这门课就是自己的先修课），不符合逻辑。

算法流程：

先推理一下，我们要排课，首先要排什么课？

肯定是没有预修课程的课了。对应成图上的节点就是入度为0的课，没有其他课指向的课。

把这个节点放在排序的最前面，意味着这门课已经被学完了，那对于这张图上的其他课来说（其他节点），你已经有了这门课的基础，那是不是可以把这门课的节点指向其他课节点W 的边去掉，因为这样去掉，意味着学W课程不需要预修课程，这样也是逻辑合理的，因为我们已经学过了W的预修课程，就可以把W看成不需要预修课程的了。

去掉这些边后，又可以在图上找入度为0的节点，重复即可。

简化一下：

1.遍历所有节点，找到入度为0的节点入队。

2.弹出入度为0的节点，后遍历这个节点的邻接点，把他们的入度-1，如果为0，再放入队列中。

3.循环跳出后，还有节点没有被遍历到说明图不是有向无环图。Error

 

代码：

list<Node*> sortedTopology(Graph& graph) {
    queue<Node*> zeroDegree;  // queue contains nodes that in degree is zero 
    unordered_map<Node*, int> inDegree;  // container collects in degree of all the node in graph
    unordered_map<int, Node*>::iterator ite = graph.nodes.begin(); // iterator for while loop
    list<Node*> ret; // return value
    int cnt = 0; // count if all the nodes are traversed.
    while (ite!=graph.nodes.end()) {
        // traverse all the node find out which node has zero in degree and push it into queue.

        inDegree[ite->second] = ite->second->in;
        if (ite->second->in == 0) {
            zeroDegree.push(ite->second);
        }
        ite++;
        
    }

    while (!zeroDegree.empty()) {
        Node* temp=zeroDegree.front();
        zeroDegree.pop();
        cnt++;
        ret.push_back(temp);
        // pop one
        for (auto node : temp->next) {
            // traverse adjacent vertexes.
            inDegree[node]--;
            if (inDegree[node] == 0) {
                zeroDegree.push(node);
            }
        }
    }
    if (cnt != graph.nodes.size())
    {
        // throw error
        throw "Graph is not a directed cyclical graph!";
        list<Node*> empty;
        return empty;
    }
    return ret;

}

全部代码：

#include<iostream>
#include<list>
#include<queue>
#include<stack>
#include<unordered_map>
#include<unordered_set>
using namespace std;
//解依赖
class Edge;
class Node {
public:
    int value;
    int in;
    int out;
    list<Node*> next;
    list<Edge*> edges;
    Node(int value) {
        this->value = value;
        in = 0;
        out = 0;
    }
};
class Edge {
public:
    int weight;
    Node* from;
    Node* to;

    Edge(int weight, Node* from, Node* to) {
        this->weight = weight;
        this->from = from;
        this->to = to;
    }
};
class Graph {
public:
    unordered_map<int, Node*> nodes;
    unordered_set<Edge*> edges;

};
class GraphGenerator {
public:
    Graph createGraph(int matrix[][3], int rows, int col) {
        Graph graph;
        for (int i = 0; i < rows; i++) {
            int weight = matrix[i][0];
            int from = matrix[i][1];
            int to = matrix[i][2];
            if (graph.nodes.find(from) == graph.nodes.end()) {
                graph.nodes[from] = new Node(from);
            }
            if (graph.nodes.find(to) == graph.nodes.end()) {
                graph.nodes[to] = new Node(to);
            }
            //以上两个if操作后，必能找到 from 好人to节点
            Node* fromNode = graph.nodes.find(from)->second;
            Node* toNode = graph.nodes.find(to)->second;
            //为 graph 和 from所在的node 准备 一条边
            Edge* newEdge = new Edge(weight, fromNode, toNode);
            //对于新增的一条边， 被指向节点的入度+1
            toNode->in++;
            //对于新增的一条边， 指向节点的出度+1，所指向的节点确定，指向该节点的边确定
            fromNode->out++;
            fromNode->next.push_back(toNode);
            fromNode->edges.push_back(newEdge);
            //两个if会保证建立节点，这里保证 边的存在。
            graph.edges.insert(newEdge);

        }
        return graph;
    }
};


list<Node*> sortedTopology(Graph& graph) {
    queue<Node*> zeroDegree;  // queue contains nodes that in degree is zero 
    unordered_map<Node*, int> inDegree;  // container collects in degree of all the node in graph
    unordered_map<int, Node*>::iterator ite = graph.nodes.begin(); // iterator for while loop
    list<Node*> ret; // return value
    int cnt = 0; // count if all the nodes are traversed.
    while (ite!=graph.nodes.end()) {
        // traverse all the node find out which node has zero in degree and push it into queue.

        inDegree[ite->second] = ite->second->in;
        if (ite->second->in == 0) {
            zeroDegree.push(ite->second);
        }
        ite++;
        
    }

    while (!zeroDegree.empty()) {
        Node* temp=zeroDegree.front();
        zeroDegree.pop();
        cnt++;
        ret.push_back(temp);
        // pop one
        for (auto node : temp->next) {
            // traverse adjacent vertexes.
            inDegree[node]--;
            if (inDegree[node] == 0) {
                zeroDegree.push(node);
            }
        }
    }
    if (cnt != graph.nodes.size())
    {
        // throw error
        throw "Graph is not a directed cyclical graph!";
        list<Node*> empty;
        return empty;
    }
    return ret;

}



int main() {
    GraphGenerator g;
    // int matrix[][3]= {{1,1,2},{2,2,3},{3,3,1}};
    int matrix[][3] = { {0,1,2},{0,1,3},{0,1,4},{0,2,3},{0,2,7},{0,7,3},
                {0,3,5},{0,4,6} };
    int length = sizeof(matrix) / sizeof(matrix[0]);
    Graph graph = g.createGraph(matrix, length, 3);
    Node* node = graph.nodes.find(1)->second;
    list<Node*> list = sortedTopology(graph);
    std::list<Node*>::iterator ite = list.begin();
    while (ite != list.end()) {
        cout << (*ite)->value << endl;
        ite++;
    }
    return 0;
}