LeetCode-63-不同路径II

问题

思路

**1. **我们用 f(i, j)来表示从坐标 (0, 0) 到坐标 (i,j) 的路径总数，u(i,j) 表示坐标 (i,j) 是否可行，如果坐标 (i,j) 有障碍物，u(i,j)=0，u(i,j)=1。

**2. ** 状态转移方程：

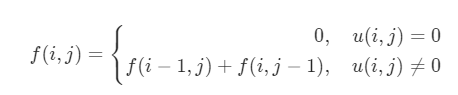
时间复杂度：O(nm)，其中 nn 为网格的行数，m 为网格的列数。我们只需要遍历所有网格一次即可。
空间复杂度：O(m)。利用滚动数组优化，我们可以只用 O(m) 大小的空间来记录当前行的 f值

代码

public static int uniquePathsWithObstacles(int[][] obstacleGrid) {
    int m = obstacleGrid.length, n = obstacleGrid[0].length;
    System.out.println(m);
    System.out.println(n);
    int[][] dp = new int[m][n];

    dp[0][0] = 1 - obstacleGrid[0][0];
    for (int i = 1; i < n; i++) {
        if (obstacleGrid[0][i] == 0 && dp[0][i - 1] == 1) {
            dp[0][i] = 1;
        }
    }
    for (int i = 1; i < m; i++) {
        if (obstacleGrid[i][0] == 0 && dp[i - 1][0] == 1) {
            dp[i][0] = 1;
        }
    }
    for (int i = 1; i < m; i++) {
        for (int j = 1; j < n; j++) {
            if (obstacleGrid[i][j] == 1) continue;
            dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
        }
    }
    return dp[m - 1][n - 1];