数学基础(二)
原文链接:http://www.one2know.cn/shuxuejichu2/
- 特征值的性质
![]()
- 奇异矩阵,不可逆矩阵,降秩矩阵
- 正交矩阵:n阶方阵A与其转置的乘积=E
- 线性无关组➡规范正交组
![]()
古典概型
- 排列数
![]()
- 组合数
![]()
- a为发生的事件.b为不发生的事件,概率
P=a/(a+b) - 联合概率:AB都发生的概率
P(AB)=P(A∩B),A和B事件独立时:P(AB)=P(A)P(B) - 条件概率:A在B已经发生条件下的发生概率
P(A|B)=P(AB)/P(B),例题2:
![]()
- 条件概率推广
![]()
- 全概率公式: 样本空间Ω=A1∪A2...∪An
![]()
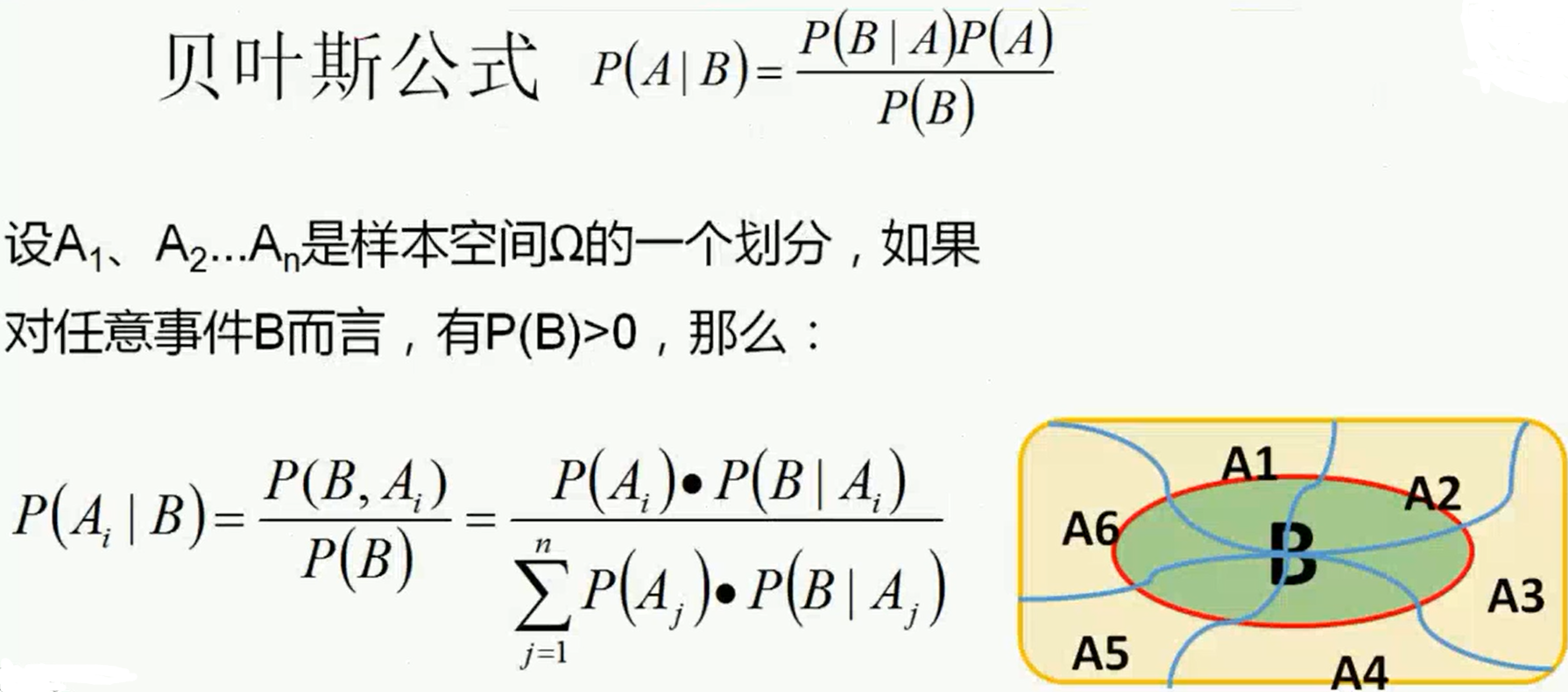
- 贝叶斯公式案例
![]()
![]()
离散变量分布
- Bernoulli(贝努利)分布,0-1分布,二点分布,
p与1-p,二项分布的特例 - 二项分布,多次Bernoulli实验,n次实验中出现k次的概率:
![]()
- Poisson(泊松)分布,λ>0是常数,泊松分布的期望和方差均为λ
![]()
![]()
- 二项分布与泊松分布的关系,n足够大时,
λ=np
二项分布数太大时不好计算,可用此方法转为泊松分布计算
![]()
连续变量分布
- 概率密度
f(x)的性质:
![]()
- 常用连续随机变量
1)均匀分布
![]()
2)指数分布
![]()
3)正态分布,μ是期望,σ是标准差.μ=0,σ=1是标准正态分布
![]()
4)Γ-分布:
Γ-函数:![]()
数字特征
- 期望
![]()
![]()
- 方差:衡量数据偏移程度
![]()
连续型:![]()
离散型:![]()
- 方差与期望的关系
![]()
- 标准差
![]()
- 协方差:衡量两个变量的总体误差,两个变量独立,则协方差为0
![]()
![]()
中心矩 峰度 最大似然
- 中心矩,原点矩
![]()
- 峰度,峰度>3,峰的形状尖,比正态分布要陡,反之亦然
![]()
- 偏度系数,描述分布对称性,系数为0,分布对称,>0右偏,<0左偏
![]()
- 切比雪夫定理
![]()
- 大数定律
![]()
- 中心极限定理
![]()
- 点估计,矩估计
![]()
![]()
- 极大似然估计,实际情况除概率估计总量,求解步骤:
![]()


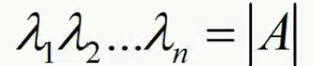

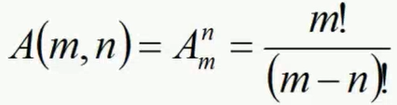
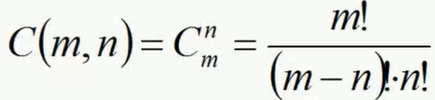

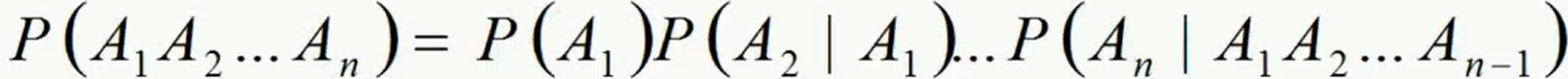


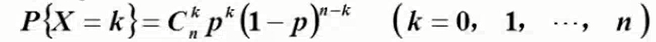


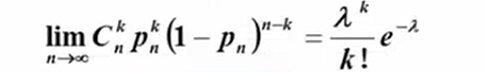
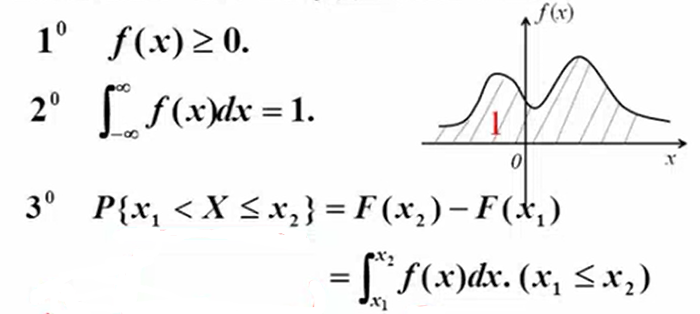
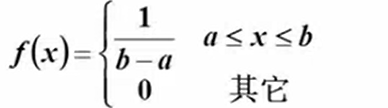
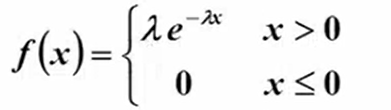
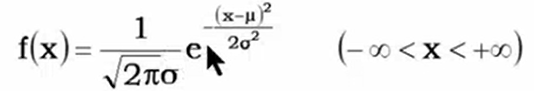
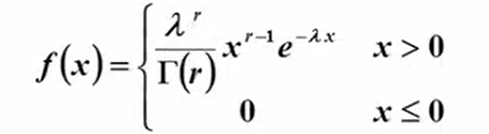
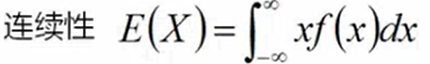
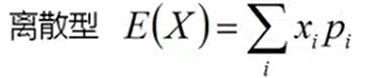
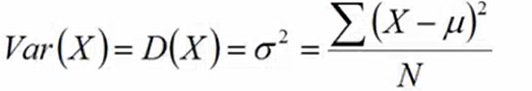
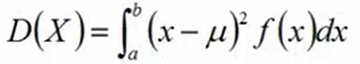
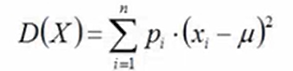
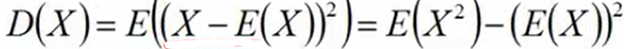
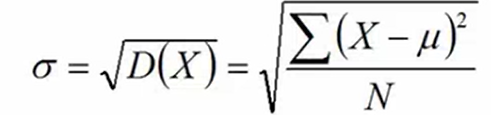
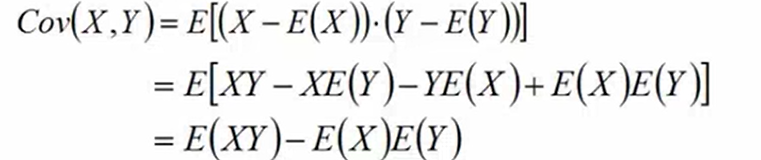


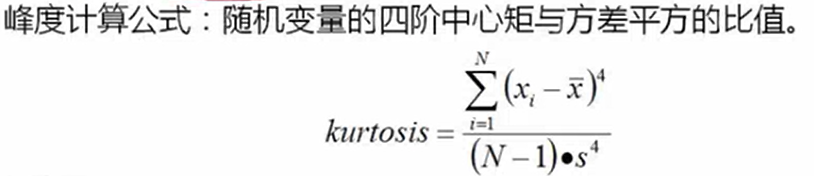
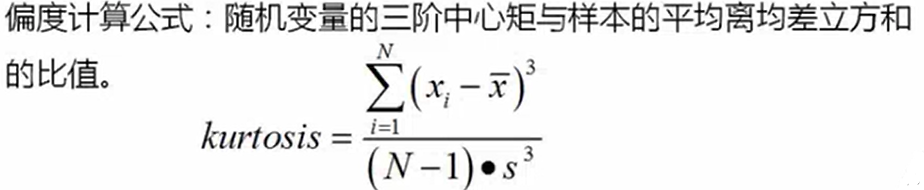



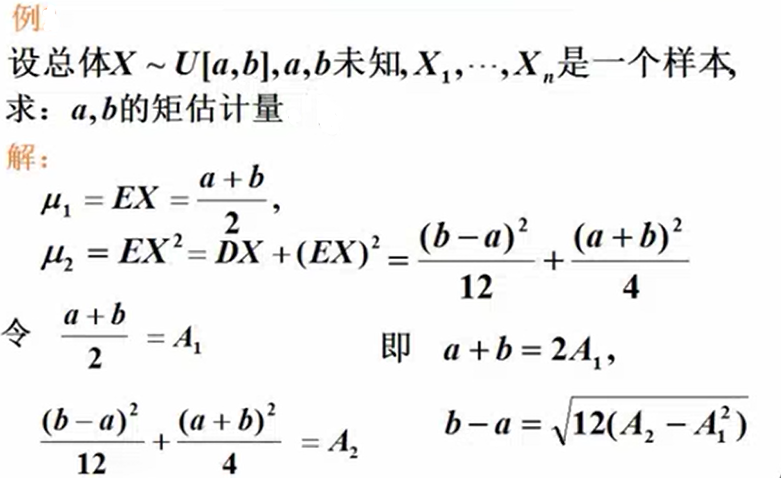
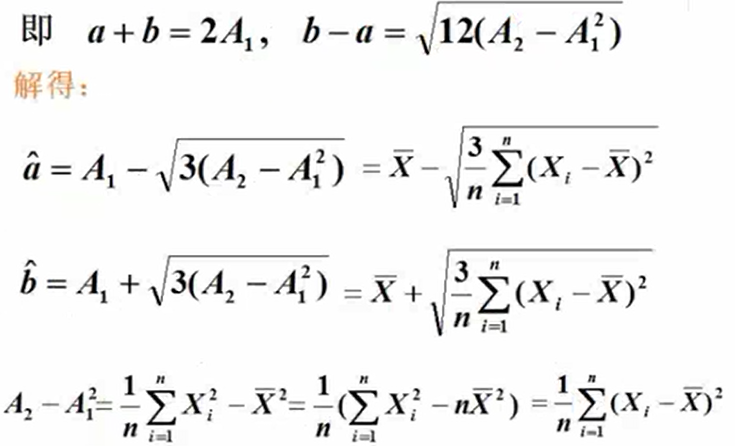


 浙公网安备 33010602011771号
浙公网安备 33010602011771号