Houdini MPM 笔记

// 变形梯度（Deformation Gradient)

 变形梯度 F 是连续介质力学中描述物体局部变形的核心张量，它完整刻画了材料点附近无限小区域的变形（拉伸/剪切）和刚性旋转。 其数学定义为：

 直观理解：

变形梯度 F 将一个参考构型中的微小线段 dX 映射到当前构型中的线段 dx=F⋅ dX，同时包含了该点的局部旋转和形变信息。

 

变形梯度的关键特性：

 // 变形梯度在物理仿真中的应用

 // 体积变化率 J = det(F) = Jp * Je

J = det(F)的物理意义，即体积变化率。然后分解成Jp和Je，说明弹性部分Je对应可恢复的体积变化，而塑性部分Jp对应不可逆的体积变化。例如，金属塑性变形通常假设体积不变，所以Jp=1，而Je可能包含弹性体积变化。但对于多孔材料，Jp可能不等于1，这时候就需要考虑塑性体积变化。

 // 从MPM结算的粒子中筛选POP发射源

这是官方MasterClass的一个案例。艺术家先是用MPM结算了主体的Snow , 然后想在这些Snow的主体粒子中帅选出粒子作为POP发射源。比较有意思的是在vex中通过比较ΔJp，ΔJp>0说明塑性体积在膨胀变大，可以筛选出这部分做发射源，增加细节。

 

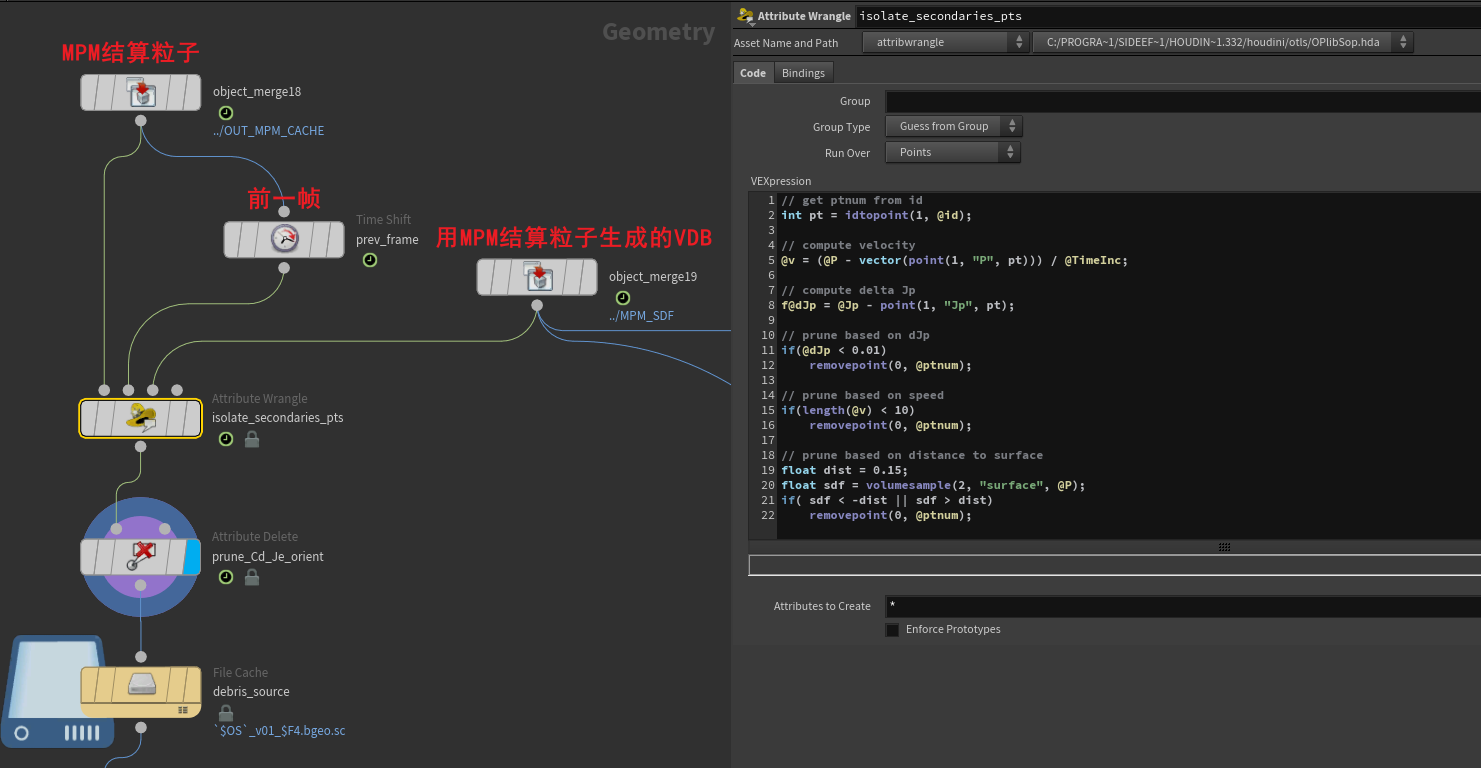
// get ptnum from id
int pt = idtopoint(1, @id);

// compute velocity
@v = (@P - vector(point(1, "P", pt))) / @TimeInc;

// compute delta Jp
f@dJp = @Jp - point(1, "Jp", pt);

// prune based on dJp
if(@dJp < 0.01)
    removepoint(0, @ptnum);

// prune based on speed    
if(length(@v) < 10)
    removepoint(0, @ptnum);

// prune based on distance to surface
float dist = 0.15;
float sdf = volumesample(2, "surface", @P);
if( sdf < -dist || sdf > dist)
    removepoint(0, @ptnum);

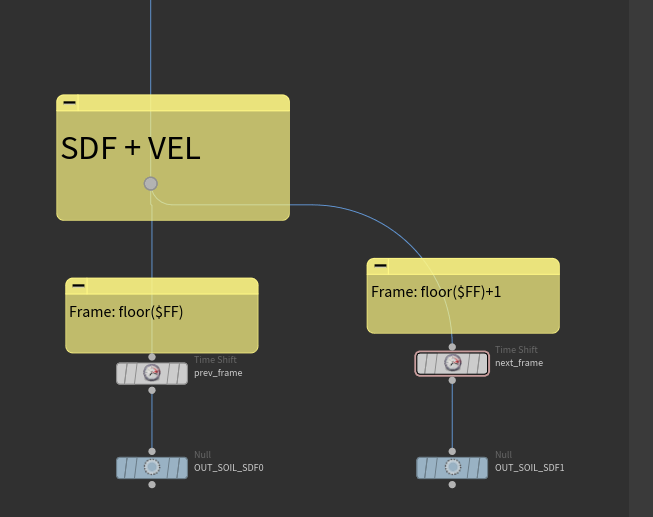
 // Fast SDF Collision

输入端口1是碰撞SDF + VEL 场

float sdf;
vector grad, vel;
    
sdf = volumesample(1, 0, @P) - @pscale;
       
if (sdf < 0)
{
    grad = normalize(volumegradient(1, 0, @P));
    vel = volumesamplev(1, "vel", @P);
    
    @P -= grad * sdf;

    vector rel_vel = @v - vel;
    float friction = 1;
    float sticky = 0;

    float v_dot_n = dot(rel_vel, grad);
    if (v_dot_n < sticky)
    {
        vector v_tangent = rel_vel - grad * v_dot_n;
        v_dot_n = abs(v_dot_n);
        float v_tangent_length = length(v_tangent);
        if (v_tangent_length <= friction * v_dot_n)
        {
            // static friction
            rel_vel = 0;
        }
        else
        {
            // dynamic friction
            rel_vel = v_tangent - (friction * v_dot_n * v_tangent) / v_tangent_length;
        }
    
            @v = rel_vel + vel;
    }
}

  // 做粒子结算时，如果substep>1, 这时如果想要准确点的SDF, 可以这样简单的插值

float bias = frac(@Frame);
    
vector vel0 = volumesamplev(0, "vel", @P);
vector vel1 = volumesamplev(1, "vel", @P);
vel = lerp(vel0, vel1, bias);

// compute sample pos
vector pos0 = @P - bias * @TimeInc * vel;
vector pos1 = @P + (1.0f - bias) * @TimeInc * vel;

// sample sdf
float sdf0 = volumesample(0, "surface", pos0);
float sdf1 = volumesample(1, "surface", pos1);

sdf = lerp(sdf0, sdf1, bias) - @pscale;

输入端口0，1，如下

 // 计算平均orient

输入是一些点，每个点都有自己的orient属性。想计算这些点的平均orient可以这样操作。

先把所有点的orient属性写入到detail的数组里面

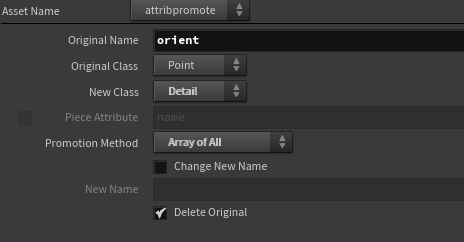
 然后转移到点上

p[]@orients = detail(1, "orient");

最后

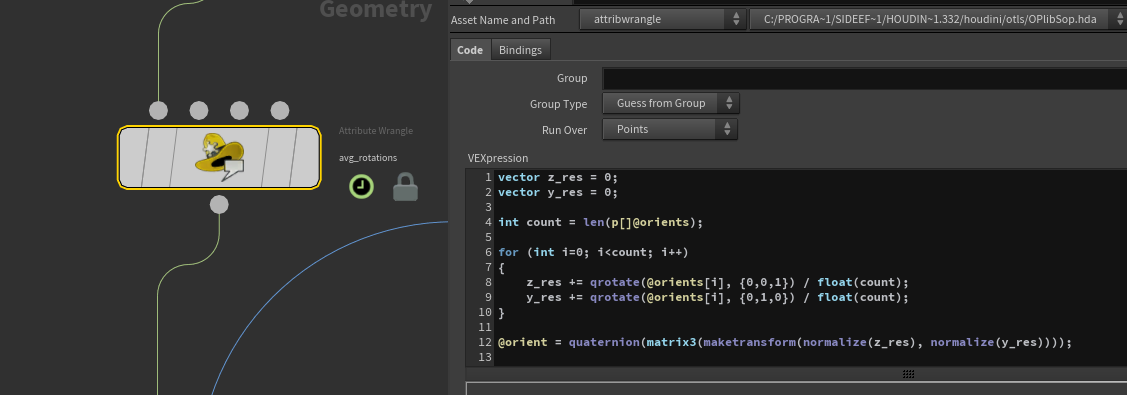
vector z_res = 0;
vector y_res = 0;

int count = len(p[]@orients);

for (int i=0; i<count; i++)
{
    z_res += qrotate(@orients[i], {0,0,1}) / float(count);
    y_res += qrotate(@orients[i], {0,1,0}) / float(count);
}

@orient = quaternion(matrix3(maketransform(normalize(z_res), normalize(y_res))));