Matplotlib库的介绍
Matplotlib库的介绍

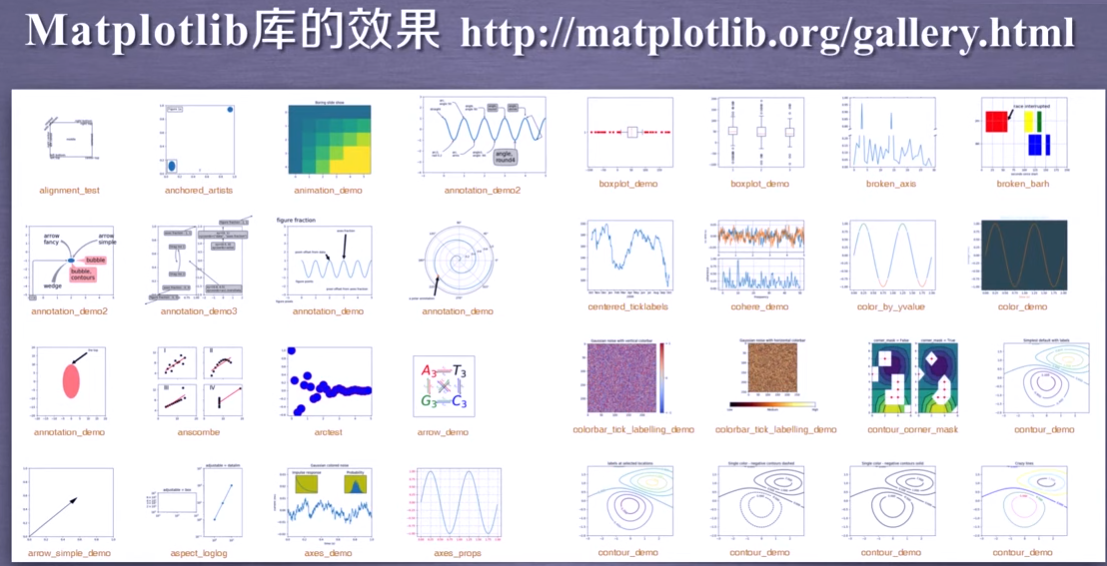
Matplotlib库由各种可视化类构成,内部结构复杂,受Matlab启发。
Matplotlib.pyplot是绘制各类可视化图形的命令子库,相当于快捷方式。
import matplotlib.pyplot as plt
Matplotlib库实例:
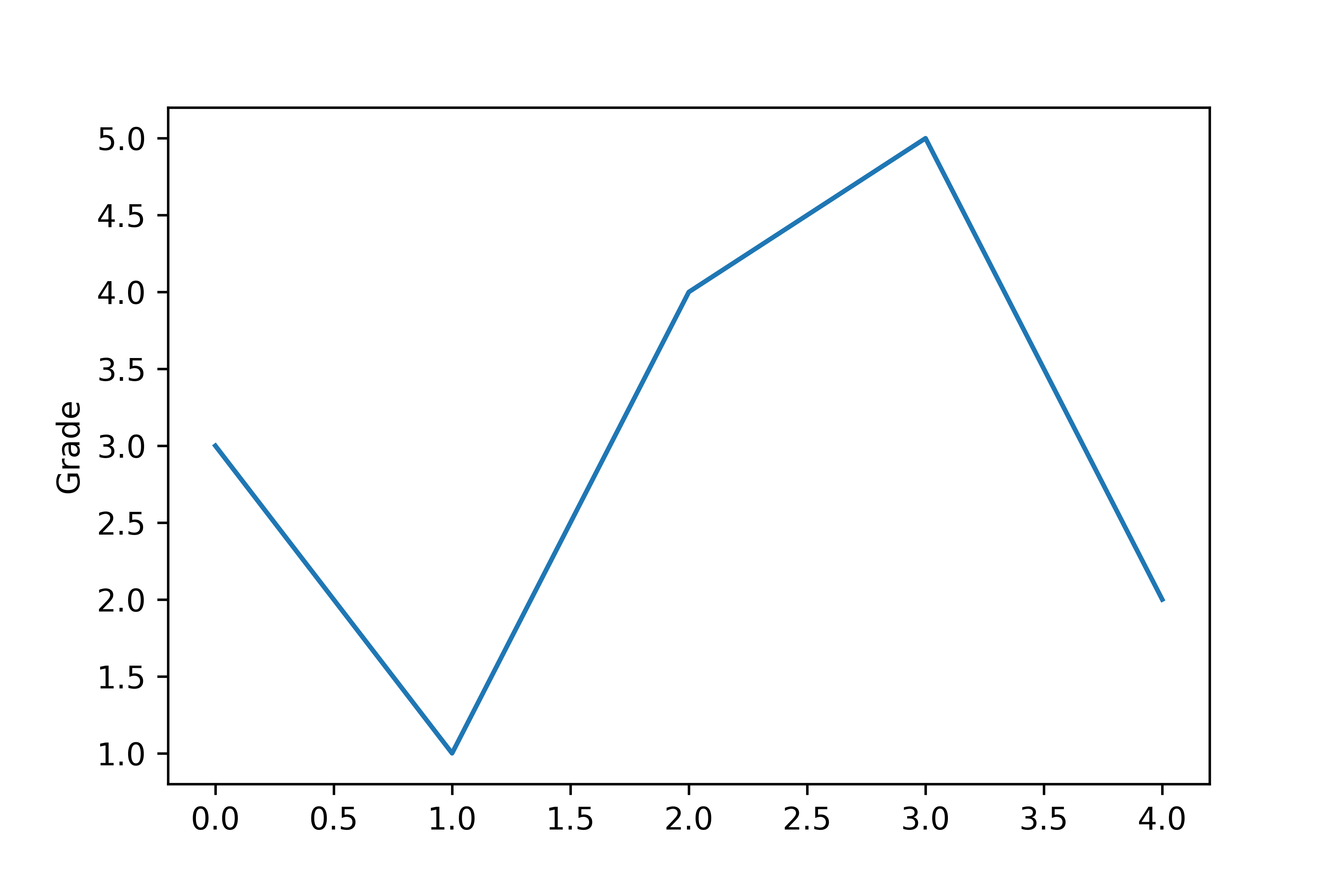
1、绘制Y轴图形并保存png文件
import matplotlib.pyplot as plt
#当只有一个输入列表参数时,这个参数会被当做Y轴来处理
#X轴默认是这个列表的索引即[0, 1, 2, 3, 4],X轴自动生成,横坐标值0-4之间
plt.plot([3, 1, 4, 5, 2])
plt.ylabel("Grade")
#将输出图形存储为文件,默认PNG格式,可以通过dpi(每英寸空间包含的点的数量)修改输出质量
plt.savefig("matplotlib_example_1", dpi=600) #保存为PNG文件
plt.show()
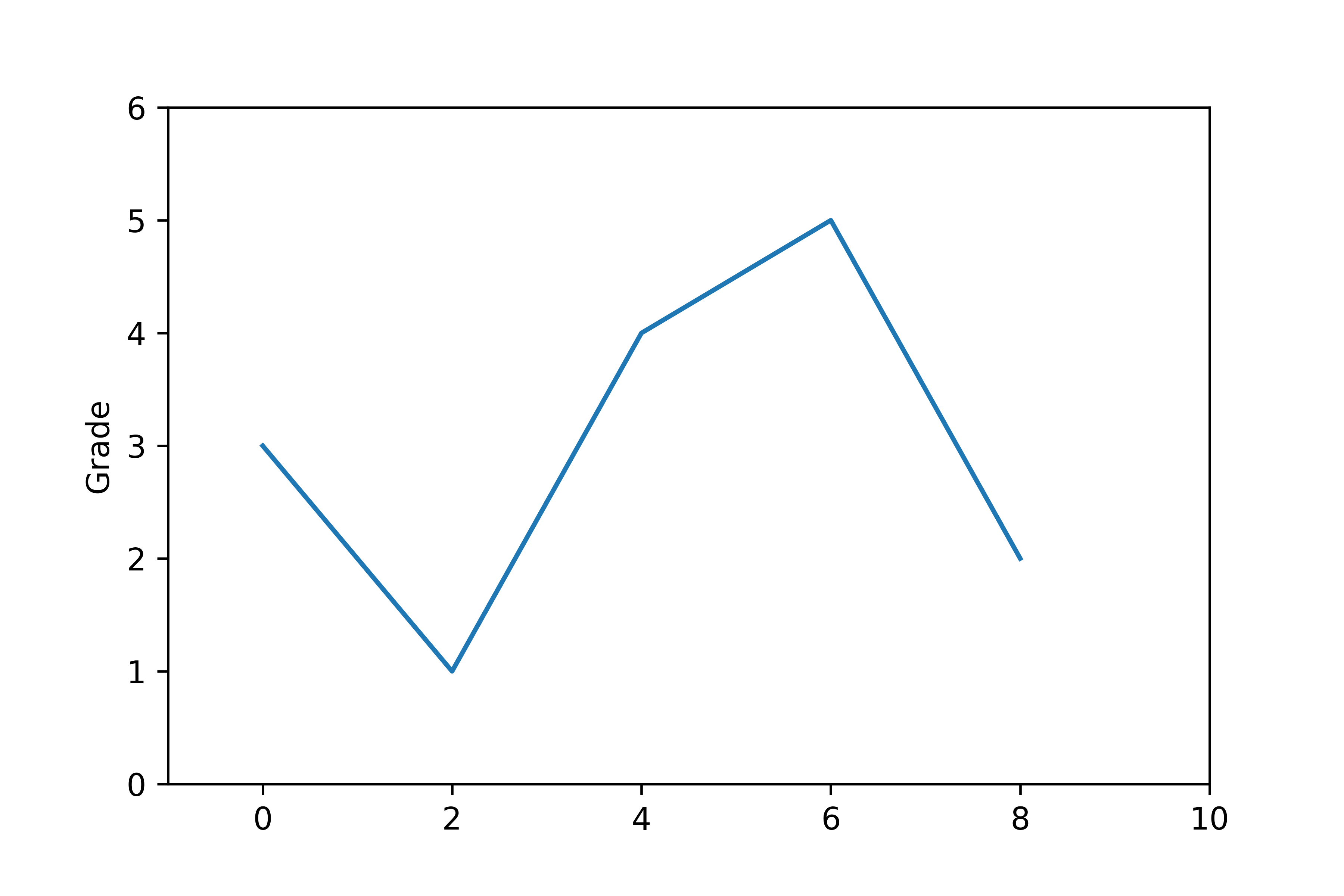
2、同时控制X,Y轴点的绘制
import matplotlib.pyplot as plt
# plt.plot(x,y)当有两个以上参数时,按照X轴和Y轴顺序绘制数据点。
plt.plot([0, 2, 4, 6, 8], [3, 1, 4, 5, 2])
plt.ylabel("Grade")
#设定横纵坐标尺度,[-1,10]表示X轴的坐标起始于-1,终止于10;
#[0,6]表示Y轴的坐标起始于0,终止于6
plt.axis([-1, 10, 0, 6])
plt.show()
3、pyplot的绘图区域
plt.subplot(nrows, ncols, plot_number)
#将绘图区域分割成了以nrows横轴数量,以ncols纵轴数量的绘图区域
#plot_number指定当前绘图区在哪个区域
#3个横轴,两个纵轴,共6个区域,当前为第4个区域
plt.subplot(3, 2, 4)
plt.subplot(324) # 可以把中间的逗号去掉
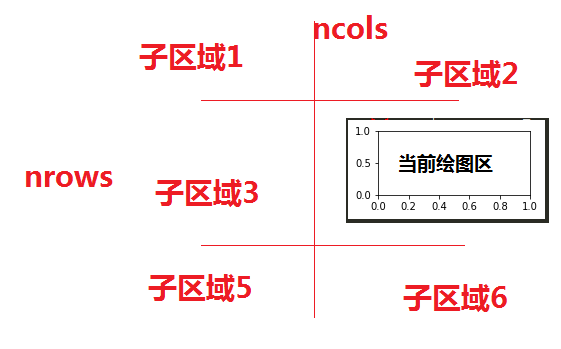
在全局绘图区域创建一个分区体系,并通过plot_number能够定位到当前绘图的子绘图区域。
示例:
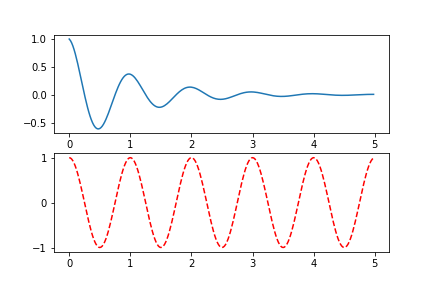
import numpy as np
import matplotlib.pyplot as plt
def f(t):
return np.exp(-t) * np.cos(2*np.pi*t)
a = np.arange(0.0, 5.0, 0.02)
plt.subplot(211)
plt.plot(a, f(a))
plt.subplot(2, 1, 2)
plt.plot(a, np.cos(2*np.pi*a), 'r--')
plt.show()
4、pyplot的plot()函数
plt.plot(x, y, format_string, **kwargs)
x:X轴数据,列表或数组,可选。
y:Y轴数据,列表或数组。
format_string:控制曲线的格式字符串,可选。
由颜色字符、风格字符和标记字符组成,它们可以组合使用。
颜色字符是控制曲线的色彩的方法
颜色字符 说明 颜色字符 说明
'b' 蓝色 'm' 洋红色magenta
'g' 绿色 'y' 黄色
'r' 红色 'k' 黑色
'c' 青绿色cyan 'w' 白色
'#008000' RGB某颜色 '0.8' 灰度值字符串
风格字符表示的是曲线的样子
风格字符 说明
'-' 实线
'--' 破折线
'-.' 点划线
':' 虚线
'' ' '(空或者空格) 无线条
标记字符指的是在曲线中的每一个数据点采用什么方式标明出来
标记字符 说明 标记字符 说明 标记字符 说明
'.' 点标记 '1' 下花三角标记 'h' 竖六边形标记
',' 像素标记(极小点) '2' 上花三角标记 'H' 横六边形标记
'o' 实心圈标记 '3' 左花三角标记 '+' 十字标记
'v' 倒三角标记 '4' 右花三角标记 'x' x标记
'^' 上三角标记 's' 实心方形标记 'D' 菱形标记
'>' 右三角标记 'p' 实心五角标记 'd' 瘦菱形标记
'<' 左三角标记 '*' 星形标记 '|' 垂直线标记
**kwargs:第二组或更多(x, y, format_string)。
color:控制颜色,color='green'
linestyle:线条风格,linestype='dashed'
marker:标记风格。marker='o'
markerfacecolor:标记颜色,markerfacecolor='blue'
markersize:标记尺寸,markersize=20
......
当绘制多条曲线时,各条曲线的x不能省略。
如果只绘制一条曲线,我们可以把x轴的数据省略,只给y轴数据,
y轴数据的索引值可以作为x轴数据自动绘制出来。
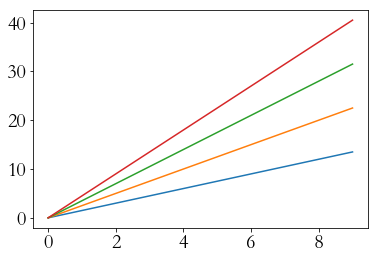
import matplotlib.pyplot as plt
import numpy as np
a = np.arange(10)
plt.plot(a, a*1.5, a, a*2.5, a, a*3.5, a, a*4.5)
plt.show()
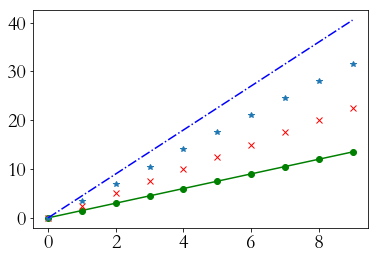
plt.plot(a, a*1.5, 'go-', a, a*2.5, 'rx', a, a*3.5, '*', a, a*4.5, 'b-.')
plt.show()
5、pyplot的中文显示
第一种方法:
pyplot并不默认支持中文显示,需要rcParams修改字体实现。
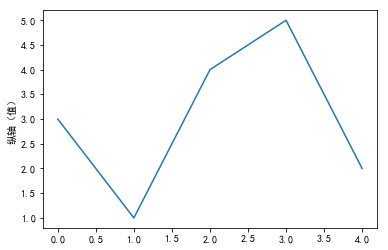
import matplotlib.pyplot as plt
import matplotlib
matplotlib.rcParams['font.family']='SimHei'
plt.plot([3, 1, 4, 5, 2])
plt.ylabel("纵轴(值)")
plt.show()
rcParams的属性
属性 说明
'font.family' 用于显示字体的名字
'font.style' 字体风格,正常'normal'或斜体'italic'
'font.size' 字体大小,整数字号或者'large'、'x-small'
中文字体 说明
'SimHei' 中文黑体
'Kaiti' 中文楷体
'LiSu' 中文隶书
rcParams['font.family'] 'FangSong' 中文仿宋
'YouYuan' 中文幼圆
'STSong' 华文宋体
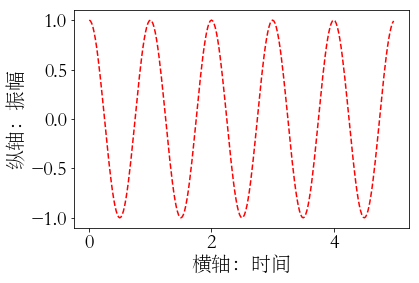
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
matplotlib.rcParams['font.family']='STSong'
matplotlib.rcParams['font.size']=20
a=np.arange(0.0, 5.0, 0.02)
plt.xlabel('横轴:时间')
plt.ylabel('纵轴:振幅')
plt.plot(a, np.cos(2*np.pi*a),'r--')
plt.show()
第二种方法:
在有中文输出的地方,增加一个属性:fontproperties
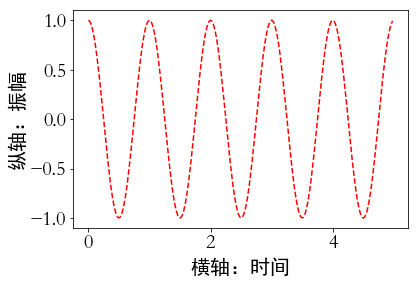
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
a=np.arange(0.0, 5.0, 0.02)
plt.xlabel('横轴:时间', fontproperties='SimHei', fontsize=20)
plt.ylabel('纵轴:振幅', fontproperties='SimHei', fontsize=20)
plt.plot(a, np.cos(2*np.pi*a),'r--')
plt.show()
6、pyplot的文本显示
pyplot的文本显示函数
函数 说明
plt.xlabel() 对X轴增加文本标签
plt.ylabel() 对Y轴增加文本标签
plt.title() 对图形整体增加文本标签
plt.text() 在任意位置增加文本
plt.annotate() 在图形中增加带箭头的注解
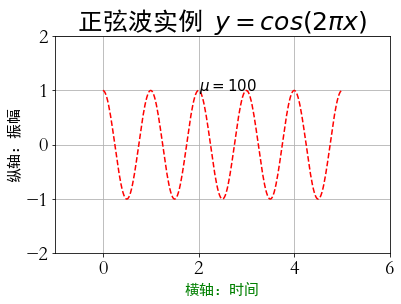
import numpy as np
import matplotlib.pyplot as plt
a=np.arange(0.0, 5.0, 0.02)
plt.plot(a, np.cos(2*np.pi*a),'r--')
plt.xlabel('横轴:时间', fontproperties='SimHei', fontsize=15, color='green')
plt.ylabel('纵轴:振幅', fontproperties='SimHei', fontsize=15)
plt.title(r'正弦波实例 $y=cos(2\pi x)$', fontproperties='SimHei', fontsize=25)
plt.text(2, 1, r'$\mu=100$', fontsize=15) # $ $中间的文本是Latex文本
plt.axis([-1, 6, -2, 2])
plt.grid(True)
plt.show()
plt.annotate(s, xy=arrow_crd, xytext=text_crd, arrowprops=dict)
s:表示要注解的字符串内容
xy:箭头所在的位置
xytext:文本显示的位置
arrowprops:箭头显示的属性
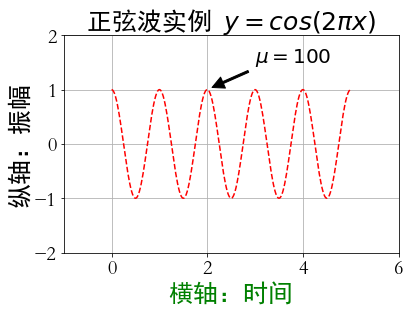
import numpy as np
import matplotlib.pyplot as plt
a=np.arange(0.0, 5.0, 0.02)
plt.plot(a, np.cos(2*np.pi*a),'r--')
plt.xlabel('横轴:时间', fontproperties='SimHei', fontsize=25, color='green')
plt.ylabel('纵轴:振幅', fontproperties='SimHei', fontsize=25)
plt.title(r'正弦波实例 $y=cos(2\pi x)$', fontproperties='SimHei', fontsize=25)
plt.annotate(r'$\mu=100$', xy=(2, 1), xytext=(3, 1.5),\
arrowprops=dict(facecolor='black', shrink=0.1, width=2))
plt.axis([-1, 6, -2, 2])
plt.grid(True)
plt.show()
7、pyplot的子绘图区域
复杂的绘图区域
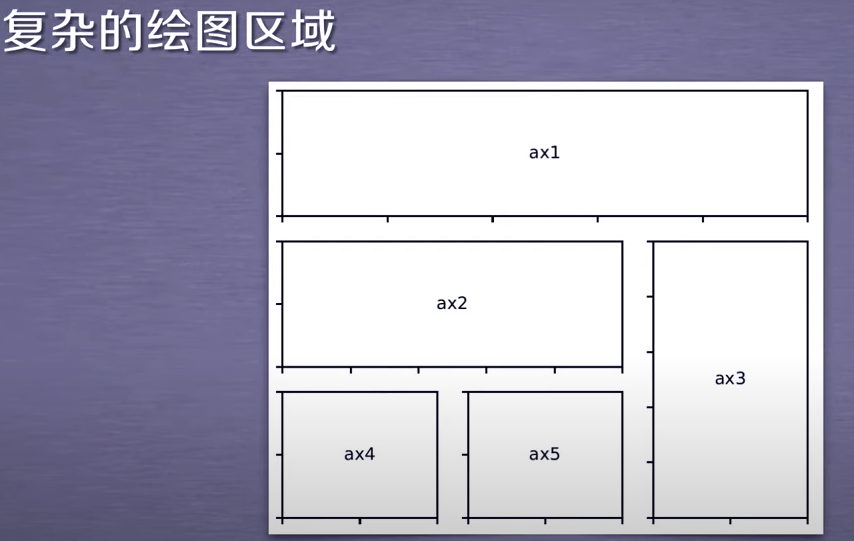
plt.subplot2grid()
plt.subplot2grid(GridSpec, CurSpec, colspan=1, rowspan=1)
理念:设定网格,选中网格,确定选中行列区域数量,编号从0开始。
选定第二行开始的ax2区域
plt.subplot2grid((3,3),(1,0),colspan=2)
(3,3)表示:将一个区域分割成3行3列9块区域
(1,0)表示:当前为subplot选定的位置在第1行第0列
colspan表示:列的延伸,从选定的(1,0)开始,在列的方向上延伸2个长度
plt.subplot2grid((3,3),(0,0),colspan=3)#ax1 ... |
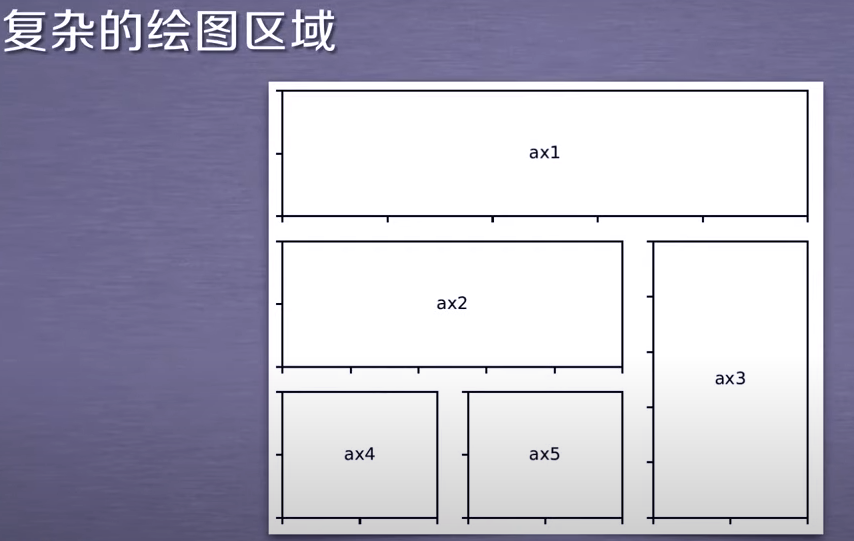 |
GridSpec类
import matplotlib.gridspec as gridspec
gs = gridspec.GridSpec(3,3)
ax1 = plt.subplot(gs[0, :])
ax2 = plt.subplot(gs[1, :-1])
ax3 = plt.subplot(gs[1:, -1])
ax4 = plt.subplot(gs[2, 0])
ax5 = plt.subplot(gs[2, 1])
通过使用GridSpec类配合subplot也可以对子区域进行划定和选择
Nested GridSpecs
This example demonstrates the use of nested GridSpecs.
import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec
import numpy as np
from itertools import product
def squiggle_xy(a, b, c, d):
i = np.arange(0.0, 2*np.pi, 0.05)
return np.sin(i*a)*np.cos(i*b), np.sin(i*c)*np.cos(i*d)
fig = plt.figure(figsize=(8, 8))
# gridspec inside gridspec
outer_grid = gridspec.GridSpec(4, 4, wspace=0.0, hspace=0.0)
for i in range(16):
inner_grid = gridspec.GridSpecFromSubplotSpec(3, 3,\
subplot_spec=outer_grid[i], wspace=0.0, hspace=0.0)
a = i // 4 + 1
b = i % 4 + 1
for j, (c, d) in enumerate(product(range(1, 4), repeat=2)):
ax = fig.add_subplot(inner_grid[j])
ax.plot(*squiggle_xy(a, b, c, d))
ax.set_xticks([])
ax.set_yticks([])
fig.add_subplot(ax)
all_axes = fig.get_axes()
# show only the outside spines
for ax in all_axes:
for sp in ax.spines.values():
sp.set_visible(False)
if ax.is_first_row():
ax.spines['top'].set_visible(True)
if ax.is_last_row():
ax.spines['bottom'].set_visible(True)
if ax.is_first_col():
ax.spines['left'].set_visible(True)
if ax.is_last_col():
ax.spines['right'].set_visible(True)
plt.show()

Matplotlib库有上百种图形绘制方法,我们不可能掌握每一种绘制方法。

理解数据对应的含义以及展示这种含义的图形显示方法,这种关联是非常重要的。当我们确定了数据显示风格的关联性,
找到了这组数据对应的最好的显示方法,我们可以看Matplotlib的文档,来找到它的实际的绘制方法并且绘制出来。
8、pyplot基础图表函数概述
16种常用的pyplot基础图表函数
函数 说明
plt.plot(x,y,fmt,...) 绘制一个坐标图
plt.boxplot(data,notch,position) 绘制一个箱形图
plt.bar(left,height,width,bottom) 绘制一个条形图
plt.barh(width,bottom,left,height) 绘制一个横向条形图
plt.polar(theta,r) 绘制极坐标图
plt.pie(data,explode) 绘制饼图
plt.psd(x,NFFT=256,pad_to,Fs) 绘制功率谱密度图
plt.specgram(x,NFFT=256,pad_to,F) 绘制图谱
plt.cohere(x,y,NFFT=256,Fs) 绘制X-Y的相关性函数
plt.scatter(x,y) 绘制散点图,其中,x和y长度相同
plt.step(x,y,where) 绘制步阶图
plt.hist(x,bins,normed) 绘制直方图
plt.contour(X,Y,Z,N) 绘制等值图
plt.vlines() 绘制垂直图
plt.stem(x,y,linefmt,markerfmt) 绘制柴火图
plt.plot_date() 绘制数据日期
pyplot饼图的绘制
import matplotlib.pyplot as plt
#给定每一块对应的标签
labels = 'Frogs', 'Hogs', 'Dogs', 'Logs'
#约定饼图各块的尺寸
sizes = [15, 30, 45, 10]
#指出哪块该突出出来
explode = (0, 0.1, 0, 0)
#autopct:表示中间显示百分数的方式
#shadow:表示饼图是一个二维饼图还是一个带有阴影的饼图效果
#startangle:表示饼图起始角度
plt.pie(sizes, explode=explode, labels = labels, autopct='%1.1f%%',
shadow=False, startangle=90)
plt.show()
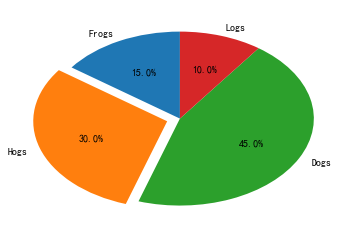
import matplotlib.pyplot as plt
labels = 'Frogs', 'Hogs', 'Dogs', 'Logs'
sizes = [15, 30, 45, 10]
explode = (0, 0.1, 0, 0)
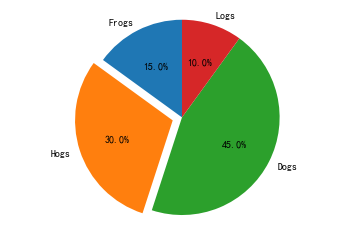
plt.pie(sizes, explode=explode, labels = labels, autopct='%1.1f%%',
shadow=False, startangle=90)
#在绘制图形时,其中的x、y方向尺寸应该是相等的
plt.axis('equal')
plt.show()
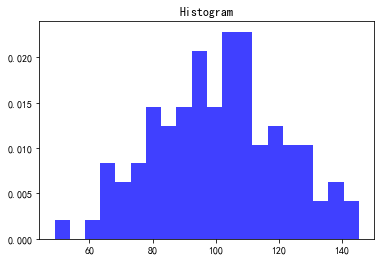
pyplot直方图的绘制
import numpy as np
import matplotlib.pyplot as plt
#设定一个随机种子
np.random.seed(0)
mu, sigma = 100, 20 #均值和标准差
#生成一个给定均值和方差,元素是正态分布特点的数组
a = np.random.normal(mu, sigma, size=100)
#绘制直方图,
#20是bin:表示直方图的个数,
#直方图的原理:对于一个数组a,它有若干个元素,有最小值和最大值,在这之间就构成了一个取值范围
#直方图的做法是,将取值范围,也就是数组a最小值和最大值之间,均等的划分bin个区间,划出相等区间之后
#数组中的元素就在这些直方图中分布,所以在数组最小值和最大值之间,通过直方图均分之后,
#每一个直方图中包含的数组元素个数就构成了直方图的高度
#normed=1表示将每一个直方中出现元素的个数归一化为出现的概率,所以纵坐标是一个小数比例
#normed=0表示纵坐标在这个直方区域中间出现的数组a的元素个数
#通过直方图可以很好的将一个数组,它在一个最小值到最大值取值范围内,将它的个数绘制出相关的图形
#有效的展示出来,直方图也能够规划,协调,看到数据在个数层面和取值方面的一种分布。
#histtype:直方图的绘制类型
#facecolor:直方图的颜色
#alpha:透明度
plt.hist(a, 20, normed=1, histtype='stepfilled', facecolor='b', alpha=0.75)
#显示标题信息
plt.title('Histogram')
plt.show()
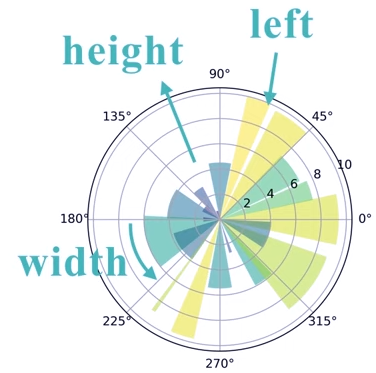
pyplot极坐标图的绘制
面向对象绘制极坐标:
import numpy as np
import matplotlib.pyplot as plt
#表示绘制极坐标图中数据的个数
N = 20
#从0到360度,按照个数等分出N个不同的角度
theta = np.linspace(0.0, 2* np.pi, N, endpoint=False)
#生成每个角度对应的值
radii = 10 * np.random.rand(N)
#给出宽度值
width = np.pi / 4 * np.random.rand(N)
#projection='polar':绘制极坐标的指示
#将这样一个子绘图区域形成一个对象ax
ax = plt.subplot(111, projection = 'polar')
#ax.bar绘制极坐标
#theta:left,指的是绘制极坐标系中那些颜色区域的时候从哪开始的,
# 表示的是图中的某一个位置
#radii:height,从中心点向边缘绘制的长度
#width:width,每一个绘图区域的面积,角度范围内辐射的面积
bars = ax.bar(theta, radii, width = width, bottom = 0.0)
for r, bar in zip(radii, bars):
#每一个绘制极坐标区域的颜色进行设定
bar.set_facecolor(plt.cm.viridis(r / 10.))
bar.set_alpha(0.5)
plt.show()
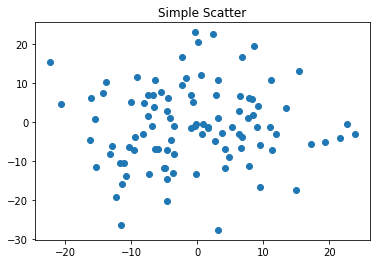
pyplot散点图的绘制
什么是散点图?
在坐标系中,每一个值用一个点来表示的图。
import numpy as np
import matplotlib.pyplot as plt
#生成一个对象
#分别对应图表(fig)以及图表相关的区域(ax)
#默认绘制区域111
fig, ax = plt.subplots()
#绘制'o'型标点的点
ax.plot(10 * np.random.randn(100), 10 * np.random.randn(100), 'o')
ax.set_title('Simple Scatter')
plt.show()
“引力波的绘制”实例介绍
引力波
物理学中,引力波是因为时空弯曲对外以辐射形式传播的能量。
爱因斯坦基于广义相对论预言了引力波的存在
2016年6月16日,LIGO合作组宣布2015年12月26日03:38:53(UTC),
两台不同位置的引力波探测器同时探测到了一个引力波信号。
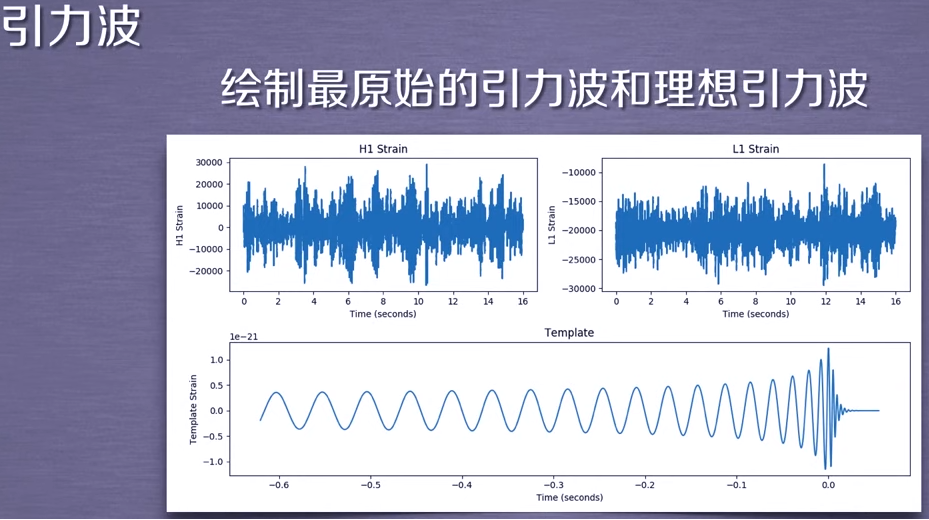
引力波绘制代码解读:
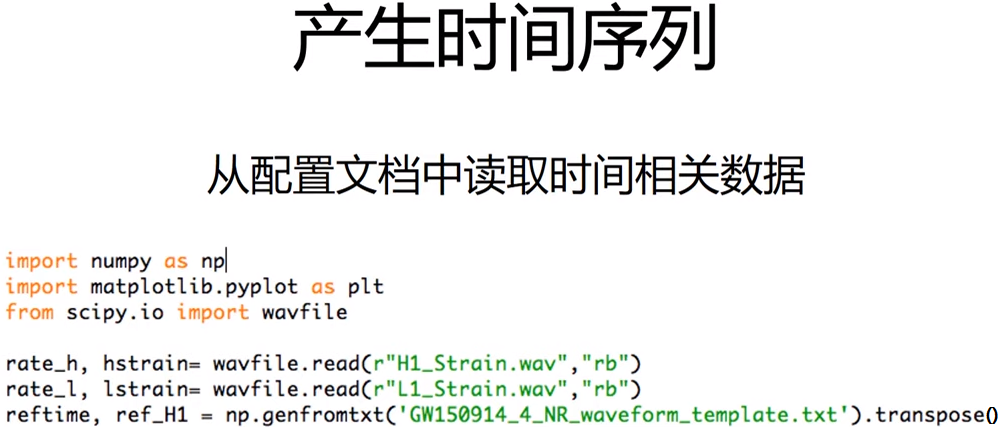
1、产生时间序列
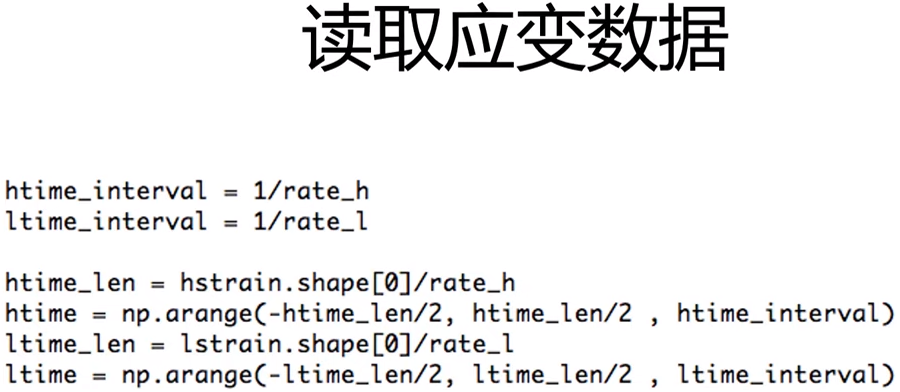
2、读取应变数据
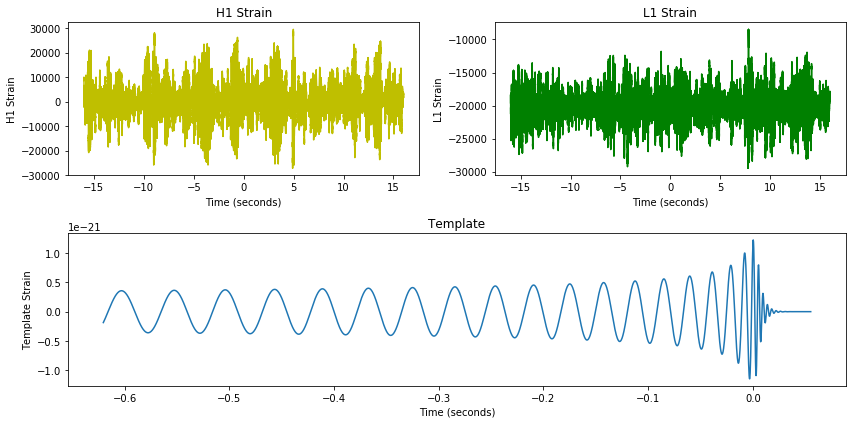
3、绘制H1 Strain

4、绘制L1 Strain & Template

5、显示并保存图像

“引力波的绘制”代码
H1_Strain.wav
L1_Strain.wav
GW150914_4_NR_waveform_template.txt
import numpy as np
import matplotlib.pyplot as plt
from scipy.io import wavfile
rate_h, hstrain = wavfile.read(r"H1_Strain.wav", "rb")
rate_l, lstrain = wavfile.read(r"L1_Strain.wav", "rb")
reftime, ref_H1 = np.genfromtxt('GW150914_4_NR_waveform_template.txt').transpose()
htime_interval = 1/rate_h
ltime_interval = 1/rate_l
htime_len = hstrain.shape[0]/rate_h
htime = np.arange(-htime_len / 2, htime_len / 2, htime_interval)
ltime_len = lstrain.shape[0]/rate_l
ltime = np.arange(-ltime_len / 2, ltime_len / 2, ltime_interval)
fig = plt.figure(figsize=(12, 6))
plth = fig.add_subplot(221)
plth.plot(htime, hstrain, 'y')
plth.set_xlabel('Time (seconds)')
plth.set_ylabel('H1 Strain')
plth.set_title('H1 Strain')
pltl = fig.add_subplot(222)
pltl.plot(ltime, lstrain, 'g')
pltl.set_xlabel('Time (seconds)')
pltl.set_ylabel('L1 Strain')
pltl.set_title('L1 Strain')
pltref = fig.add_subplot(212)
pltref.plot(reftime, ref_H1)
pltref.set_xlabel('Time (seconds)')
pltref.set_ylabel('Template Strain')
pltref.set_title('Template')
fig.tight_layout()
plt.savefig("Gravitational_Waves_Original.png")
plt.show()
plt.close(fig)
posted on 2020-06-26 20:21 pencil2001 阅读(1279) 评论(0) 收藏 举报


 浙公网安备 33010602011771号
浙公网安备 33010602011771号