P6018 [Ynoi2010] Fusion tree 题解

题目描述

给定 \(n\) 个点的树，点有点权 \(a_i\) 。

接下来 \(m\) 次操作：

• 1 x ：将所有与 \(x\) 相邻的节点权值 \(+1\) 。
• 2 x v ：将节点 \(x\) 的权值减去 \(v\) 。
• 3 x ：询问所有与 \(x\) 相邻的节点的权值异或和。

数据范围

• \(1\le n,m\le 5\cdot 10^5,0\le a_i\le 10^5,1\le x\le n\) 。

保证任意时刻所有节点权值非负。

时间限制 \(\texttt{2s}\) ，空间限制 \(\texttt{500MB}\) 。

分析

先考虑一个究极弱化版问题：邻点权值 \(+1\) ，单点查询。

解决方法也很经典：任意钦定一个点为根，维护加法标记，表示给所有子节点要增加的权值，修改时打标记并单独更新父节点，查询结果为自身权值加上父节点的标记。

因此对于本题，操作二只需先单点查询，再将更新后的权值插入父节点的数据结构中。

接下来问题转化为对每个点，用数据结构维护子节点的权值异或和，要求支持全局 \(+1\) ，单点修改。

看到异或和肯定涉及到 \(\texttt{trie}\) ，而接下来一步则是神来之笔：倒序插入！

我们平常写的字典树都是从高往低走，第一步根据最高位（比如第 \(29\) 位）判断往左还是往右走，以此类推。

本题则刚好反过来，第一步根据最低位判断，以此类推。

这样执行全局 \(+1\) 操作时，只需交换左右儿子，然后递归新的左儿子！

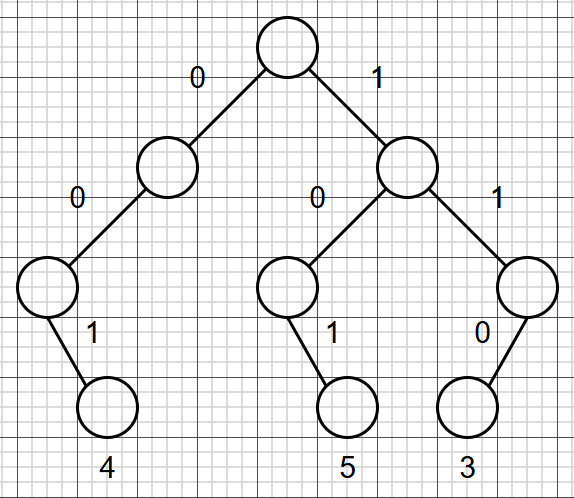
比如上图， \(0\cdot 1+0\cdot 2+1\cdot 4=4\) ， \(1\cdot 1+0\cdot 2+1\cdot 4=5\) ， \(1\cdot 1+1\cdot 2+0\cdot 4=3\) 。

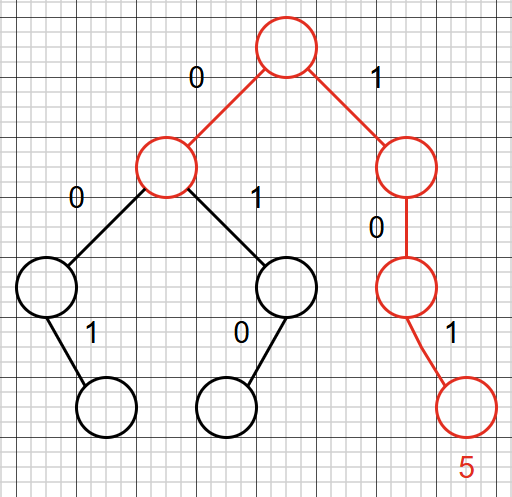
经过第一次交换后， \(4\) 就变成 \(5\) 了。（红色表示已经更新完毕的节点）

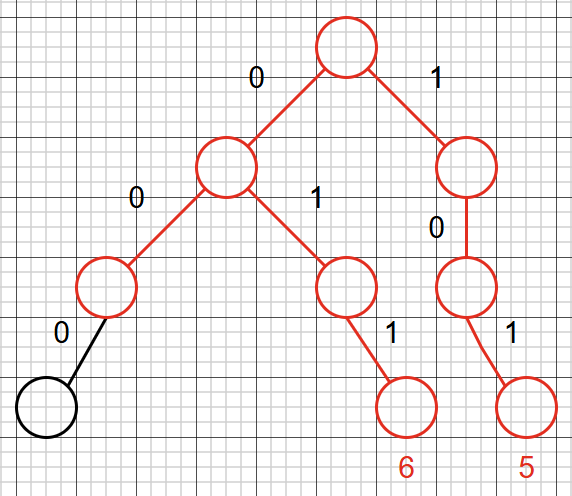
第二次更新后， \(5\) 变成了 \(6\) 。

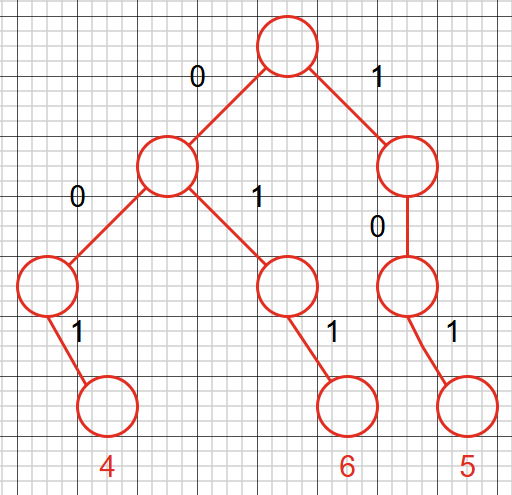
第三次更新后， \(3\) 变成了 \(4\) 。

---

上面展示了全局 \(+1\) 操作的执行过程，而接下来维护异或和就很简单了。对 \(\texttt{trie}\) 上的每个节点维护子树大小、异或和，低位由左右儿子异或得到，高位用右子树大小判断。

时间复杂度 \(\mathcal O((n+m)\log(m+a_i))\) 。

#include<bits/stdc++.h>
using namespace std;
const int maxn=5e5+5,maxm=40*maxn;
int m,n,u,v,tot;
int w[maxn],fa[maxn],rt[maxn],tag[maxn];
vector<int> g[maxn];
int ch[maxm][2],sz[maxm],val[maxm];
void insert(int p,int v,int sgn=1)
{
    for(int i=0;i<20;i++)
    {
        int c=v>>i&1;
        if(!ch[p][c]) ch[p][c]=++tot;
        sz[p]+=sgn,val[p]^=v&~((1<<i)-1);
        p=ch[p][c];
    }
}
void dfs(int u,int f)
{
    for(auto v:g[u]) if(v!=f) fa[v]=u,insert(rt[u],w[v]),dfs(v,u);
}
void update(int p,int d)
{
    if(!p||d==20) return ;
    swap(ch[p][0],ch[p][1]),update(ch[p][0],d+1);
    val[p]=val[ch[p][0]]^val[ch[p][1]]^((sz[ch[p][1]]&1)<<d);
}
int ask(int u)
{
    return w[u]+tag[fa[u]];
}
void modify(int u,int v)
{
    if(!u) return ;
    if(u==1) return w[u]+=v,void();
    ///修改前节点 u 的权值为 w[u]+tag[fa[u]] ,修改后加上 v 
    insert(rt[fa[u]],ask(u),-1),w[u]+=v,insert(rt[fa[u]],ask(u),1);
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n-1;i++) scanf("%d%d",&u,&v),g[u].push_back(v),g[v].push_back(u);
    for(int i=1;i<=n;i++) scanf("%d",&w[i]),rt[i]=++tot;
    dfs(1,0);
    for(int op,x,v;m--;)
    {
        scanf("%d%d",&op,&x);
        if(op==1) tag[x]++,update(rt[x],0),modify(fa[x],1);
        if(op==2) scanf("%d",&v),modify(x,-v);
        if(op==3) printf("%d\n",val[rt[x]]^ask(fa[x]));
    }
    return 0;
}