完全图 MST 小记
一、概述
完全图 \(\texttt{MST}\) (Minimum Spanning Tree,最小生成树)相关题目一般具有以下特征:一张 \(n\) 个点的完全图,第 \(i\) 个点和第 \(j\) 个点之间的边权与这两个点的信息有关。
常见解法有两种:
- 通过题目性质证明大量的边一定不会出现在 \(\texttt{MST}\) 中,保留低于平方量级的边,然后跑 \(\texttt{Kruskal}\) 。
- 使用 \(\texttt{Boruvka}\) 算法,将连通块中的点视为同种颜色,结合题目性质快速求出每个连通块(一般是先对每个点求,再统计到连通块上)的最小异色出边。
二、相关例题
例1、 \(\texttt{ARC076B Built?}\)
题目描述
给定二维平面上的 \(n\) 个点 \((x_i,y_i)\) ,定义 \((a,b),(c,d)\) 两点之间的距离为:
求这 \(n\) 个点构成的最小生成树。
数据范围
- \(2\le n\le 10^5,0\le x_i,y_i\le 10^9\) 。
时间限制 \(\texttt{2s}\) ,空间限制 \(\texttt{256MB}\) 。
分析
可以看成 \((a,b),(c,d)\) 之间有两条边,一条权值为 \(|a-c|\) ,另一条权值为 \(|b-d|\) 。
假设这些点已经按横坐标升序排序,那么我们只需保留相邻两点之间的边。这是因为 \(\forall j-i\gt 1\) , \(w(i,j)=w(i,i+1)+\cdots+w(j-1,j)\) ,用相同的代价可以连接 \([i,j]\) 之间的所有点,因此选这条边一定不优。
纵坐标同理,对这 \(2n-2\) 条边跑 \(\texttt{Kruskal}\) 算法即可,时间复杂度 \(\mathcal O(n\log n)\) 。
#include<bits/stdc++.h>
#define tri array<int,3>
using namespace std;
const int maxn=1e5+5;
int m,n,res;
int f[maxn];
tri a[maxn],e[2*maxn];
int find(int x)
{
return f[x]==x?x:f[x]=find(f[x]);
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d%d",&a[i][0],&a[i][1]),a[i][2]=f[i]=i;
sort(a+1,a+n+1,[&](tri x,tri y){return x[0]<y[0];});
for(int i=2;i<=n;i++) e[++m]={a[i-1][2],a[i][2],a[i][0]-a[i-1][0]};
sort(a+1,a+n+1,[&](tri x,tri y){return x[1]<y[1];});
for(int i=2;i<=n;i++) e[++m]={a[i-1][2],a[i][2],a[i][1]-a[i-1][1]};
sort(e+1,e+m+1,[&](tri x,tri y){return x[2]<y[2];});
for(int i=1;i<=m;i++)
{
int u=find(e[i][0]),v=find(e[i][1]);
if(u!=v) f[u]=v,res+=e[i][2];
}
printf("%d\n",res);
return 0;
}
例2、\(\texttt{BZOJ2177 曼哈顿最小生成树}\)
题目描述
给定二维平面上的 \(n\) 个点 \((x_i,y_i)\) ,定义 \((a,b),(c,d)\) 两点之间的距离为曼哈顿距离:
求这 \(n\) 个点构成的最小生成树。
数据范围
- \(2\le n\le 10^5,0\le x_i,y_i\le 10^9\) 。
时间限制 \(\texttt{2s}\) ,空间限制 \(\texttt{512MB}\) 。
分析
对于任意一个点 \(A\) ,以其为原点,坐标轴和对角线会将整个平面分成 \(8\) 个区域,可以证明每个区域中只需保留离 \(A\) 最近的点与 \(A\) 之间的边。
怎么想到的?
大胆猜测与 \(A\) 相关的有用的边不会太多。假设离 \(A\) 最近的点为 \(B\) ,那么以 \(A\) 为中心, \(B\) 为边(或角)上一点的 \(45\degree\) 摆放的正方形中没有除 \(A\) 以外的点。现在已知 \(|AC|\ge|AB|\) ,如果能够证明 \(|AC|\ge|BC|\) ,那么边 \(AC\) 是没用的。
这等价于某条锯齿线(为方便起见用 \(AB\) 的中垂线拟合这条锯齿线)靠近 \(A\) 一侧的半平面完全包含在正方形中,显然这不可能。但是我们可以给平面添加限制,博主一开始想的是划分成四个象限,以第一象限为例,只需保证半平面与第一象限的交集完全包含在正方形中,但很可惜这还是做不到。再手玩一下就会发现,细化到 \(\frac 18\) 平面就可以做到了。
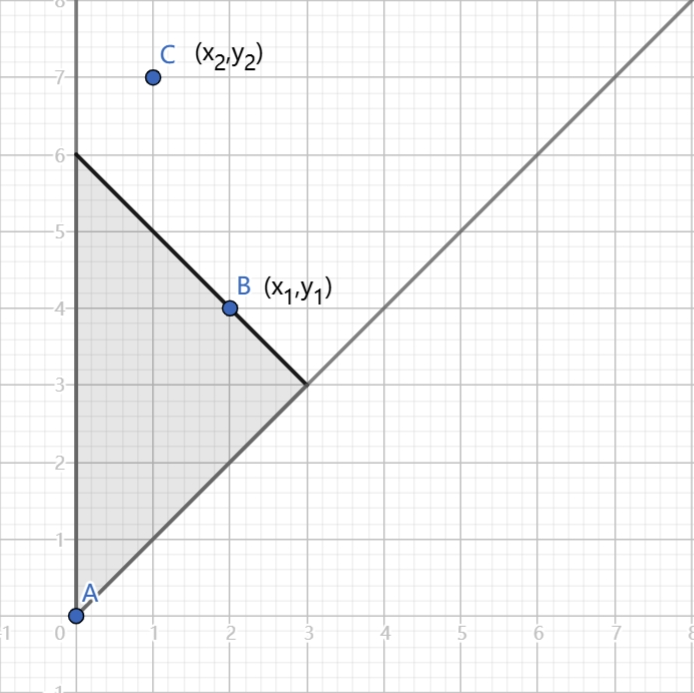
证明:
如上图,灰色区域中没有点,只需证对任意位于夹角中的 \(C\) ,有 \(|AC|\ge|BC|\) 。
设 \(B\) 点坐标为 \((x_1,y_1)\) , \(C\) 点坐标为 \((x_2,y_2)\) ,目标等价于证明 \(|x_2-x_1|+|y_2-y_1|\le x_2+y_2\) 。
已知条件: \(0\le x_1\le y_1,0\le x_2\le y_2,x_1+y_1\le x_2+y_2\) 。
- 如果 \(x_2\ge x_1\) ,则 \(x_2\ge|x_2-x_1|\) ,且由 \(2y_2\ge y_1\) 知 \(y_2\ge|y_2-y_1|\) ,得证。
- 如果 \(x_2\lt x_1\) ,则 \(y_2\gt y_1\) , \(y_2-|y_2-y_1|=y_1\ge x_1\ge|x_2-x_1|\) ,得证。
因此只需保留至多 \(8n\) 条边。
接下来的目标是对每个点 \(A\) 求出最近的 \(B\) ,设 \(A\) 的坐标为 \((x_0,y_0)\) ,以上图所示区域(第一块区域)为例, \(B\) 需要满足:
降序扫描 \(x\) ,树状数组维护 \(y+x\) 的后缀 \(\min\) 即可。
然后令 \((x,y)\to(y+x,y-x)\) ,从而达到让坐标轴顺时针旋转 \(45\degree\) 的目的。注意上述旋转仅用于判断位置关系是否合法,统计答案用的是原始下标,比如第一块区域要维护 \(x_1+y_1\) 的最小值,第二块区域要维护 \(y_1-x_1\) 的最小值,等等。
重复 \(8\) 次即可,时间复杂度 \(\mathcal O(n\log n)\) 。
#include<bits/stdc++.h>
#define fi first
#define se second
#define mp make_pair
#define pii pair<int,int>
using namespace std;
const int maxn=5e4+5,inf=1e9;
int m,n,res;
int c[maxn],f[maxn],x[maxn],y[maxn];
pii t[maxn];
int dx[9]={0,1,-1,-1,-1,-1,1,1,1};
int dy[9]={0,1,1,1,-1,-1,-1,-1,1};
struct node
{
int x,y,w;
}a[maxn];
vector<node> vec;
void addedge(int u,int v)
{
if(u&&v) vec.push_back({u,v,abs(x[u]-x[v])+abs(y[u]-y[v])});
}
int find(int x)
{
return f[x]==x?x:f[x]=find(f[x]);
}
void chmin(pii &a,pii b)
{
if(a>b) a=b;
}
void add(int x,pii v)
{
while(x) chmin(t[x],v),x-=x&-x;
}
pii query(int x)
{
pii res=mp(inf,0);
while(x<=m) chmin(res,t[x]),x+=x&-x;
return res;
}
void work(int id)
{
sort(a+1,a+n+1,[&](node a,node b){return a.x!=b.x?a.x>b.x:a.y>b.y;});
for(int i=1;i<=n;i++) c[i]=a[i].y-a[i].x,t[i]=mp(inf,0);
sort(c+1,c+n+1),m=unique(c+1,c+n+1)-c-1;
for(int i=1;i<=n;i++)
{
int cur=lower_bound(c+1,c+m+1,a[i].y-a[i].x)-c;
addedge(a[i].w,query(cur).se),add(cur,mp(dx[id]*x[a[i].w]+dy[id]*y[a[i].w],a[i].w));
}
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d%d",&x[i],&y[i]),a[i]={x[i],y[i],i},f[i]=i;
for(int i=1;i<=8;i++)
{
work(i);
for(int j=1;j<=n;j++) a[j]={a[j].y+a[j].x,a[j].y-a[j].x,a[j].w};
if(i%2==0) for(int j=1;j<=n;j++) a[j].x/=2,a[j].y/=2;
}
sort(vec.begin(),vec.end(),[&](node a,node b){return a.w<b.w;});
for(auto e:vec)
{
int u=find(e.x),v=find(e.y),w=e.w;
if(u!=v) f[u]=v,res+=w;
}
printf("%d\n",res);
return 0;
}
例3、\(\texttt{CF103118B Build Roads}\)
题目描述
给定一个长为 \(n\) 的数组 \(a\) , \(a_i\) 在 \([l,r]\) 中随机生成。
第 \(i\) 个点和第 \(j\) 个点的边权为 \(\gcd(a_i,a_j)\) ,求最小生成树。
数据范围
- \(2\le n\le 2\cdot 10^5,1\le l\le r\le 2\cdot 10^5\) 。
时间限制 \(\texttt{2s}\) ,空间限制 \(\texttt{256MB}\) 。
分析
大胆猜测 \(n\) 很大时答案为 \(n-1\) 。
因此对 \(n\le 1000\) ,直接跑 \(\texttt{Kruskal}\) 算法;对 \(n\gt 1000\) ,直接输出 \(n-1\) 即可。
别忘了特判 \(l=r\) 的情况,此时答案为 \((n-1)\cdot l\) 。
#include<bits/stdc++.h>
using namespace std;
const int maxn=5e5+5;
int l,r,m,n,res;
unsigned long long x,a[maxn];
int f[maxn];
struct edge
{
int u,v,w;
}e[maxn];
int rnd()
{
x^=x<<13,x^=x>>7,x^=x<<17;
return l+x%(r-l+1);
}
int find(int x)
{
return f[x]==x?x:f[x]=find(f[x]);
}
int main()
{
scanf("%d%d%d%llu",&n,&l,&r,&x);
for(int i=1;i<=n;i++) a[i]=rnd();
if(l==r) printf("%lld\n",(n-1ll)*l),exit(0);
if(n>1000) printf("%d\n",n-1),exit(0);
for(int i=1;i<=n;i++) f[i]=i;
for(int i=1;i<=n;i++)
for(int j=i+1;j<=n;j++)
e[++m]={i,j,(int)__gcd(a[i],a[j])};
sort(e+1,e+m+1,[&](edge a,edge b){return a.w<b.w;});
for(int i=1;i<=m;i++)
{
int u=find(e[i].u),v=find(e[i].v);
if(u!=v) f[u]=v,res+=e[i].w;
}
printf("%d\n",res);
return 0;
}
例4、\(\texttt{P8207 [THUPC 2022 初赛] 最小公倍树}\)
题目描述
定义 \(u,v\) 两点之间的距离为 \(\text{lcm}(u,v)\) ,求由点 \(l,\cdots,r\) 构成的最小生成树。
数据范围
- \(1\le l\le r\le 10^6,r-l\le 10^5\) 。
时间限制 \(\texttt{1s}\) ,空间限制 \(\texttt{512MB}\) 。
分析
可以看成 \(\forall d\mid\gcd(u,v)\) ,在 \((u,v)\) 两点之间连有权值为 \(\frac{uv}d\) 的边。
反过来等价于, \(\forall 1\le d\le r\) ,考虑所有 \(d\) 的倍数的点,在 \((u,v)\) 两点之间连有权值 \(\frac{uv}d\) 的边。
记 \([l,r]\) 中第一个 \(d\) 的倍数为 \(x\) ,显然只需保留所有 \((u,x)\) 边,这样的边共有 \(\mathcal O(\frac{r-l}d)\) 条。
因此总边数为调和级数 \(\mathcal O((r-l)\log(r-l))\) ,建图后跑 \(\texttt{Kruskal}\) 算法,时间复杂度 \(\mathcal O((r-l)\log^2(r-l))\) 。
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=2e6+5;
int l,m,r;
ll res;
int f[maxn];
struct node
{
int u,v;
ll w;
}e[maxn];
int find(int x)
{
return f[x]==x?x:f[x]=find(f[x]);
}
int main()
{
scanf("%d%d",&l,&r);
for(int d=1;d<=r;d++)
for(int x=((l-1)/d+1)*d,i=x+d;i<=r;i+=d)
e[++m]={x,i,1ll*x*i/d};
for(int i=l;i<=r;i++) f[i]=i;
sort(e+1,e+m+1,[&](node x,node y){return x.w<y.w;});
for(int i=1;i<=m;i++)
{
int u=find(e[i].u),v=find(e[i].v);
if(u!=v) f[u]=v,res+=e[i].w;
}
printf("%lld\n",res);
return 0;
}
例5、\(\texttt{CF888G Xor-MST}\)
题目描述
给定长为 \(n\) 的数组 \(a_i\) ,第 \(i\) 个点和第 \(j\) 个点之间的边权为 \(a_i\oplus a_j\) ,求最小生成树。
数据范围
- \(1\le n\le 2\cdot 10^5,0\le a_i\lt 2^{30}\) 。
时间限制 \(\texttt{2s}\) ,空间限制 \(\texttt{256MB}\) 。
分析
模拟 \(\texttt{Kruskal}\) 算法的流程,每次找权值最小的边,而权值最小等价于在 \(\texttt{trie}\) 上 \(\texttt{lca}\) 深度尽可能大。
因此按照在 \(\texttt{trie}\) 上 \(dfs\) 的顺序合并一定没错,如果只有 \(1\) 个儿子则直接递归;否则从左右子树中分别选一个点,并且在 \(\texttt{MST}\) 中添加这两点之间的边。
将 \(a\) 升序排序,则 \(\texttt{trie}\) 上每个节点对应 \(a\) 中的一个区间。枚举左子树中的每个元素,去右子树查询最小异或值即可。
每个元素最多需要查 \(\log V\) 次,每次查询代价 \(\log V\) ,时间复杂度 \(\mathcal O(n\log^2V)\) 。
#include<bits/stdc++.h>
using namespace std;
const int maxn=2e5+5,maxm=6e6+5;
int n,tot;
long long res;
int a[maxn],ch[maxm][2],l[maxm],r[maxm];
int query(int x,int p,int dep)
{
int res=0;
for(int i=dep;i>=0;i--)
{
int k=x>>i&1;
if(ch[p][k]) p=ch[p][k];
else res+=1<<i,p=ch[p][k^1];
}
return res;
}
void dfs(int p,int dep)
{
if(dep==-1) return ;
if(ch[p][0]) dfs(ch[p][0],dep-1);
if(ch[p][1]) dfs(ch[p][1],dep-1);
if(ch[p][0]&&ch[p][1])
{
int cur=INT_MAX;
for(int i=l[ch[p][0]];i<=r[ch[p][0]];i++) cur=min(cur,query(a[i],ch[p][1],dep-1));
res+=cur+(1<<dep);
}
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
sort(a+1,a+n+1);
for(int i=1;i<=n;i++)
for(int j=29,p=0;j>=0;j--)
{
int k=a[i]>>j&1;
if(!ch[p][k]) ch[p][k]=++tot,l[tot]=i;
p=ch[p][k],r[p]=i;
}
dfs(0,29);
printf("%lld\n",res);
return 0;
}
例6、\(\texttt{P7789 [COCI 2016/2017 \#6] Sirni}\)
题目描述
给定长为 \(n\) 的数组 \(p_i\) ,第 \(i\) 个点和第 \(j\) 个点之间的距离为 \(\min(p_i\bmod p_j,p_j\bmod p_i)\) ,求最小生成树。
数据范围
- \(1\le n\le 10^5,1\le p_i\le 10^7\) 。
时间限制 \(\texttt{5s}\) ,空间限制 \(\texttt{800MB}\) 。
分析
显然相同的 \(p\) 没有意义,升序排序后去重,对于 \(i\lt j\) ,第 \(i\) 个点和第 \(j\) 个点之间的距离为 \(p_j\bmod p_i\) 。
固定模数 \(d\) ,则 \(\big[kd,(k+1)d\big)\) 之间只有第一个数连向 \(d\) 的边是有用的。
这是因为对于 \(p_a=d,p_b=kd+r_1,p_c=kd+r_2\) ,有:
这样总边数不超过 \(m=\sum_{i=1}^n\min(n-i,\frac Vi)=78967794\) ,但是显然远远卡不满,最后跑一次 \(\texttt{Kruskal}\) 算法即可。
时间复杂度 \(\mathcal O(m\log m)\) 。
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+5;
int m,n,res;
int a[maxn],f[maxn];
struct edge
{
int u,v,w;
}e[500*maxn];
int find(int x)
{
return f[x]==x?x:f[x]=find(f[x]);
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
sort(a+1,a+n+1),n=unique(a+1,a+n+1)-a-1;
for(int i=1;i<=n;i++)
for(int d=a[i],j=i+1,x=d;;x+=d)
{
while(j<=n&&a[j]<x) j++;
if(j==n+1) break;
if(a[j]<x+d) e[++m]={i,j,a[j]-x};
}
for(int i=1;i<=n;i++) f[i]=i;
sort(e+1,e+m+1,[&](edge a,edge b){return a.w<b.w;});
for(int i=1;i<=m;i++)
{
int u=find(e[i].u),v=find(e[i].v);
if(u!=v) f[u]=v,res+=e[i].w;
}
printf("%d\n",res);
return 0;
}
例7、\(\texttt{AT cf17\_final\_j Tree MST}\)
题目描述
给定一个长为 \(n\) 的数组 \(x\) 和一棵 \(n\) 个点的树,边有边权。
构造一张新的完全图,第 \(i\) 个点和第 \(j\) 个点之间的边权为:
对这张完全图求最小生成树。
数据范围
- \(2\le n\le 2\cdot 10^5\) 。
- \(1\le x_i\le 10^9\) 。
- \(1\le u\neq v\le n,1\le w\le 10^9\) 。
时间限制 \(\texttt{5s}\) ,空间限制 \(\texttt{256MB}\) 。
分析
法一
通过点分治删除多余的边,可以证明如果一条边没有出现在局部最优解中,那么它一定不会出现在全局最优解中。
对点分治得到的连通块求 \(\texttt{MST}\) ,令 \(p_u=x_u+dis(rt,u)\) ,则对于任意在 \(rt\) 不同子树中的两点 \(u,v\) ,它们在完全图中的距离为 \(p_u+p_v\) 。
进一步,我们没有必要限制 \(u,v\) 一定在不同子树中,因为 \(u,v\) 在相同子树意味着 \(dis(u,v)\) 算大了,后续点分治过程中总会处理真实的 \(dis(u,v)\) 。
此时的 \(\texttt{MST}\) 结构非常简单,所有点连向 \(p\) 最小的点即可,我们会得到 \(\mathcal O(sz)\) 条边。
根据点分治的性质,\(\sum sz=\mathcal O(n\log n)\) 。
最后用这些边跑 \(\texttt{Kruskal}\) 算法,时间复杂度 \(\mathcal O(n\log^2n)\) 。
#include<bits/stdc++.h>
#define ll long long
#define fi first
#define se second
#define mp make_pair
#define pii pair<ll,int>
using namespace std;
const int maxn=2e5+5,inf=1e9;
int m,n,rt,cnt,sum,tot;
ll res;
int f[maxn],w[maxn];
int head[maxn],to[2*maxn],val[2*maxn],nxt[2*maxn];
int dp[maxn],sz[maxn];
bool vis[maxn];
pii p[maxn];
struct edge
{
int u,v;
ll w;
}e[20*maxn];
bool cmp(edge a,edge b)
{
return a.w<b.w;
}
void addedge(int u,int v,int w)
{
nxt[++tot]=head[u],to[tot]=v,val[tot]=w,head[u]=tot;
}
void getroot(int u,int fa)
{
dp[u]=0,sz[u]=1;
for(int i=head[u];i;i=nxt[i])
{
int v=to[i];
if(vis[v]||v==fa) continue;
getroot(v,u);
dp[u]=max(dp[u],sz[v]),sz[u]+=sz[v];
}
dp[u]=max(dp[u],sum-sz[u]);
if(dp[u]<dp[rt]) rt=u;
}
void dfs(int u,int fa,ll dis)
{
p[++cnt]=mp(w[u]+dis,u);
for(int i=head[u];i;i=nxt[i])
{
int v=to[i];
if(vis[v]||v==fa) continue;
dfs(v,u,dis+val[i]);
}
}
void calc(int u)
{
cnt=0,dfs(u,0,0),sort(p+1,p+cnt+1);
for(int i=2;i<=cnt;i++) e[++m]={p[1].se,p[i].se,p[1].fi+p[i].fi};
}
void solve(int u)
{
vis[u]=true,calc(u);
for(int i=head[u];i;i=nxt[i])
{
int v=to[i];
if(vis[v]) continue;
sum=sz[v],getroot(v,rt=0);
solve(rt);
}
}
int find(int x)
{
if(f[x]==x) return x;
return f[x]=find(f[x]);
}
void kruskal()
{
sort(e+1,e+m+1,cmp);
for(int i=1;i<=n;i++) f[i]=i;
for(int i=1;i<=m;i++)
{
int u=find(e[i].u),v=find(e[i].v);
if(u==v) continue;
f[u]=v,res+=e[i].w;
}
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&w[i]);
for(int i=1,u,v,w;i<=n-1;i++)
{
scanf("%d%d%d",&u,&v,&w);
addedge(u,v,w),addedge(v,u,w);
}
sum=n,dp[rt=0]=inf,getroot(1,0);
solve(rt),kruskal();
printf("%lld\n",res);
return 0;
}
法二
考虑 \(\texttt{Boruvka}\) 算法,每一轮对每个点 \(i\) ,维护 \(x_j+dis_T(i,j)\) 的最小值。
这个问题可以通过两次 \(dfs\) 解决,第一次统计子树内的 \(j\) 的贡献,第二次统计子树外的 \(j\) 的贡献。
由于我们还要保证 \(i,j\) 在不同连通块中,维护最小值和颜色不同的次小值即可。
时间复杂度 \(\mathcal O(n\log n)\) ,但是跑得比 \(2\log\) 的点分治慢不少。
#include<bits/stdc++.h>
#define int long long
#define fi first
#define se second
#define mp make_pair
#define pii pair<int,int>
using namespace std;
const int maxn=2e5+5,inf=1e18;
const pii o=mp(inf,0);
int n,u,v,w,res;
int f[maxn],x[maxn];
vector<pii> e[maxn];
pair<pii,pii> g[maxn],h[maxn],q[maxn];
void tran(pair<pii,pii> &p,vector<pii> v,int x)
{
for(auto &p:v) p.fi+=x;
v.push_back(p.fi),v.push_back(p.se);
sort(v.begin(),v.end()),p.fi=v[0];
for(int i=1;i<v.size();i++) if(v[i].se!=v[0].se) return p.se=v[i],void();
}
int find(int x)
{
return f[x]==x?x:f[x]=find(f[x]);
}
void dfs1(int u,int fa)
{
g[u]={mp(x[u],find(u)),o};
for(auto [v,w]:e[u])
{
if(v==fa) continue;
dfs1(v,u),tran(g[u],{g[v].fi,g[v].se,mp(x[v],find(v))},w);
}
}
void dfs2(int u,int fa)
{
tran(h[u],{mp(x[u],find(u))},0);
pair<pii,pii> tmp=h[u];
for(int i=0;i<e[u].size();i++)
{
auto [v,w]=e[u][i];
if(v==fa) continue;
tran(h[v],{tmp.fi,tmp.se},w),tran(tmp,{g[v].fi,g[v].se},w);
}
tmp={o,o};
for(int i=(int)(e[u].size())-1;i>=0;i--)
{
auto [v,w]=e[u][i];
if(v==fa) continue;
tran(h[v],{tmp.fi,tmp.se},w),tran(tmp,{g[v].fi,g[v].se},w);
}
for(auto [v,w]:e[u]) if(v!=fa) dfs2(v,u);
}
signed main()
{
scanf("%lld",&n);
for(int i=1;i<=n;i++) scanf("%lld",&x[i]),f[i]=i;
for(int i=1;i<=n-1;i++)
{
scanf("%lld%lld%lld",&u,&v,&w);
e[u].push_back(mp(v,w)),e[v].push_back(mp(u,w));
}
while(true)
{
int cnt=0;
for(int i=1;i<=n;i++) cnt+=find(i)==i,g[i]=h[i]={o,o},q[i]={o,o};
if(cnt==1) break;
dfs1(1,0),dfs2(1,0);
for(int i=1;i<=n;i++) tran(q[find(i)],{g[i].fi,g[i].se,h[i].fi,h[i].se},x[i]);
for(int i=1;i<=n;i++)
{
if(q[i]==mp(o,o)) continue;
auto [v,w]=q[i].fi.se!=i?q[i].fi:q[i].se;
if(w&&find(w)!=find(i)) res+=v,f[find(i)]=find(w);
}
}
printf("%lld\n",res);
return 0;
}
例8、\(\texttt{P6199 [EER1] 河童重工}\)
题目描述
给定两棵 \(n\) 个点的树 \(T_1,T_2\) ,定义第 \(i\) 个点和第 \(j\) 个点之间的距离为 \(dis_{T_1}(i,j)+dis_{T_2}(i,j)\) ,求最小生成树。
数据范围
- \(1\le n\le 10^5\) 。
- \(1\le u\neq v\le n,1\le w\le 5000\) 。
时间限制 \(\texttt{4s}\) ,空间限制 \(\texttt{500MB}\) 。
分析
对第二棵树点分治,核心思路是保留每个连通块的 \(\texttt{MST}\) ,对这 \(\sum(sz-1)=\mathcal O(n\log n)\) 条边最后再跑一遍 \(\texttt{Kruskal}\) 。
如果 \(u,v\) 位于 \(rt\) 的不同子树,则 \(dis_{T_2}(u,v)=dep_u+dep_v\) ,同上题我们可以忽略不同子树的限制。
对于这 \(sz\) 个点, \(u,v\) 之间的距离为 \(dep_u+dep_v+dis_{T_1}(u,v)\) ,建立虚树,将虚点的 \(dep\) 设为 \(\infty\) ,那么求 \(\texttt{MST}\) 刚好是上一道题干的事情。
时间复杂度 \(\mathcal O(\sum sz\log sz)=\mathcal O(n\log^2n)\) 。
#include<bits/stdc++.h>
#define ll long long
#define fi first
#define se second
#define mp make_pair
#define pii pair<int,int>
using namespace std;
const int maxn=1e5+5,inf=1e9;
int n,u,v,w;
int dep[maxn];
struct edge
{
int u,v,w;
}e[20*maxn];
vector<edge> vec;
namespace t1
{
int m,rt,all,cnt;
int c[maxn],d[maxn],fa[maxn],sz[maxn],son[maxn];
int dfn[maxn],top[maxn];
int f[maxn],mx[maxn],st[maxn];
vector<int> del;
vector<pii> g[maxn],h[maxn];
bitset<maxn> vis;
pii p[maxn];
///树剖lca
void dfs1(int u,int f)
{
sz[u]=1;
for(auto [v,w]:g[u])
{
if(v==f) continue;
c[v]=c[u]+w,d[v]=d[u]+1,fa[v]=u,dfs1(v,u),sz[u]+=sz[v];
if(sz[v]>=sz[son[u]]) son[u]=v;
}
}
void dfs2(int u,int f)
{
dfn[u]=++cnt,top[u]=f;
if(son[u]) dfs2(son[u],f);
for(auto [v,w]:g[u])
{
if(v==fa[u]||v==son[u]) continue;
dfs2(v,v);
}
}
int lca(int u,int v)
{
while(top[u]!=top[v])
{
if(d[top[u]]<d[top[v]]) swap(u,v);
u=fa[top[u]];
}
return d[u]<d[v]?u:v;
}
void init()
{
for(int i=1;i<=n;i++) f[i]=i,dep[i]=inf;
d[1]=1,dfs1(1,0),dfs2(1,1);
}
///树剖结束
void addedge(int u,int v)
{
int w=c[v]-c[u];
h[u].push_back(mp(v,w)),h[v].push_back(mp(u,w)),all++;
}
///第二次点分治
void getroot(int u,int fa)
{
sz[u]=1,mx[u]=0;
for(auto [v,w]:h[u])
{
if(vis[v]||v==fa) continue;
getroot(v,u),sz[u]+=sz[v],mx[u]=max(mx[u],sz[v]);
}
mx[u]=max(mx[u],all-sz[u]);
if(!rt||mx[u]<mx[rt]) rt=u;
}
void dfs(int u,int fa,int cur)
{
if(dep[u]!=inf) p[++cnt]=mp(dep[u]+cur,u);
for(auto [v,w]:h[u])
{
if(vis[v]||v==fa) continue;
dfs(v,u,cur+w);
}
}
void calc(int u)
{
cnt=0,dfs(u,0,0),sort(p+1,p+cnt+1);
for(int i=2;i<=cnt;i++) e[++m]={p[1].se,p[i].se,p[1].fi+p[i].fi};
}
void solve(int u)
{
del.push_back(u),vis[u]=1,calc(u);
for(auto [v,w]:h[u])
{
if(vis[v]) continue;
all=sz[v],getroot(v,rt=0),solve(rt);
}
}
///点分治结束
int find(int x)
{
return f[x]==x?x:f[x]=find(f[x]);
}
void work(vector<int> poi)
{
m=0,all=1;
///建立虚树
sort(poi.begin(),poi.end(),[&](int x,int y){return dfn[x]<dfn[y];});
int top=1;st[1]=1,h[1].clear();
for(auto u:poi)
{
if(u==1) continue;
int p=lca(u,st[top]);
if(p!=st[top])
{
while(dfn[p]<dfn[st[top-1]]) addedge(st[top-1],st[top]),top--;
if(dfn[p]>dfn[st[top-1]]) h[p].clear(),addedge(p,st[top--]),st[++top]=p;
else addedge(st[top-1],st[top]),top--;
}
h[u].clear(),st[++top]=u;
}
while(top>=2) addedge(st[top-1],st[top]),top--;
///点分治+kruskal求MST
getroot(1,rt=0),solve(rt);
sort(e+1,e+m+1,[&](edge a,edge b){return a.w<b.w;});
for(int i=1;i<=m;i++)
{
int u=find(e[i].u),v=find(e[i].v);
if(u!=v) f[u]=v,vec.push_back(e[i]);
}
for(auto u:del) f[u]=u,dep[u]=inf,vis[u]=0;
del.clear();
}
}
namespace t2
{///第一次点分治
int rt,all;
long long res;
int f[maxn],mx[maxn],sz[maxn];
bitset<maxn> vis;
vector<pii> g[maxn];
vector<int> poi;
void getroot(int u,int fa)
{
sz[u]=1,mx[u]=0;
for(auto [v,w]:g[u])
{
if(vis[v]||v==fa) continue;
getroot(v,u),sz[u]+=sz[v],mx[u]=max(mx[u],sz[v]);
}
mx[u]=max(mx[u],all-sz[u]);
if(!rt||mx[u]<mx[rt]) rt=u;
}
void dfs(int u,int fa)
{
poi.push_back(u);
for(auto [v,w]:g[u])
{
if(vis[v]||v==fa) continue;
dep[v]=dep[u]+w,dfs(v,u);
}
}
void solve(int u)
{
poi.clear(),dfs(u,dep[u]=0),t1::work(poi);
vis[u]=1;
for(auto [v,w]:g[u])
{
if(vis[v]) continue;
all=sz[v],getroot(v,rt=0),solve(rt);
}
}
int find(int x)
{
return f[x]==x?x:f[x]=find(f[x]);
}
void work()
{
all=n,getroot(1,0),solve(rt);
for(int i=1;i<=n;i++) f[i]=i;
sort(vec.begin(),vec.end(),[&](edge a,edge b){return a.w<b.w;});
for(auto [u,v,w]:vec)
{
u=find(u),v=find(v);
if(u!=v) f[u]=v,res+=w;
}
printf("%lld\n",res);
}
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n-1;i++)
{
scanf("%d%d%d",&u,&v,&w);
t1::g[u].push_back(mp(v,w)),t1::g[v].push_back(mp(u,w));
}
for(int i=1;i<=n-1;i++)
{
scanf("%d%d%d",&u,&v,&w);
t2::g[u].push_back(mp(v,w)),t2::g[v].push_back(mp(u,w));
}
t1::init(),t2::work();
return 0;
}
例9、\(\texttt{P9701/CF104369L [GDCPC2023] Classic Problem}\)
题目描述
\(T\) 组数据,给定 \(n\) 个点的无向完全图和 \(m\) 个三元组 \(P_i=(u_i,v_i,w_i)\) 。
对于无向完全图中的任意两个节点 \(1\le x\lt y\le n\) :
- 如果存在 \(P_i\) 满足 \(u_i=x,v_i=y\) ,则边权为 \(w_i\) 。
- 否则边权为 \(y-x\) 。
求这张图的最小生成树。
数据范围
- \(1\le T\le 10^5,1\le n\le 10^9,0\le m\le 10^5,\sum m\le 5\cdot 10^5\) 。
- \(1\le u_i\lt v_i\le n,0\le w_i\le 10^9\) ,保证 \(i\neq j\) 时, \((u_i,v_i)\neq(u_j,v_j)\) 。
时间限制 \(\texttt{8s}\) ,空间限制 \(\texttt{1GB}\) 。
分析
提取 \(2m\) 个关键点,它们会将 \([1,n]\) 分割成至多 \(4m+1\) 个区间。
假设总共有 \(k\) 个区间 \([l_1,r_1],\cdots,[l_k,r_k]\) 。
考虑 \(\texttt{boruvka}\) 算法,对每个区间求最小出边。
特殊边是容易的,将所有特殊边按照 \(w\) 排序,如果最小的 \((v,w)\) 满足 \(u,v\) 同色,将这条边删去即可。
对于普通边,当 \(i\lt j\) 时,第 \(i\) 个和第 \(j\) 个区间的距离为 \(l_j-r_i\) ,但是有 \(m\) 条边被 ban 了。
因此问题转化为,对 \(\forall 1\le i\le k\) ,求两侧最近的颜色不同且没被 ban 的区间。
以左侧为例,预处理 \(pre_i\) 表示 \(i\) 左侧第一个与 \(i\) 颜色不同的区间,然后执行以下操作:
- 如果 \(j\) 与 \(i\) 颜色相同,令 \(j\gets pre_j\) 。
- 如果 \((j,i)\) 被 ban ,令 \(j\gets j-1\) 。
- 否则 \(j\) 即为所求。
由于每条边 \((u,v,w)\) 至多只会让 \(v\) 增加一次第二类跳法,而第一类跳法不会连续出现,因此每一轮跳的次数为 \(\mathcal O(m)\) 。
时间复杂度 \(\mathcal O(m\log m)\) 。
冷知识:用
vector加二分判断某个点是否被 ban 比unordered_set快一倍。
#include<bits/stdc++.h>
#define fi first
#define se second
#define mp make_pair
#define pii pair<int,int>
using namespace std;
const int maxn=4e5+5,inf=1e9+5;
int d,k,m,n,t;
long long res;
int c[maxn],f[maxn],l[maxn],r[maxn],pre[maxn],suf[maxn];
pii p[maxn];
vector<pii> vec[maxn];///vec[u]存储(w,v)
unordered_set<int> s[maxn];///s[u]存储被ban的v
struct edge
{
int u,v,w;
}o[maxn];
int find(int x)
{
return f[x]==x?x:f[x]=find(f[x]);
}
void chmin(pii &x,pii y)
{
if(x>y) x=y;
}
void work()
{
scanf("%d%d",&n,&m),d=k=res=0;
for(int i=1;i<=m;i++) scanf("%d%d%d",&o[i].u,&o[i].v,&o[i].w),c[++d]=o[i].u,c[++d]=o[i].v;
sort(c+1,c+d+1),d=unique(c+1,c+d+1)-c-1;
for(int i=1;i<=d;i++)
{
if(c[i]-c[i-1]>=2) k++,l[k]=c[i-1]+1,r[k]=c[i]-1,res+=r[k]-l[k];
k++,l[k]=r[k]=c[i];
}
if(c[d]!=n) k++,l[k]=c[d]+1,r[k]=n,res+=r[k]-l[k];
f[0]=pre[0]=0,f[k+1]=suf[k+1]=k+1;
for(int i=1;i<=k;i++) f[i]=i,vec[i].clear(),s[i].clear();
for(int i=1;i<=m;i++)
{
int u=lower_bound(l+1,l+k+1,o[i].u)-l,v=lower_bound(l+1,l+k+1,o[i].v)-l,w=o[i].w;
vec[u].push_back(mp(w,v)),s[u].insert(v);
vec[v].push_back(mp(w,u)),s[v].insert(u);
}
for(int i=1;i<=k;i++) sort(vec[i].begin(),vec[i].end(),greater<pii>());
while(true)
{
int cnt=0;
for(int i=1;i<=k;i++) cnt+=find(i)==i,p[i]=mp(inf,0);
if(cnt==1) break;
for(int i=1;i<=k;i++) pre[i]=find(i)==find(i-1)?pre[i-1]:i-1;
for(int i=k;i>=1;i--) suf[i]=find(i)==find(i+1)?suf[i+1]:i+1;
for(int i=1;i<=k;i++)
{
///特殊边
while(!vec[i].empty())
if(find(i)==find(vec[i].back().se)) vec[i].pop_back();
else break;
if(!vec[i].empty()) chmin(p[find(i)],vec[i].back());
///普通边
if(i!=1) for(int j=i-1;j>=1;)
{
if(find(j)==find(i)) j=pre[j];
else if(s[i].count(j)) j--;
else chmin(p[find(i)],mp(l[i]-r[j],j)),j=0;
}
if(i!=k) for(int j=i+1;j<=k;)
{
if(find(j)==find(i)) j=suf[j];
else if(s[i].count(j)) j++;
else chmin(p[find(i)],mp(l[j]-r[i],j)),j=k+1;
}
}
for(int i=1;i<=k;i++)
{
if(p[i]==mp(inf,0)) continue;
int u=find(i),v=find(p[i].se);
if(u!=v) f[u]=v,res+=p[i].fi;
}
}
printf("%lld\n",res);
}
int main()
{
for(scanf("%d",&t);t--;) work();
return 0;
}
本文来自博客园,作者:peiwenjun,转载请注明原文链接:https://www.cnblogs.com/peiwenjun/p/18692897


 浙公网安备 33010602011771号
浙公网安备 33010602011771号