CSP 2021 提高组 题解
A.廊桥分配
题目描述
\(n\) 个廊桥, \(m_1\) 架国内飞机和国外飞机,给定每架飞机的到达和离开时间 \((l_i,r_i)\) 。
你需要将这 \(n\) 个廊桥划分成国内区域和国外区域。如果一架飞机到达,并且对应区域有空着的廊桥,那么它会使用这个廊桥。
求所有划分方案中,能够使用廊桥的飞机数量的最大值。
数据范围
- \(1\le n\le10^5\) 。
- \(1\le m_1+m_2\le 10^5\) 。
- \(1\le l_i\lt r_i\le 10^8\) ,保证 \(l_i\) 互不相同。
时间限制 \(\texttt{1s}\) ,空间限制 \(\texttt{512MB}\) 。
分析
预处理 \(a_i,b_i\) 表示分配 \(i\) 个廊桥时,国内或国际能有多少飞机使用廊桥,那么答案为 \(\max\limits_{0\le i\le n}a_i+b_{n-i}\) 。
计算 \(a_i\) 时,前 \(i-1\) 个廊桥的飞机不会有任何变化,我们只需计算新开的廊桥的贡献。
用 set 存储所有飞机,二分求出大于等于 \(r_i\) 的最小 \(l_j\) ,然后将其删除即可。
时间复杂度 \(\mathcal O(n+m_1\log m_1+m_2\log m_2)\) 。
#include<bits/stdc++.h>
#define fi first
#define se second
#define mp make_pair
#define pii pair<int,int>
using namespace std;
const int maxn=1e5+5;
int l,m1,m2,n,r,res;
int a[maxn],b[maxn];
void work(int m,int *f)
{
set<pii> s;
while(m--) scanf("%d%d",&l,&r),s.insert(mp(l,r));
for(int i=1,cnt=0;i<=n;i++)
{
auto it=s.begin();
while(it!=s.end())
{
int r=(*it).se;
cnt++,s.erase(it),it=s.lower_bound(mp(r,0));
}
f[i]=cnt;
}
}
int main()
{
scanf("%d%d%d",&n,&m1,&m2);
work(m1,a),work(m2,b);
for(int i=0;i<=n;i++) res=max(res,a[i]+b[n-i]);
printf("%d\n",res);
return 0;
}
B.括号序列
题目描述
给定常数 \(k\) ,超级括号序列定义如下:
(),(S)为超级括号序列,其中S为由不超过 \(k\) 个*组成的字符串。- 若
A,B均为超级括号序列,则AB,ASB均为超级括号序列。 - 若
A为超级括号序列,则(A),(SA),(AS)均为超级括号序列。
给定长为 \(n\) ,由 (,),*,? 的字符串 \(s\) ,你可以将 ? 替换成其他任意字符,求能得到的超级括号序列的个数,对\(10^9+7\)取模。
数据范围
- \(1\le k\le n\le 500\) 。
时间限制 \(\texttt{1s}\) ,空间限制 \(\texttt{512MB}\) 。
分析
区间 \(\texttt{dp}\) ,容易发现超级括号序列必须是括号序列,考虑用剥括号的方法实现转移。
超级括号序列有如下几个括号序列片段:
A:一个超级括号序列。S:由不超过 \(k\) 个*组成的字符串。AS:左端(属于某个超级括号序列,右端是若干个*,如()*。SA:左端是若干个*,右端)属于某个超级括号序列,如*()。ASA:两端都属于某个超级括号序列(包含第一种情况),如()*()。SAS:两端都是若干个*(包含第二种情况),如*()*。
记 \(f_{l,r,0\sim 5}\) 表示区间 \([l,r]\) 构成上述第 \(i\) 个片段的方案数。
再来考虑转移:
A:首先 \(s_l,s_r\) 必须分别为左右括号,剥掉这对括号后内部可以为S,AS,SA,ASA。S:这个随便判断一下就行了。AS:枚举左端的A,右端剩下AS,SAS。SA:枚举左端的S,右端剩下ASA。ASA:枚举左端的A,右端剩下ASA,SA,记得加上第一种情况的贡献。SAS:枚举左端的S,右端剩下AS,记得加上第二种情况的贡献。
时间复杂度 \(\mathcal O(n^3)\) 。
#include<bits/stdc++.h>
using namespace std;
const int maxn=505,mod=1e9+7;
int k,n;
char s[maxn];
int f[maxn][maxn][6];
inline bool check(int i,char c)
{
return s[i]=='?'||s[i]==c;
}
inline void add(int &x,int y)
{
if((x+=y)>=mod) x-=mod;
}
int main()
{
scanf("%d%d%s",&n,&k,s+1);
for(int i=1;i<=n+1;i++) f[i][i-1][1]=1;
for(int l=n;l>=1;l--)
for(int r=l;r<=n;r++)
{
if(check(l,'(')&&check(r,')')) for(int i=1;i<=4;i++) add(f[l][r][0],f[l+1][r-1][i]);
f[l][r][1]=r-l+1<=k&&f[l][r-1][1]&&check(r,'*');
for(int i=l;i<r;i++)
{
f[l][r][2]=(f[l][r][2]+1ll*f[l][i][0]*(f[i+1][r][2]+f[i+1][r][5]))%mod;
f[l][r][3]=(f[l][r][3]+1ll*f[l][i][1]*f[i+1][r][4])%mod;
f[l][r][4]=(f[l][r][4]+1ll*f[l][i][0]*(f[i+1][r][4]+f[i+1][r][3]))%mod;
f[l][r][5]=(f[l][r][5]+1ll*f[l][i][1]*f[i+1][r][2])%mod;
}
add(f[l][r][4],f[l][r][0]),add(f[l][r][5],f[l][r][1]);
}
printf("%d\n",f[1][n][4]);
return 0;
}
C.回文
题目描述
\(T\) 组数据,给定长为 \(2n\) 的序列 \(a\) ,其中 \(1\sim n\) 每个数恰好出现两次。
每次你可以在 \(a\) 的开头或末尾删除一个数,并将其加入序列 \(b\) 。
询问 \(b\) 是否可能是一个回文序列,即 \(\forall 1\le i\le n,b_i=b_{2n+1-i}\) 。
如果可以,输出字典序最小的操作序列(我们认为在开头删除字典序小于在末尾删除),否则输出 -1 。
数据范围
- \(1\le T\le 100,1\le\sum n\le 5\cdot 10^5\)。
时间限制 \(\texttt{1s}\) ,空间限制 \(\texttt{512MB}\) 。
分析
枚举第一步删了哪个数,那么最后一步删的数是固定的,此后 \(a\) 从双端队列变成两个栈。
每次从某个栈中删掉栈顶 \(x\) ,就意味着最后一步操作是删掉栈底的 \(x\) 。
将这两个 \(x\) 同时删去,再重复上面的操作即可。
为保证字典序最小,我们应该优先尝试从左边的栈中删除元素。
时间复杂度 \(\mathcal O(\sum n)\) 。
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e6+5;
int m,n,t;
int a[maxn],b[maxn];
bool work(int op)
{
deque<int> q[2];
if(!op)
{
b[1]=0,b[m]=0;
for(int i=2;a[i]!=a[1];i++) q[0].push_back(a[i]);
for(int i=m;a[i]!=a[1];i--) q[1].push_back(a[i]);
}
else
{
b[1]=1,b[m]=0;
for(int i=1;a[i]!=a[m];i++) q[0].push_back(a[i]);
for(int i=m-1;a[i]!=a[m];i--) q[1].push_back(a[i]);
}
for(int i=2,j=m-1;q[0].size()||q[1].size();)
{
int flg=0;
for(int k=0;k<=1;k++)
for(int l=0;l<=1;l++)
if(!flg&&q[0].size()>=2-k-l&&q[1].size()>=k+l&&q[k].front()==q[l].back())
flg=1,b[i++]=k,b[j--]=l,q[k].pop_front(),q[l].pop_back();
if(!flg) return false;
}
return true;
}
int main()
{
scanf("%d",&t);
while(t--)
{
scanf("%d",&n),m=2*n;
for(int i=1;i<=m;i++) scanf("%d",&a[i]);
if(work(0)||work(1))
{
for(int i=1;i<=m;i++) putchar(!b[i]?'L':'R');
putchar('\n');
}
else printf("-1\n");
}
return 0;
}
D.交通规划
题目描述
平面上有 \(n\) 条水平直线和 \(m\) 条竖直直线,因此有 \(n\times m\) 个格点。
相邻两个格点之间的线段称为边,边权为 \(w_i\) 。
每条直线两端还有一个附加点,按照上右下左的顺序依次编号 \(1\sim 2n+2m\) 。
\(T\) 次询问,每次给定 \(k\) 个附加点的颜色(黑或白)与到格点的边权,你需要将每个格点染成黑色或白色,使得两端颜色不同的边的边权和最小,输出最小值。
数据范围
- \(2\le n,m\le 500\) 。
- \(1\le T,\sum k\le 50\) ,保证单组询问附加点位置两两不同。
- \(0\le w_i\le 10^6\) 。
时间限制 \(\texttt{3s}\) ,空间限制 \(\texttt{512MB}\) 。
分析
本质是求黑白点的最小割,直接跑网络流可以获得 \(60\) 分。
再考虑 \(k=2\) 的情况。
相信大家都做过狼抓兔子,其中涉及到平面图最小割转对偶图最短路的套路。
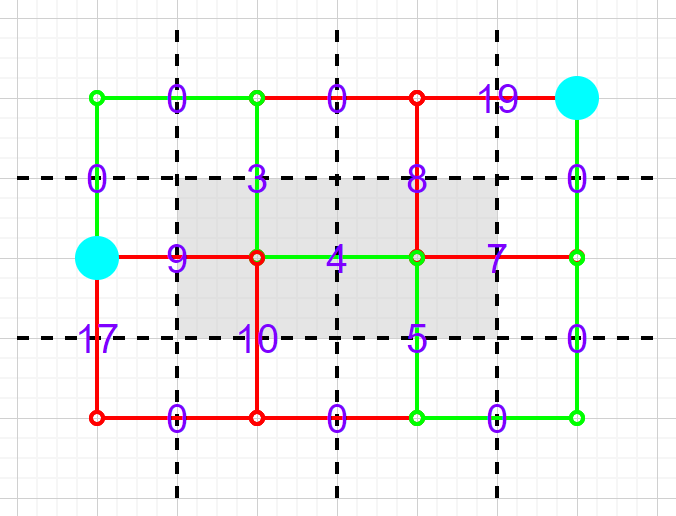
下面这张图为样例:
如果两个附加点颜色相同,显然答案为零。
否则直接跑对偶图最短路,时间复杂度 \(\mathcal O(Tnm\log(nm))\) 。
再考虑 \(k=3\) 的情况。
不妨设三个附加点为两黑一白,在环的意义下这两个黑点是相邻的。
仿照\(k=2\)的做法,我们需要从这两个黑点分别连出去一条边,但这和从一个虚点连出去两条边效果等价。
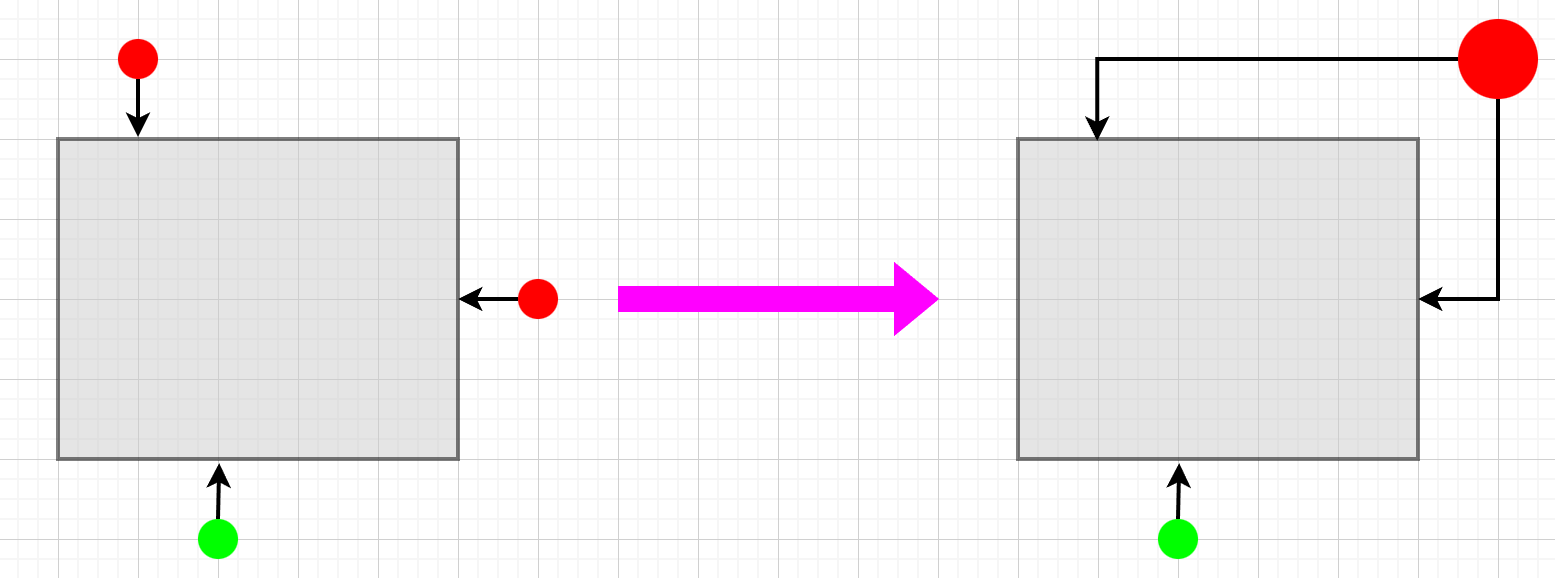
此后和 \(k=2\) 本质相同。
对于 \(k\) 更大的情况,还是先将相邻的同色点合并成一个点。
跑 \(\mathcal O(k)\) 轮单源最短路,即可求出任两个点之间的距离。
我们的想法很简单,将所有合并后的点两两配对,那么答案为每一对点的最短路距离和!
正确性证明:
回顾 \(k=2\) 的染色方案,最短路两侧分别为黑色和白色。
对于 \(k>2\) ,容易发现最优方案中最短路两两不重合(边集不交),这是因为如果出现重合的边集,可以交换配对方案使得交集的贡献从两次变成零次,距离和变小。
每次加入一对匹配,最短路和矩形边框会构成一个连通块。
翻转连通块外面所有点的颜色,连通块内部保持不变,答案增量为最短路长度。
由于路径不交,每次相当于花费最短路长度的代价,将其他所有点和这两个附加点割开,符合最小割的定义。
注意到如果环上依次存在四个点 \(a,b,c,d\) ,满足 \(a,c\) 配对、 \(b,d\) 配对,则它们的最短路一定有公共点。
交换经过公共点后面的路径,我们可以重排使得 \(a,b\) 配对、 \(c,d\) 配对,这样最短路长度之和不会变劣。
因此存在一种最优方案,使得任意两对点均不相交。
令 \(f_{l,r}\) 表示将 \([l,r]\) 中的点配对,最短路之和的最小值。转移方程为:
根据环形\(\texttt{dp}\)的套路,我们需要把数组复制一份接在原来的后面。
时间复杂度 \(\mathcal O(\sum knm\log(nm)+\sum k^3)\) 。
#include<bits/stdc++.h>
#define ll long long
#define fi first
#define se second
#define mp make_pair
#define pii pair<int,int>
using namespace std;
const int maxn=505,maxm=2.5e5+1005;
const ll inf=1e18;
int k,m,n,t,x,cnt;
int c[maxn][maxn],r[maxn][maxn],id[maxn][maxn];
int pos[maxn];
bool vis[maxm];
ll d[maxm],f[maxn][maxn],dis[maxn][maxn];
vector<pii> g[maxm];
struct node
{
int col,pos,val;
}e[maxn];
inline bool cmp(node a,node b)
{
return a.pos<b.pos;
}
inline void addedge(int u,int v,int w)
{
g[u].push_back(mp(v,w)),g[v].push_back(mp(u,w));
}
inline void dijkstra(int s)
{
priority_queue<pii,vector<pii>,greater<pii>> q;
for(int i=1;i<=cnt;i++) d[i]=inf,vis[i]=false;
d[s]=0,q.push(mp(d[s],s));
while(!q.empty())
{
int u=q.top().se;
q.pop();
if(vis[u]) continue;
vis[u]=true;
for(auto p:g[u])
{
int v=p.fi,w=p.se;
if(d[v]>d[u]+w) d[v]=d[u]+w,q.push(mp(d[v],v));
}
}
}
inline void chmin(ll &x,ll y)
{
if(x>=y) x=y;
}
signed main()
{
scanf("%d%d%d",&n,&m,&t);
for(int i=1;i<n;i++) for(int j=1;j<=m;j++) scanf("%d",&r[i][j]);
for(int i=1;i<=n;i++) for(int j=1;j<m;j++) scanf("%d",&c[i][j]);
for(int i=0;i<=n;i++) for(int j=0;j<=m;j++) id[i][j]=++cnt;
while(t--)
{
scanf("%d",&k),x=0;
for(int j=0;j<=m;j++) r[0][j]=r[n][j]=0;
for(int i=0;i<=n;i++) c[i][0]=c[i][m]=0;
for(int i=1;i<=k;i++)
{
scanf("%d%d%d",&e[i].val,&e[i].pos,&e[i].col);
int p=e[i].pos,v=e[i].val;
if(p<=m) r[0][p]=v;
else if(p<=n+m) c[p-m][m]=v;
else if(p<=n+2*m) r[n][n+2*m+1-p]=v;
else c[2*n+2*m+1-p][0]=v;
}
sort(e+1,e+k+1,cmp);
for(int i=1;i<=k;i++)
{///每个连续段,对偶图顶点由原图连续段最后一个点转化得到
if(e[i].col==e[i%k+1].col) continue;
int p=e[i].pos,r,c;
if(p<=m) r=0,c=p;
else if(p<=n+m) r=p-m,c=m;
else if(p<=n+2*m) r=n,c=n+2*m-p;
else r=2*n+2*m-p,c=0;
pos[++x]=id[r][c];
}
if(!x)
{
printf("0\n");
continue;
}
for(int i=1;i<=cnt;i++) g[i].clear();
for(int i=0;i<=n;i++)
for(int j=0;j<=m;j++)
{
if(j) addedge(id[i][j-1],id[i][j],r[i][j]);
if(i) addedge(id[i-1][j],id[i][j],c[i][j]);
}
for(int i=1;i<=x;i++)
{
dijkstra(pos[i]);
for(int j=1;j<=x;j++) dis[i][j]=d[pos[j]];
}
ll res=inf;
for(int len=2;len<=x;len+=2)
for(int l=1,r=len;r<=2*x;l++,r++)
{
f[l][r]=dis[(l-1)%x+1][(r-1)%x+1]+f[l+1][r-1];
for(int i=l+1;i<r;i+=2) chmin(f[l][r],f[l][i]+f[i+1][r]);
if(len==x) chmin(res,f[l][r]);
}
printf("%lld\n",res);
}
return 0;
}
本文来自博客园,作者:peiwenjun,转载请注明原文链接:https://www.cnblogs.com/peiwenjun/p/17312462.html


 浙公网安备 33010602011771号
浙公网安备 33010602011771号