作业总结

前言：

随着学习的不断深入，作业的难度也逐渐提升，自己对于平面直角坐标系的相关计算的熟练程度还是不高，对于期中考试的Arraylist类也不是很熟，仍要努力。

设计与分析：

pta上图形设计类题目一直都挺难的，题目要求也很多，这道题和上次的题目有点相似，但是复杂程度又上了一个台阶。题目要求如下：

 

• 用户输入一组选项和数据，进行与四边形有关的计算。
• 以下四边形顶点的坐标要求按顺序依次输入，连续输入的两个顶点是相邻顶点，第一个和最后一个输入的顶点相邻。
• 选项包括：
• 1：输入四个点坐标，判断是否是四边形、平行四边形，判断结果输出true/false，结果之间以一个英文空格符分隔。
• 2：输入四个点坐标，判断是否是菱形、矩形、正方形，判断结果输出true/false，结果之间以一个英文空格符分隔。 若四个点坐标无法构成四边形，输出"not a quadrilateral"
• 3：输入四个点坐标，判断是凹四边形（false）还是凸四边形(true)，输出四边形周长、面积，结果之间以一个英文空格符分隔。 若四个点坐标无法构成四边形，输出"not a quadrilateral"
• 4：输入六个点坐标，前两个点构成一条直线，后四个点构成一个四边形或三角形，输出直线与四边形（也可能是三角形）相交的交点数量。如果交点有两个，再按面积从小到大输出四边形(或三角形)被直线分割成两部分的面积（不换行）。若直线与四边形或三角形的一条边线重合，输出"The line is coincide with one of the lines"。若后四个点不符合四边形或三角形的输入，输出"not a quadrilateral or triangle"。
• 后四个点构成三角形的情况：假设三角形一条边上两个端点分别是x、y，边线中间有一点z，另一顶点s：
• 1）符合要求的输入：顶点重复或者z与xy都相邻，如x x y s、x z y s、x y x s、s x y y。此时去除冗余点，保留一个x、一个y。
• 2) 不符合要求的输入：z 不与xy都相邻，如z x y s、x z s y、x s z y
• 5：输入五个点坐标，输出第一个是否在后四个点所构成的四边形（限定为凸四边形，不考虑凹四边形）或三角形（判定方法见选项4）的内部（若是四边形输出in the quadrilateral/outof the quadrilateral，若是三角形输出in the triangle/outof the triangle）。如果点在多边形的某条边上，输出"on the triangle或者on the quadrilateral"。若后四个点不符合四边形或三角形，输出"not a quadrilateral or triangle"。

• 输入格式:

• 基本格式：选项+":"+坐标x+","+坐标y+" "+坐标x+","+坐标y。点的x、y坐标之间以英文","分隔，点与点之间以一个英文空格分隔。

• 输出格式:

• 基本输出格式见每种选项的描述。
• 异常情况输出：
• 如果不符合基本格式，输出"Wrong Format"。
• 如果符合基本格式，但输入点的数量不符合要求，输出"wrong number of points"。
• 注意：输出的数据若小数点后超过3位，只保留小数点后3位，多余部分采用四舍五入规则进到最低位。小数点后若不足3位，按原始位数显示，不必补齐。例如：1/3的结果按格式输出为 0.333，1.0按格式输出为1.0
• 选项1、2、3中，若四边形四个点中有重合点，输出"points coincide"。
• 选项4中，若前两个输入线的点重合，输出"points coincide"。

 

这次我从第一个要求开始就感觉无从下手了，百度了一下以后才稍微有了一点思路，判定四边形只要看是否有三个点连成直线即可，如果给出的四个点中有三个点在同一条直线上那就不是四边形了，代码如下：

class SBX
    {
        public int Px1, Px2, Px3, Px4, Py1, Py2, Py3, Py4;  //顶点坐标
        public boolean IsSBX()                                 //判断是否是四边形
        {
            if ((Py4 - Py3) * (Px4 - Px2) == (Py4 - Py2) * (Px4 - Px3))
                return false;
            else if ((Py4 - Py3) * (Px4 - Px1) == (Py4 - Py1) * (Px4 - Px3))
                return false;
            else if ((Py4 - Py2) * (Px4 - Px1) == (Py4 - Py1) * (Px4 - Px2))
                return false;
            else if ((Py3 - Py2) * (Px3 - Px1) == (Py3 - Py1) * (Px3 - Px2))
                return false;                               //任意三个顶点成直线，非四边形
            else
                return true;
        }

然后判断是否为平行四边形只需要在是四边形的前提下判断两组对边是否分别平行(即边的斜率相等）即可，通过代码实现如下：

class PXSBX extends SBX                                       //平行四边形类，继承四边形类                   
    {
        public boolean IsPXSBX()                               //判断是否为平行四边形
        {
            if (((Py2 - Py1) * (Px4 - Px3) == (Py4 - Py3) * (Px2 - Px1)) && ((Py4 - Py1) * (Px2 - Px3) == (Py2 - Py3) * (Px4 - Px1)))
                return true;
            else if (((Py3 - Py1) * (Px4 - Px2) == (Py4 - Py2) * (Px3 - Px1)) && ((Py4 - Py1) * (Px2 - Px3) == (Py2 - Py3) * (Px4 - Px1)))
                return true;
            else if (((Py2 - Py1) * (Px4 - Px3) == (Py4 - Py3) * (Px2 - Px1)) && ((Py3 - Py1) * (Px2 - Px4) == (Py2 - Py4) * (Px3 - Px1)))
                return true;                                //两组对边分别平行（即边的斜率相等）的四边形则为平行四边形
            else
                return false;                                          
        }
    }

对于第二个要求，只要先判断四边形是否是平行四边形，如果不是，那肯定不是矩形、菱形或者正方形其中之一，如果是接下来再判断是否是矩形，若为四边相等的平行四边形则为菱形，若为四边相等的矩形则为正方形，通过代码实现如下：

class JX extends PXSBX
    {
        public boolean IsJX()                                  //判断是否为矩形
        {
            double I1, I2, I3;                              //某个顶点分别到其他三个顶点的距离的平方
            I1= Math.Abs((Px1 - Px2) * (Px1 - Px2) + (Py1 - Py2) * (Py1 - Py2));
            I2= Math.Abs((Px1 - Px3) * (Px1 - Px3) + (Py1 - Py3) * (Py1 - Py3));
            I3= Math.Abs((Px1 - Px4) * (Px1 - Px4) + (Py1 - Py4) * (Py1 - Py4));
            if (I1 > I2 && I1 > I3 && (I2 + I3 == I1))
                return true;
            else if (I2 > I1 && I2 > I3 && (I1 + I3 == I2))
                return true;
            else if (I3 > I1 && I3 > I2 && (I1 + I2 == I3))
                return true;                               //勾股定理，及有一个直角的平行四边形为矩形
            else
                return false; 
        }
    }

第三个要求坦白说我对于判断四边形的凹凸性毫无经验， 只能再次百度，其中的数学原理是：按照输入顺序依次将点连接起来，对于连续的三个点p0,p1,p2，另向量a=p1-p0，b=p2-p1，若是凸多边形，那么b相对于a一定是向逆时针方向旋转的，判断两向量的旋转方向，可以使用向量的叉积 a×b ＝ x1×y2 － x2×y1，分为三种情况：

a×b > 0 b在a的逆时针方向

a×b = 0 b平行于a（共线）

a×b < 0 b在a的顺时针方向

代码如下：

t1 = (p4.x-p1.x)(p2.y-p1.y)-(p4.y-p1.y)(p2.x-p1.x);
t2 = (p1.x-p2.x)(p3.y-p2.y)-(p1.y-p2.y)(p3.x-p2.x);
t3 = (p2.x-p3.x)(p4.y-p3.y)-(p2.y-p3.y)(p4.x-p3.x);
t4 = (p3.x-p4.x)(p1.y-p4.y)-(p3.y-p4.y)(p1.x-p4.x);
if (t1*t2*t3*t4 < 0)
　return Concavequadrilateral;//（凹四边形）
if (t1*t2*t3*t4 < 0)
　return Convexquadrilateral;//（凸四边形）

对于第四和第五个要求则难度加倍了，对于第四个要求判断形状和第一题类似，但是求分割的面积则要依据后四个点构成图形的形状有所不同，如果是三角形就容易一点，因为如果直线将三角形分为两个图形的话其中必有一个是三角形，我们只要求出这个小三角形的面积，然后用大三角形的面积减去小三角形的面积即可；但是如果后四个点构成的是四边形的话要麻烦的多，因为直线与四边形相交有可能将四边形分割为一个四边形一个三角形或者两个三角形或者两个四边形，判断的难度很大。第五个要求判断的方法要用到第三个要求中的矢量叉乘法，

计算矢量叉积是与直线和线段相关算法的核心部分。设矢量P = ( x1, y1 )，Q = ( x2, y2 )，则矢量叉积定义为由(0,0)、p1、p2和p1+p2所组成的平行四边形的带符号的面积，即：P × Q = x1*y2 - x2*y1，其结果是一个标量。显然有性质 P × Q = - ( Q × P ) 和 P × ( - Q ) = - ( P × Q )。一般在不加说明的情况下，本文下述算法中所有的点都看作矢量，两点的加减法就是矢量相加减，而点的乘法则看作矢量叉积。叉积的一个非常重要性质是可以通过它的符号判断两矢量相互之间的顺逆时针关系：

 

　　若 P × Q > 0 , 则P在Q的顺时针方向。

 

　　若 P × Q < 0 , 则P在Q的逆时针方向。

 

　　若 P × Q = 0 , 则P与Q共线，但可能同向也可能反向。

所以，假设该凸四边形为ABCD，且ABCD顺时针，待判断的点为M，则需要满足：

 

      AB × AM>0

 

      BC × BM>0

 

      CD × CM>0

 

      DA × DM>0

即可证明点M在凸四边形内部。

接下来的期中考试题目难度也是逐级递增的，后面的题只要改一改前面的代码就可以用了，而且这次期中考试也考察了我们对于类图的熟悉程度和将类图转化为代码的能力，题目要求如下：

• 设计一个类表示平面直角坐标系上的点Point，私有属性分别为横坐标x与纵坐标y，数据类型均为实型数，除构造方法以及属性的getter与setter方法外，定义一个用于显示信息的方法display(),用来输出该坐标点的坐标信息，格式如下：(x,y)，数值保留两位小数。为简化题目，其中，坐标点的取值范围设定为(0,200]。若输入有误，系统则直接输出Wrong Format

• 设计一个类表示平面直角坐标系上的线Line，私有属性除了标识线段两端的点point1、point2外，还有一个字符串类型的color，用于表示该线段的颜色，同样，除构造方法以及属性的getter与setter方法外，定义一个用于计算该线段长度的方法getDistance(),还有一个用于显示信息的方法display(),用来输出线段的相关信息

 

 

 

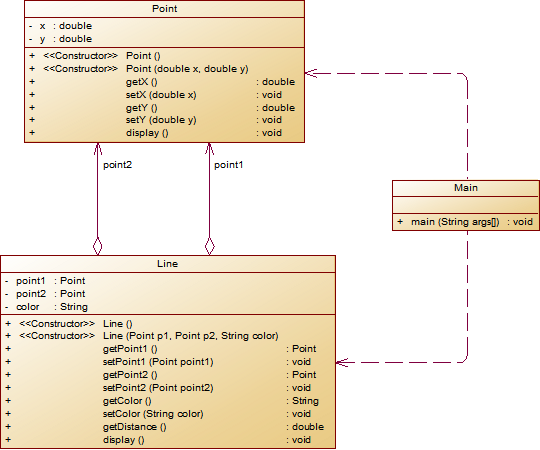
 我的代码如下：

import java.util.Scanner;
public class Main {
    public static void main(String[] args){
       Scanner sc = new Scanner(System.in);
       Line l = new Line();
       double a[] = new double[4];
       for(int i = 0;i < a.length;i ++) {
           a[i] = sc.nextDouble();
           if(a[i] > 200 || a[i] <= 0) {
               System.out.println("Wrong Format");
               return;
           }
       }
           Point p1 = new Point();
           p1.setX(a[0]);
           p1.setY(a[1]);
           Point p2 = new Point();
           p2.setX(a[2]);
           p2.setY(a[3]);
           l.setColor(sc.next());
           l.setPoint1(p1);
           l.setPoint2(p2);
           l.display();
    }
}
class Point{
    private double x;
    private double y;
    public Point(){
        
    }
    public Point(double x,double y){
        x = getX();
        y = getY();
    }
    public void display() {
        System.out.printf("(%.2f,%.2f)",x,y);
    }
    public double getY() {
        return y;
    }
    public void setY(double y) {
        this.y = y;
    }
    public double getX() {
        return x;
    }
    public void setX(double x) {
        this.x = x;
    }
    
}
class Line{
    private Point point1,point2;
    private String color;
    public Line() {
        
    }
    public Line(Point p1,Point p2,String color) {
        point1 = p1;
        point2 = p2;
        this.color = color;
    }
    public Point getPoint1() {
        return point1;
    }
    public void setPoint1(Point point1) {
        this.point1 = point1;
    }
    public Point getPoint2() {
        return point2;
    }
    public void setPoint2(Point point2) {
        this.point2 = point2;
    }
    public String getColor() {
        return color;
    }
    public void setColor(String color) {
        this.color = color;
    }
    public double getDistance() {
        return Math.sqrt(Math.pow(point1.getX()-point2.getX(), 2) + Math.pow(point1.getY()-point2.getY(),2));
    }
    public void display() {
        System.out.println("The line's color is:" + getColor());
        System.out.println("The line's begin point's Coordinate is:");
        System.out.printf("(%.2f,%.2f)\n",point1.getX(),point1.getY());
        System.out.println("The line's end point's Coordinate is:");
        System.out.printf("(%.2f,%.2f)\n",point2.getX(),point2.getY());
        System.out.printf("The line's length is:%.2f" ,getDistance());
    }
}

看起来挺容易的题目，只要照着类图将所有的方法写出来，然后在适当的地方调用即可。

第二题要求如下：

在“点与线（类设计）”题目基础上，对题目的类设计进行重构，以实现继承与多态的技术性需求。

• 对题目中的点Point类和线Line类进行进一步抽象，定义一个两个类的共同父类Element（抽象类），将display()方法在该方法中进行声明（抽象方法），将Point类和Line类作为该类的子类。
• 再定义一个Element类的子类面Plane，该类只有一个私有属性颜色color，除了构造方法和属性的getter、setter方法外，display()方法用于输出面的颜色，输出格式如下：The Plane's color is:颜色
• 在主方法内，定义两个Point（线段的起点和终点）对象、一个Line对象和一个Plane对象，依次从键盘输入两个Point对象的起点、终点坐标和颜色值（Line对象和Plane对象颜色相同），然后定义一个Element类的引用，分别使用该引用调用以上四个对象的display()方法，从而实现多态特性。

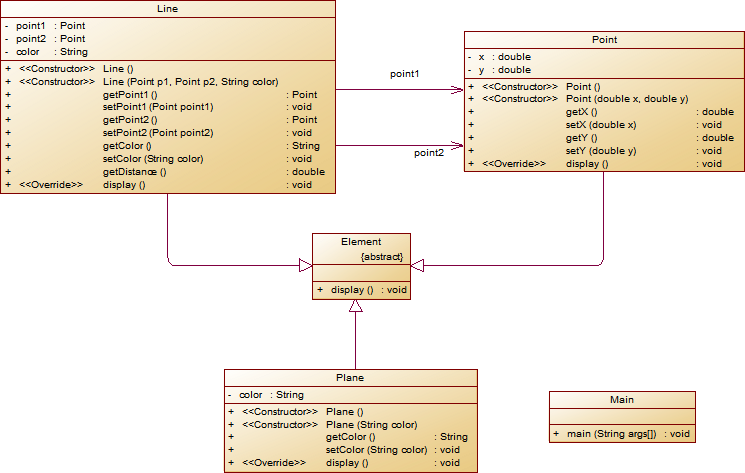
这道题考察了我们对继承和多态的熟悉程度，还有一个接口，也挺容易的。

import java.util.Scanner;
public class Main {
    public static void main(String[] args){
       Scanner sc = new Scanner(System.in);
       Line l = new Line();
       Plane pl = new Plane();
       double a[] = new double[4];
       for(int i = 0;i < a.length;i ++) {
           a[i] = sc.nextDouble();
           if(a[i] > 200 || a[i] <= 0) {
               System.out.println("Wrong Format");
               return;
           }
       }
           Point p1 = new Point();
           p1.setX(a[0]);
           p1.setY(a[1]);
           Point p2 = new Point();
           p2.setX(a[2]);
           p2.setY(a[3]);
           l.setColor(sc.next());
           pl.setColor(l.getColor());
           l.setPoint1(p1);
           l.setPoint2(p2);
           l.display();
    }
}
abstract class Element{
    public abstract void display();
}
class Plane extends Element{
    private String color;
    Plane(){
        
    }
    Plane(String color){
        
    }
    public String getColor() {
        return color;
    }

    public void setColor(String color) {
        this.color = color;
    }

    public void display() {
        System.out.println("The Plane's color is:" + getColor());
    }
    
}
class Point extends Element{
    private double x;
    private double y;
    public Point(){
        
    }
    public Point(double x,double y){
        x = getX();
        y = getY();
    }
    public void display() {
        System.out.printf("(%.2f,%.2f)",x,y);
    }
    public double getY() {
        return y;
    }
    public void setY(double y) {
        this.y = y;
    }
    public double getX() {
        return x;
    }
    public void setX(double x) {
        this.x = x;
    }
    
}
class Line extends Element{
    private Point point1,point2;
    private String color;
    public Line() {
        
    }
    public Line(Point p1,Point p2,String color) {
        point1 = p1;
        point2 = p2;
        this.color = color;
    }
    public Point getPoint1() {
        return point1;
    }
    public void setPoint1(Point point1) {
        this.point1 = point1;
    }
    public Point getPoint2() {
        return point2;
    }
    public void setPoint2(Point point2) {
        this.point2 = point2;
    }
    public String getColor() {
        return color;
    }
    public void setColor(String color) {
        this.color = color;
    }
    public double getDistance() {
        return Math.sqrt(Math.pow(point1.getX()-point2.getX(), 2) + Math.pow(point1.getY()-point2.getY(),2));
    }
    public void display() {
        System.out.printf("(%.2f,%.2f)\n",point1.getX(),point1.getY());
        System.out.printf("(%.2f,%.2f)\n",point2.getX(),point2.getY());
        System.out.println("The line's color is:" + getColor());
        System.out.println("The line's begin point's Coordinate is:");
        System.out.printf("(%.2f,%.2f)\n",point1.getX(),point1.getY());
        System.out.println("The line's end point's Coordinate is:");
        System.out.printf("(%.2f,%.2f)\n",point2.getX(),point2.getY());
        System.out.printf("The line's length is:%.2f\n" ,getDistance());
        System.out.println("The Plane's color is:" + getColor());
    }
}

第三题则增加了一个容器类，考察我们对ArrayList类的熟悉程度已及能否熟练运用，ArrayList 类是一个可以动态修改的数组，与普通数组的区别就是它是没有固定大小的限制，我们可以添加或删除元素。ArrayList 继承了 AbstractList ，并实现了 List 接口。在这题中我们需要运用ArrayList类自带的一些方法来帮助我们解题，比如add（）和remove（）方法在这题就有出场，题目要求如下：

在“点与线（继承与多态）”题目基础上，对题目的类设计进行重构，增加容器类保存点、线、面对象，并对该容器进行相应增、删、遍历操作。

• 在原有类设计的基础上，增加一个GeometryObject容器类，其属性为ArrayList<Element>类型的对象（若不了解泛型，可以不使用<Element>）
• 增加该类的add()方法及remove(int index)方法，其功能分别为向容器中增加对象及删除第index - 1（ArrayList中index>=0）个对象
• 在主方法中，用户循环输入要进行的操作（choice∈[0,4]），其含义如下：
  • 1：向容器中增加Point对象
  • 2：向容器中增加Line对象
  • 3：向容器中增加Plane对象
  • 4：删除容器中第index - 1个数据，若index数据非法，则无视此操作
  • 0：输入结束

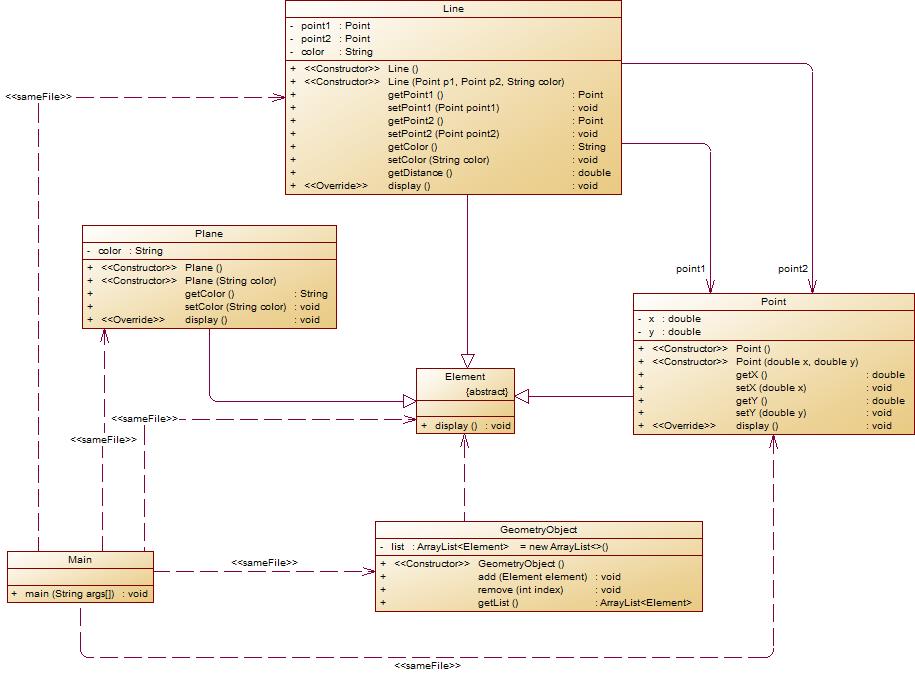
可以看出来类图也更加复杂了，说实话我对ArrayList类并不熟悉所以这题没有拿到满分。

import java.util.Scanner;
import java.util.ArrayList;

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        GeometryObject g= new GeometryObject();
        int choice = sc.nextInt();
        double a[] = new double[4];
        while (choice != 0) {
            switch (choice) {
            case 1:// insert Point object into list
                
                for (int i = 0; i < 2; i++) {
                    a[i] = sc.nextDouble();
                    if (a[i] > 200 || a[i] <= 0) {
                        System.out.println("Wrong Format");
                        return;
                    }
                }
                Point p1 = new Point();
                g.add(p1);
                break;
            case 2:// insert Line object into list
                Line l = new Line();
                for (int i = 0; i < 4; i++) {
                    a[i] = sc.nextDouble();
                    if (a[i] > 200 || a[i] <= 0) {
                        System.out.println("Wrong Format");
                        return;
                    }
                }
                Point p11 = new Point();
                p11.setX(a[0]);
                p11.setY(a[1]);
                Point p21 = new Point();
                p21.setX(a[2]);
                p21.setY(a[3]);
                l.setColor(sc.next());
//                l.setPoint1(p11);
//                l.setPoint2(p21);
//                l.display();
                g.add(l);
                break;
            case 3:// insert Plane object into list
                Plane pl = new Plane();
                pl.setColor(sc.next());
                g.add(pl);
                break;
            case 4:// delete index - 1 object from list
                int index = sc.nextInt();
                g.remove(index);
            case 0:
                break;
            }
            choice = sc.nextInt();
        }
    }
}

abstract class Element {
    public abstract void display();
}

class Plane extends Element {
    private String color;

    Plane() {

    }

    Plane(String color) {

    }

    public String getColor() {
        return color;
    }

    public void setColor(String color) {
        this.color = color;
    }

    public void display() {
        System.out.println("The Plane's color is:" + getColor());
    }

}

class Point extends Element {
    private double x;
    private double y;

    public Point() {

    }

    public Point(double x, double y) {
        x = getX();
        y = getY();
    }

    public void display() {
        System.out.printf("(%.2f,%.2f)", x, y);
    }

    public double getY() {
        return y;
    }

    public void setY(double y) {
        this.y = y;
    }

    public double getX() {
        return x;
    }

    public void setX(double x) {
        this.x = x;
    }

}

class Line extends Element {
    private Point point1, point2;
    private String color;

    public Line() {

    }

    public Line(Point p1, Point p2, String color) {
        point1 = p1;
        point2 = p2;
        this.color = color;
    }

    public Point getPoint1() {
        return point1;
    }

    public void setPoint1(Point point1) {
        this.point1 = point1;
    }

    public Point getPoint2() {
        return point2;
    }

    public void setPoint2(Point point2) {
        this.point2 = point2;
    }

    public String getColor() {
        return color;
    }

    public void setColor(String color) {
        this.color = color;
    }

    public double getDistance() {
        return Math.sqrt(Math.pow(point1.getX() - point2.getX(), 2) + Math.pow(point1.getY() - point2.getY(), 2));
    }

    public void display() {
        System.out.printf("(%.2f,%.2f)\n", point1.getX(), point1.getY());
        System.out.printf("(%.2f,%.2f)\n", point2.getX(), point2.getY());
        System.out.println("The line's color is:" + getColor());
        System.out.println("The line's begin point's Coordinate is:");
        System.out.printf("(%.2f,%.2f)\n", point1.getX(), point1.getY());
        System.out.println("The line's end point's Coordinate is:");
        System.out.printf("(%.2f,%.2f)\n", point2.getX(), point2.getY());
        System.out.printf("The line's length is:%.2f\n", getDistance());
        System.out.println("The Plane's color is:" + getColor());
    }
}

class GeometryObject {
    private ArrayList<Element> list = new ArrayList<>();

    public GeometryObject() {
        // TODO Auto-generated constructor stub
    }

    public void add(Element element) {
        list.add(element);
    }

    public void remove(int index) {
        if(index < 0) {
            
        }else {
            list.remove(index - 1);
        }
    }

    public ArrayList<Element> getList() {
        for(int i=0;i<list.size();i++) {
            list.get(i).display();
        }
        return list;
    }
}

 心得体会：

通过这几次作业，我自认为收获了很多，在写题之前要弄清楚题目要求，在心中有个大致的框架，比如要写哪些函数，我要怎么做才能满足这个要求，这么做会不会太麻烦了，有没有什么更好的解决方法等等，万万不可想到哪写到哪，我在写题过程中查阅了许多资料，我也将在接下来的学习过程中不断充实自己的知识体系，虽然现在仍然不擅长写平面直角坐标系下的计算题，但我不会退缩，下次也会争取写出来。我还会不断学习，争取掌握ArrayList类的使用方法！

改进建议：

对于老师布置的作业，我觉得在pta的作业截止以后最好能给我们一份正确的代码，让我们学习一下解题思路和解题技巧，也能让我们发现自己的不足，对于我自身，我也会在课余时间多花些时间在复习和预习上面，老师讲过了ArrayList类，但是因为我并没有好好复习导致没有取得满意的分数，这点让我很自责，我将花更多时间用在练习上，不断提高自己的能力。