19. 删除链表的倒数第 N 个结点142.环形链表Ⅱ

19. 删除链表的倒数第 N 个结点

题目链接 删除链表的倒数第N个结点

题目描述

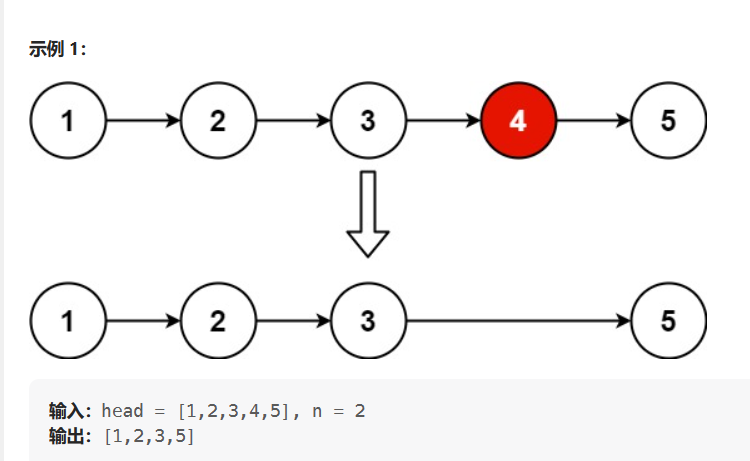
给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

思路

第一次看到这道题，想到两种方法

• 获取链表的长度然后凭size-n可获取删除结点的前驱，之后便可以删除元素
• 也可以通过反转链表之后再获取第n个结点

双指针法：利用快慢指针进行遍历。如果快指针先移动n步，之后快慢指针一起移动，当快指针移动到链表结尾的null结点时，慢指针移动到删除结点的位置。由于慢指针应该要移动到删除结点的前驱位置，才可以对下一个结点进行删除，故我们可以这样做

• 一开始，快指针移动n+1步；
• 快慢指针同时移动；
• 当快指针指向null时，慢指针指向了删除结点的前驱；
• 删除结点；

代码

1.常规思路

点击查看代码

class Solution {
    /**
     * 移除倒数第n个结点
     * @param head
     * @param n
     * @return
     */
    public ListNode removeNthFromEnd(ListNode head, int n) {
        //获取链表长度，将cur移动到删除元素的前驱，删除元素
        //倒数第n个的有效性
        if(n<0) return head;
        ListNode dummy = new ListNode(0,head);
        ListNode cur = dummy;
        int size = 0;
        //获取链表长度
        while(cur.next!=null){
            cur = cur.next;
            size++;
        }
        //倒数第n个的有效性
        if(n>size) return head;
        cur = dummy;
        //将cur移动到删除元素的前驱
        for (int i = 1; i <= size-n ; i++) {
            cur = cur.next;
        }
        //删除元素
        cur.next = cur.next.next;
		//返回头结点
        return dummy.next;
    }
}

2.双指针法

点击查看代码

class Solution {
    /**
     * 移除倒数第n个结点
     * @param head
     * @param n
     * @return
     */
    public ListNode removeNthFromEnd(ListNode head, int n) {
        //判断n的有效性
        if(n<0) return head;
        //设置虚拟头结点
        ListNode dummy = new ListNode(0,head);
        //定义快慢指针
        ListNode fast = dummy;
        ListNode slow = dummy;
        //fast指针先移动n+1步
        for (int i = 0; i < n + 1; i++) {
            fast = fast.next;
        }
        //通过fast控制slow指针指向删除结点的前驱
        while(fast!=null){
            fast = fast.next;
            slow = slow.next;
        }
        //删除元素
        slow.next = slow.next.next;
		//返回头结点
        return dummy.next;
    }
}

总结

1.这道题是双指针法的经典应用，需要熟练掌握；
2.使用双指针法如果有些步骤不清楚的话，可以静下心去想指针移动的过程。

142.环形链表Ⅱ

题目链接 环形链表Ⅱ

题目描述

给定一个链表的头节点 head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。
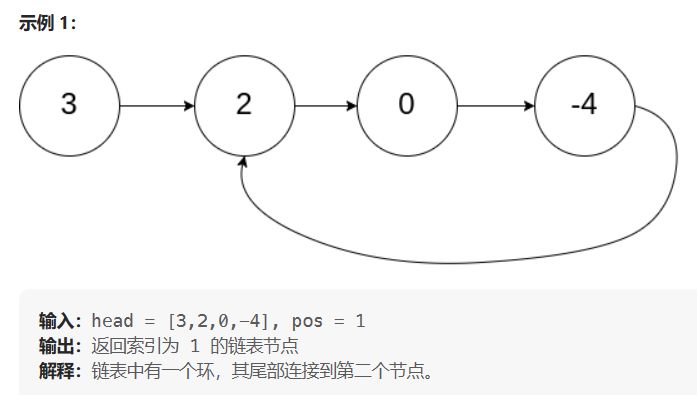
如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。不允许修改链表。

思路

• 如何判断链表是否有环
• 如果有环，如何找到环的入口

如何判断链表是否有环

使用双指针法：快指针走两步，慢指针走1步，如果快慢指针相遇则证明有环

如果有环，如何找到环的入口

如图所示：(x代表头节点到环形入口节点的节点数;y代表环形入口节点到相遇节点的节点数;z代表相遇节点到环形入口节点的节点数;n表示fast经过环的圈数>=1)

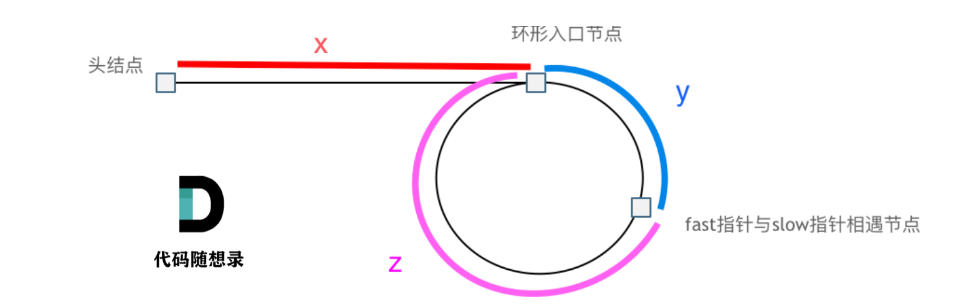
满足:

• slow经过的节点数=x+y,fast经过的节点数=x+y+n(y+z)
• 由于fast的经过节点数是slow的两倍，则存在2（x+y）=x+y+n(y+z)
• 化简得 x=n(y+z)-y-->x = (n-1)(y+z)+z
• 以上式子意味着：
  n=1时，x=z,即fast转了一圈后在某处与slow相遇，此时有x=z，则可以设置两个指针index1,index2分别指向相遇节点和头节点，同时移动，直到指针相遇在环形入口节点，获得该节点。
  n>1时，fast转了n圈后与slow相遇，相遇时有x=n(y+z)+z,index1 指针在环里多转了(n-1)圈，然后再遇到index2，相遇点依然是环形的入口节点。

双指针法中存在的疑问：

1.在环中，fast指针和slow指针为什么一定会相遇呢？
因为fast是走两步，slow是走一步，其实相对于slow来说，fast是一个节点一个节点的靠近slow的，所以fast一定可以和slow重合。
2.慢指针在走完一圈前一定会和快指针相遇？
假设极端情况：慢指针（假设位置为[0]）刚进入环时，就在快指针[1]的后面，快指针走了一圈,长度为len,到达原来的位置[1],同时慢指针走了半圈，长度为len/2,位置为[len/2],之后快指针再走一圈，长度同样为len，到达原来的位置[1],同时慢指针再走了半圈，长度同样为len/2,此时的位置为[0],很显然，快指针走了2圈的时候，慢指针走了一圈，且快指针此时已经越过慢指针[0]到达[1]的位置。可得：慢指针在走完一圈前就已经被超过了。
3.为什么n>=1 ？
慢指针进入环时，快指针已经在环中，快指针去追慢指针必然走完一圈及以上

代码

点击查看代码

public class Solution {
    public ListNode detectCycle(ListNode head) {
		//设置快慢指针
        ListNode slow = head;
        ListNode fast = head;
        while (fast!=null&&fast.next!=null){
		//fast走两步,slow走1步
        fast = fast.next.next;
        slow = slow.next;
        if(fast==slow){//指针相遇
             ListNode index1 = fast;
             ListNode index2 = head;
             while(index1!=index2){//指针未相遇
             		index1 = index1.next;
                    index2 = index2.next;
                 }
		 //跳出循环则获得环形入口节点
         	return index1;
            }
        }
        return null;
    }
}