977.有序数组的平方008.长度最小的子数组

977.有序数组的平方

【题目链接】有序数组的平方

【题目描述】

给你一个按 非递减顺序 排序的整数数组 nums，返回 每个数字的平方 组成的新数组，要求也按 非递减顺序 排序。

输入：nums = [-4,-1,0,3,10]
输出：[0,1,9,16,100]
解释：平方后，数组变为 [16,1,0,9,100]
排序后，数组变为 [0,1,9,16,100]

请你设计时间复杂度为 O(n) 的算法解决本问题

【思路】

1.快速排序法
时间复杂度O(nlogn)
2.双指针法：
新数组元素的最大值只会出现在数组的两边，在数组的左右两边设置左右指针，指针对应的元素大的则放入新数组中，并且新数组是从右向左存放元素(即从下标较高的开始存放元素)
时间复杂度O(n)

【代码】

快速排序法

点击查看代码

class Solution {
    public int[] sortedSquares(int[] nums) {
        for(int i=0;i<nums.length;i++){
            nums[i] *= nums[i]; 
        }
        int left = 0;
        int right = nums.length-1;
        QuickSort(nums,left,right);
        return nums;
    }
    static void QuickSort(int nums[],int left,int right){
        int p;
        if(left<right){
            p = Partion(nums, left, right);
            QuickSort(nums,left,p-1);//比基准元素小的部分继续调用快速排序
            QuickSort(nums,p+1,right);//比基准元素大的部分继续调用快速排序
        }
    }
    static int Partion(int[] nums,int left,int right) {
        int a = nums[left];
        while(left<right) {
            while(nums[right]>=a&&left<right) {
                right--;
            }
            if(nums[right]<a){
                nums[left] = nums[right];
            }
            while(nums[left]<=a&&left<right){
                left++;
            }
            if(nums[left]>a){
                nums[right]=nums[left];
            }
        }
        nums[left] = a;
       return left;
    }

}

双指针法
1.第一种写法

点击查看代码

class Solution {
    public int[] sortedSquares(int[] nums) {
        int newnums[] = new int[nums.length];
        for (int i = 0; i < nums.length; i++) {
            nums[i] = nums[i]*nums[i];
        }
        int k = nums.length-1;
        int left = 0;
        int right = k;
        for(int i=k;i>=0;i--){
            if(nums[left]>=nums[right]){
                newnums[i] = nums[left];
                left++;
            }else{
                newnums[i] = nums[right];
                right--;
            }
        }
        return newnums;
    }
}

特征：用新数组的下标>=0控制循环结束

2.第二种写法

点击查看代码

class Solution {
    public static int[] sortedSquares(int[] nums) {
        int right = nums.length - 1;
        int left = 0;
        int[] result = new int[nums.length];
        int index = result.length - 1;
        while (left <= right) {
            if (nums[left] * nums[left] > nums[right] * nums[right]) {
                // 正数的相对位置是不变的， 需要调整的是负数平方后的相对位置
                result[index--] = nums[left] * nums[left];
                ++left;
            } else {
                result[index--] = nums[right] * nums[right];
                --right;
            }
        }
        return result;
    }
}

特征：用left<=right控制循环结束

008.长度最小的子数组

题目链接： 长度最小的子数组

题目描述

给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。

思路

注意这里是连续子数组，即原数组中连续的元素之和大于等于target，这些元素组成子数组。
暴力解法：是一个for循环滑动窗口的起始位置，一个for循环为滑动窗口的终止位置，用两个for循环 完成了一个不断搜索区间的过程。

滑动窗口：用一个for循环表示滑动窗口的终止位置，移动终止位置直到(包含起始位置到终止位置的)窗口中元素和大于等于target,就获取子序列的长度，缩小窗口(原始的窗口元素和减去起始位置的元素即sum-nums[起始位置])，向后移动起始位置(起始位置++)。只要窗口中的元素和一直大于等于target，就不断移动起始位置。否则移动终止位置。

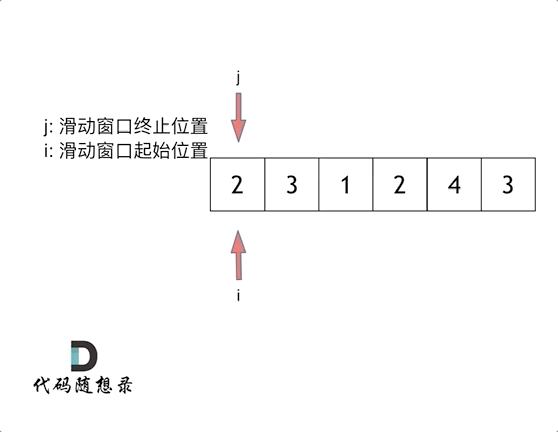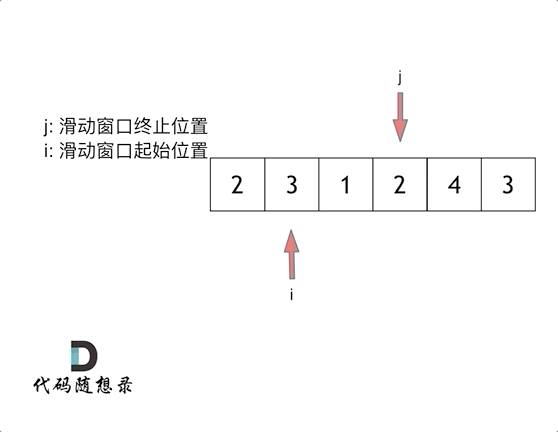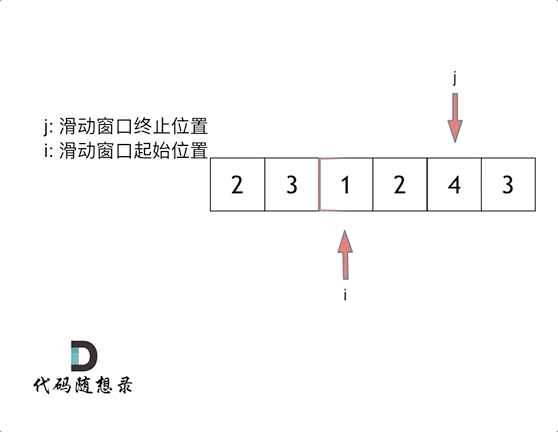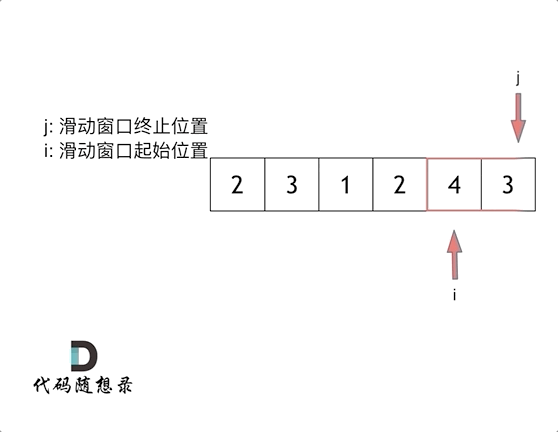
代码

1.暴力破解法

点击查看代码

class Solution {
    public int minSubArrayLen(int target, int[] nums) {
        int subString ;
        int result = Integer.MAX_VALUE;
        int sum ;
        for (int i = 0; i < nums.length; i++) {
            sum =0;
            for (int j = i; j < nums.length; j++) {
                sum +=nums[j];
                if(sum>=target){
                   subString =  j-i+1;//子序列的长度
                   result = result<subString?result:subString;//获取较小子序列的长度
                    break;
                }
            }
        }
        return result= result<Integer.MAX_VALUE?result:0;
    }
}

2.双指针法(滑动窗口)

点击查看代码

class Solution {
    public int minSubArrayLen(int target, int[] nums) {
       int subString ;
       int result = Integer.MAX_VALUE;
       int i=0;
       int sum = 0;
        for (int j = 0; j < nums.length; j++) {
            sum += nums[j];
            while(sum>=target){//while循环用来更新初始位置i
                subString = j-i+1;//获取子序列的长度
                result = result<subString?result:subString;
                sum -= nums[i];//滑动窗口变小
                i++;//缩小窗口
            }
        }
        return result=result<Integer.MAX_VALUE?result:0;
    }
}

总结

两种方法的区别：

• 滑动窗口只遍历了一次数组，并且减少了计算次数(减去起始位置的值就得到新的滑动窗口的值，不用像前者一样重新计算一遍)
  由于在while循环，每个元素在滑动窗后进来操作一次，出去操作一次，每个元素都是被操作两次，所以时间复杂度是 2 × n 也就是O(n)