<1>方程的导出和定解条件

三类方程的导出

1. 弦振动方程和定解条件

物理模型

长为 l 的柔软的、均匀细弦，拉紧后 在垂直于弦线的外力作用下做微小横振动（弦的运动发生在同一平面内，且弦上各点的位移与平衡位置垂直），求在不同时刻弦线的形状。

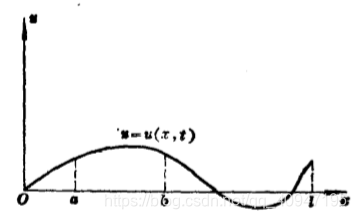
弦振动方程

通过建立如上坐标系，我们得到在任意时刻\(t\) ，弦线上各点的位移为$$u=u(x,t)$$任取一段弦 \([a,b]\) ,通过动量守恒定律，进行一系列的变换，得到弦振动方程(刻画均匀弦的微小横振动)

\[ \frac{\partial^2 u}{\partial t^2}-a^2\frac{\partial^2 u}{\partial x^2}=f(x,t) \qquad (0<x<l,t>0) \]

定解条件（初始条件和边界条件）

一根弦线特定的振动状况还依赖于初始时刻弦线的状态和通过弦线的两端受到的外界的影响
初始条件
给出弦上各点在初始时刻 \(t=0\) 的位移和速度。$$u(x,0)=\psi(x)\qquad(0<x<l)$$$$u_t(x,0)=\phi(x)\qquad(0<x<l)$$边界条件
（1）已知端点的位移变化，即$$u(0,t)=g_1(t),\qquad u(l,t)=g_2(t)$$当\(g_1(t)=0 , g_2(t)=0\) 时，称弦线具有固定端。

（2）已知端点所受的垂直于弦线的外力的作用，即$$-T\frac{\partial u}{\partial x}|{x=0}=g_1(t)$$$$T\frac{\partial u}{\partial x}|=g_2(t)$$当\(g_1(t)=0 , g_2(t)=0\) 时，称弦线具有自由端。
（3）已知端点的位移和所受外力作用的一个线性组合$$-T\frac{\partial u}{\partial x}|{x=0}+a_1u(0,t)=g_1(t)$$$$T\frac{\partial u}{\partial x}|+a_2u(l,t)=g_2(t)$$$$a_i>0,i=1,2$$当\(g_1(t)=0 , g_2(t)=0\) 时，表示弦的两端固定在弹性支承上\(a_i\)表示支承的弹性系数。

定解问题

偏微分方程连同定解条件组成定解问题
弦振动方程的混合问题 = 偏微分方程+初始条件+边界条件（其中一个），
弦振动方程的混合问题 = 偏微分方程+初始条件

2. 热传导方程和定解条件

物理模型

三维空间中，考虑一均匀，各向同性，内部有热源的物体，它与周围介质有热交换，研究该物体内部温度的分布和变化

热传导方程

由能量守恒定律，推出热传导方程：$$\frac{\partial u}{\partial t}-a^2\Delta u=f $$当 \(f\geq 0\) 时表示热源，当 \(f\leq 0\) 时表示热汇。

定解条件

为了具体确定物体内部的温度分布，我们还需要知道物体内部的初始温度分布以及通过物体的边界受周围介质的影响。
初始条件

\[u(x,y,x,0)=\phi(x,y,z),\qquad (x,y,z)\in\bar{\Omega}. \]

边界条件
（1）已知边界 \(\partial\Omega\) 上的温度分布$$u|\Sigma=g(x,y,z,t),$$$$\Sigma=\partial\Omega \times[0,+\infty)$$当 \(g\equiv0\) 时，称物体的边界保持恒温。
（2）已知通过物体边界\(\partial\Omega\) 上的热量，$$k\frac{\partial u}{\partial n}|\Sigma=g(x,y,z,t),\ （n 为 \Omega 的外法向量）$$\(g\geq0\)表示流入，\(g\leq0\)表示流出，当 \(g\equiv0\) 时，表示物体绝缘。
（3）已知通过边界\(\partial\Omega\) 与周围介质有热交换，$$k\frac{\partial u}{\partial n}|\Sigma=a_0(g_0-u)|\Sigma,$$或$$(\frac{\partial u}{\partial n}+au)|_\Sigma=g(x,y,z,t),$$\(g_0\) 表示周围介质温度，\(a_0\) 表示热交换系数，\(a=a_0/k>0\).