P2437 蜜蜂路线 二维数组高精度加法的斐波那契

题目背景

无

题目描述

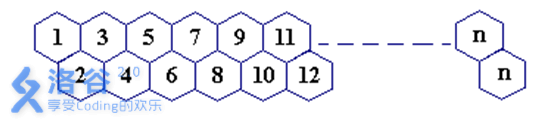
一只蜜蜂在下图所示的数字蜂房上爬动,已知它只能从标号小的蜂房爬到标号大的相邻蜂房,现在问你：蜜蜂从蜂房 m 开始爬到蜂房 n，m<n，有多少种爬行路线？（备注：题面有误，右上角应为 n−1）

输入格式

输入 m,n 的值

输出格式

爬行有多少种路线

输入输出样例

输入 #1

1 14

输出 #1

377

说明/提示

对于100%的数据，M,N≤1000

 

不难发现对于每一个格子来说，都只能从比他小的相邻的两个格子爬过来，也就是说，爬到这个格子的方案数就等于爬到比他小的相邻的两个格子的方案数，显而易见的斐波那契数列，从m爬到n，也就是进行n-m次斐波那契的过程

再看数据范围，1000的fb需要打高精度加法，如果用传统的单维度数组处理，就需要经历字符串转化等一系列复杂过程，那有没有什么简单的方法呢？

 

引入一个概念：二维数组的高精度加法

我们在传统一维数组f[i]的基础上增添一维变为f[i][j]，f[i][j]表示第i个斐波那契数的第j位是多少

举个例子，f[3][1]，{1,1,2},表示的就是第三个斐波那契数的第一位，也就是2，所以f[3][1]=2

再举一个例子，f[7][2],{1,1,2,3,5,8,13}，表示的就是第七个斐波那契数的第二位，也就是3，所以f[7][2]=3

我们直接用第一维进行fb的递推，用第二维进行进位

直接上代码，具体看注释

 

void J(int x)//x表示当前是第几个fb数
{
    for(int i=1;i<=len;i++)//len是当前fb数的位数，初始化len=1
       f[x][i]=f[x-1][i]+f[x-2][i];//每一位求和
    for(int i=1;i<=len;i++)//检查每一位是否需要进位
       {
           if(f[x][i]>9)//如果需要,就进位
           {
               f[x][i+1]+=f[x][i]/10;//当前fb数的下一位
               f[x][i]%=10;
           }
        if(f[x][len+1])len++;//如果len+1位不为空，肯定是被进位了，总位数+1   
       }
}

 

 最后把结果倒序输出就好

 

完整代码

 

#include<bits/stdc++.h>
using namespace std;
int n,m,f[1005][1005],len;
void J(int x)
{
    for(int i=1;i<=len;i++)
       f[x][i]=f[x-1][i]+f[x-2][i];
    for(int i=1;i<=len;i++)
       {
           while(f[x][i]>9)
           {
               f[x][i+1]+=f[x][i]/10;
               f[x][i]%=10;
           }
        if(f[x][len+1])len++;   
       }
}
int main()
{
    cin>>m>>n;
    f[1][1]=1;
    f[2][1]=2;
    len=1;
    for(int i=3;i<=n-m;i++)
       J(i);
    for(int i=len;i;i--)cout<<f[n-m][i];   
       
/*    for(int i=1;i<=n-m;i++)
       {
           for(int j=1;j<=len;j++)
              cout<<f[i][j];
           cout<<endl;   
          }   */
    return 0;
}