PCB 合拼遍历(全排序+旋转90度) 基本遍历方法

     分享一下PCB合拼的组合的遍历方法，在分享之前先纠正一下 PCB拼板之多款矩形排样算法实现--学习  时间复杂度计算错误

 一.PCB 合拼(全排序+旋转90度)的时间复杂度是多少?

二.合拼遍历(全排序+旋转90度)  基本遍历方法 

    1.调用方法

            //准备数据
            List<RectSizeDemo> RectSizeList = new List<RectSizeDemo>();
            RectSizeList.Add(new RectSizeDemo() { Name = "A板" });
            RectSizeList.Add(new RectSizeDemo() { Name = "B板" });
            RectSizeList.Add(new RectSizeDemo() { Name = "C板" });
            //3款板  全排序组合总类     1*2*3=6
            //3款板  旋转90度组合总类   2*2*2=8 
            //3款板  总排样组合         6*8=48种组合
            //计算 PCB旋转90度组合总类
            int PowCount = (int)Math.Pow(2, RectSizeList.Count()) - 1;
            //执行PCB 合拼遍历(全排序+旋转90度)
            RectSizeDemo.Loop(RectSizeList, PowCount, 0, RectSizeList.Count - 1); 

    2.合拼遍历方法类(全排序+旋转90度)

    /// <summary>
    /// 全排序+旋转90 示例
    /// </summary>
    public class RectSizeDemo
    {
        /// <summary>
        /// PCB板名称
        /// </summary>
        public string Name { get; set; }
        /// <summary>
        /// 成品尺寸
        /// </summary>
        public Size Size { get; set; }
        /// <summary>
        /// 递规全排序+旋转
        /// </summary>
        /// <param name="RectSizeList"></param>
        /// <param name="PowCount"></param>
        /// <param name="k"></param>
        /// <param name="m"></param>
        public static void Loop(List<RectSizeDemo> RectSizeList, int PowCount, int k, int m)
        {
            if (k == m)
            {
                for (int i = 0; i <= PowCount; i++)
                {
                    for (int j = 0; j <= m; j++)
                    {
                        string pnString = (((i >> j) & 1) == 1) ? "旋转0 " : "旋转90";
                        Console.Write($"【{RectSizeList[j].Name} {pnString}】");
                    }
                    Console.WriteLine("");
                }
                Console.WriteLine("===============================");
            }
            else
            {
                for (int i = k; i <= m; i++)
                {
                    Swap(RectSizeList, k, i);
                    Loop(RectSizeList, PowCount, k + 1, m);
                    Swap(RectSizeList, k, i);
                }
            }
        }
       /// <summary>
       /// 交换数据
       /// </summary>
       /// <param name="RectSizeList"></param>
       /// <param name="i"></param>
       /// <param name="j"></param>
        public static void Swap(List<RectSizeDemo> RectSizeList, int i, int j)
        {
            RectSizeDemo t = RectSizeList[i];
            RectSizeList[i] = RectSizeList[j];
            RectSizeList[j] = t;
        }
    }

 

 三. 上面代码,A,B,C三款板运行后效果

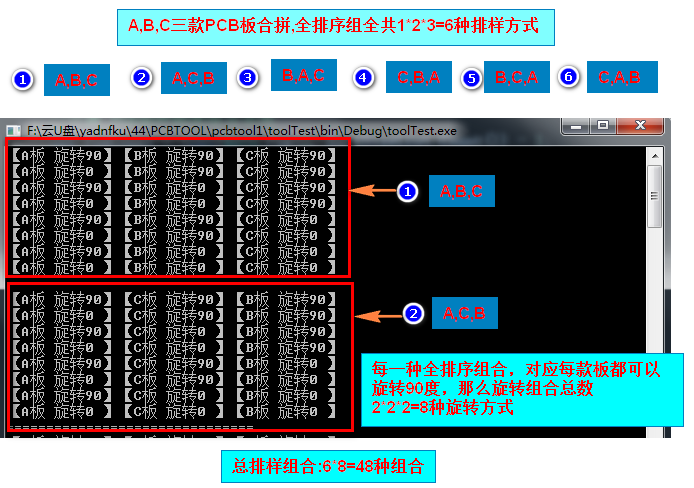
      1.A,B,C三款PCB板合拼,全排序组全共1*2*3=6种排样方式

      2.每一种全排序组合，对应每款板都可以旋转90度，那么旋转组合总数2*2*2=8种旋转方式

      3.总排样组合:6*8=48种组合

 

 四.小结

      当PCB板为10款板，排样组合总类数达到了惊人的37亿种组合，如此大计算量，普通计算机已消化不了这么大计算量了，那么我们可以想像一下,如果PCB合拼是20款板或30款板，再或者PCB合拼中嵌入了各种规则加入排样算法中，此时还想指望计算机能有限时间内计算全部排样方式来是不现实的。当我们遇到组合爆炸问题, 通常会在合拼算法上做一些技巧处理，虽然不能达到全局最优解，但在算法优化上以我们对PCB的合拼排样规则深入了解，可以近可能的的求出近似最优解的。

 

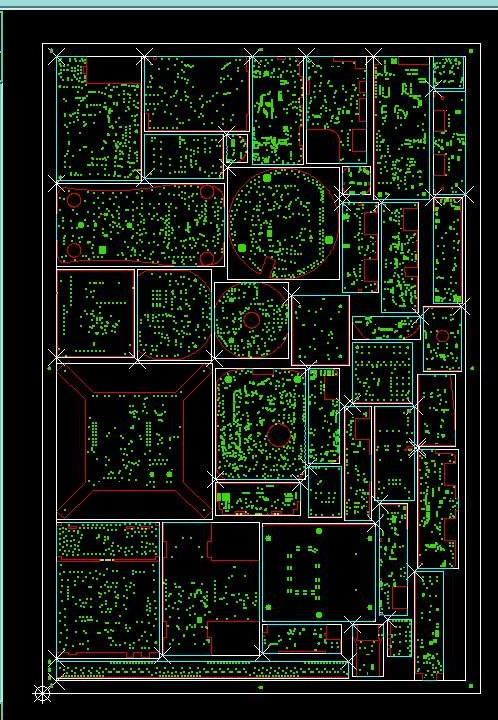
 附上PCB合拼排样方案