KMP模式匹配算法

KMP算法的难点在于next数组的求解。不同的书籍的KMP算法的next数组求解不一样，先看下不同版本的next数组求解结果：

对于模式串P=ababaca

《算法导论》：

 

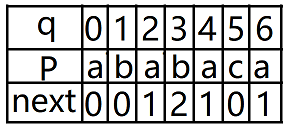
《大话数据结构》：

 

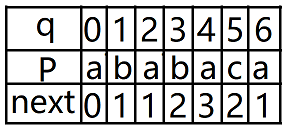
 个人觉得《算法导论》的KMP算法更容易理解些，当然《大话数据结构》的KMP算法也会进行理解分享。

《算法导论》KMP模式匹配算法：

名词与记法：

P_K：模式串ababaca有P₀="",P₁=a,P₂=ab,P₃=aba,P₄=abab,P₅=ababa,P₆=ababac,P₇=ababaca

前缀与后缀：字符串由X和Y拼接而成，记W=XY，X和Y至少含有一个字符，X叫做W的前缀，Y叫做W的后缀。例如，abcd的最长前缀为abc，最短前缀为a，abcd的最大后缀为bcd，最短后缀为d。

next求解公式：

 

C++代码实现：

void AlgorithmGetNextArray(string &P, vector<int>&next)
{
	int q, k;//q为模板字符串下标，k为最大前后缀长度，m为模板字符串长度
	next[0] = 0;//模板字符串的第一个字符的最大前缀长度为0
	for (q = 1, k = 0; q < P.size(); ++q)//从第二个字符开始计算,从头至此字符构成的字符串的最大相同前后缀的长度，即next值
	{
		while (k > 0 && P[q] != P[k])//当前字符串为Pq，最后一个字符为P[q]
			k = next[k - 1];//根据已经求得的next数组回溯，寻找Pq的前后缀交集中最大长度的字符串
		if (P[q] == P[k])//如果前缀的最后一个字符和P[q]相同，最大相同前后缀长度加1
		{
			k++;
		}
		next[q] = k;//Pq最大相同前后缀的长度为k
	}
}

　　

int AlgorithmKMP(string &str, string&P, vector<int>&next)
{
	int i, q;
	AlgorithmGetNextArray(P,next);
	for (i = 0, q = 0; i < str.length(); ++i)
	{
		while (q>0&&P[q]!=str[i])
			q = next[q]-1;
		if (P[q] == str[i])
			q++;
		if (q == next.size())//next数组走完了
			return i - next.size() + 1;
	}
	return -1;
}

　　

 《大话数据结构》KMP匹配算法：

next求解公式：

两种写法，第一种《算法导论》写法：

void DaHuaGetNextArray(string&P,vector<int>&next)
{
	int q,k;
	next[0] = 0;
	for (q = 1, k = 0; q < next.size(); ++q)
	{
		while (k>1&&P[q-1]!=P[k-1])
		{
			k = next[k-1];
		}
		if (k == 0 || P[q - 1] == P[k - 1])
		{
			k++;
		}
		next[q] = k;
	}
}

　　

int DaHuaKMP(string &str, string&P, vector<int>&next)
{
	DaHuaGetNextArray(P,next);
	int i, q;
	for (i = 0, q = 0; i < str.length(); ++i)
	{
		if (str[i] == P[q])
		{
			++q;
		}
		else
			q = next[q];
		if (q == next.size())//next数组走完了
			return i - next.size()+1;
	}
	return -1;
}

　　

 第二种，《大话数据结构》写法：

 草，就是不想加哨兵，暂时不会写不加哨兵的。。。。。。。。。。。。。。。