CF/AT 难题选做

1.CF559E Gerald and Path

题目大意：

有 \(n\) 条线段，每条线段给定其中一端的位置及长度，求所有线段覆盖的最大长度。

\(n \le 100\)

难度：Normal，*3000

大概就是要想着先对一端排序，然后每次钦定当前线段的方向然后去dp。

设计一个 \(dp_{i,j}\) 表示前 \(i\) 条线段，最右端覆盖到位置 \(j\) 时覆盖的最长长度。

转移的时候如果当前向右放就比较好处理，因为再往右没有被覆盖过的了，全是新的贡献。设当前线段固定的端点的位置是 \(p\)，则 \(dp_{i,j}=\max\{dp_{i-1,p}+dist(p,j)\},j\in[p,r]\)。

但是向左放的时候可能会出问题，因为他可能会覆盖到之间没有被覆盖过的部分。（前面的都太短了，而这个特别的长）

借个图：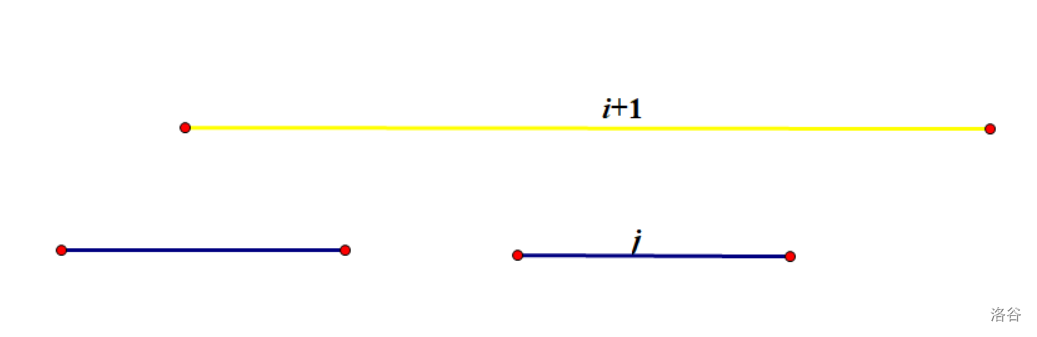

所以为了避免这种情况，我们可以枚举一个 \(k \in [1,i-1]\)，强制钦定 \(\in[k,i-1]\) 的线段都往右放。

令 \(l\) 表示当前这条线段往左放后左端点的位置，\(R\) 表示 \([k,i-1]\) 中所有线段的右端点的最大值，则有 \(dp_{i,j}=\max\{dp_{k-1,l}+dist(l,R)\}\)，正确性可以被感性理解。

2.CF1305G Kuroni and Antihype

剧透别看后面的白字 \(\color{white}\text{~~逛洛谷看到有人在要MST的牛逼题就想到了这个~~}\)

题目大意：

现在有 \(n\) 个人，并且给出他们的年龄。两个人是朋友，当且仅当两个人年龄的按位与结果为 \(0\)。

现在，有一个传销组织，每个人有两种操作：

1、主动加入传销组织，这样的话，传销组织不会给你钱；

2、邀请自己的一个朋友加入传销组织，这样的话，传销组织会奖励你数值等于你的年龄的钱。（当然，执行该操作的人必须已经进入传销组织了）

每个人只可以进入传销组织一次。

现在，请你输出，如果 \(n\) 个人通力合作，传销组织支付给这 \(n\) 个人的钱数之和最大是多少。

难度：Normal+，*3500

妙！难点就一句话，上面的白字。

每个点只能加进这个组织一次，就像一棵树每个节点最多一个父节点一样，难度就在于怎么去构造这个MST。

设 \(a_{n+1}=0\)，且初始这个人已经加入了组织。如果将每个点在 \(2\) 过程中选择的点与它之间连一条边，会得到一棵树。此时将 \(i\) 和 \(j\) 之间的边权设为 \(a_i+a_j\)，那么答案就是最大的边权减去总点权，就是最大生成树。

由于只有两个点与起来为 \(0\) 才会有边，所以加法相当于是或。

这就可以推出一个能过的 \(O(3^{18}\alpha(n))\) 的做法了。从大到小枚举当前考虑到的边权 \(x\) （kruskal基操），然后枚举 \(x\) 的一个子集 \(i\)，将 \(i\) 和 \(x \oplus i\) 连起来。

此题还有 \(O(18\times2^{18} \log n)\) 的做法，留给读者自行思考。（用哪个啥B开头的MST算法）

3.CF1188D Make Equal

题目大意：

给出 $ n $ 个数字 $ a_1 , a_2 , \ldots , a_n $ ，每次操作可以给其中一个数加上 $ 2 $ 的非负整数次幂。求最少的操作次数，使得这 $ n $ 个数相等。

\(1 \le n \le 10^5\)

难度：Hard-，*3100

我不会做，降智。

一个显然的（对我来说并不显然）的转化是要变为求 \(\sum{x+a_n-a_i}\) 的类型。（让 \(a\) 按照从小到大排序）

下面让 \(a_i\) 变为 \(a_n-a_i\)。（我怎么想不到啊）

从小到大决策当前这个 \(x\) 的第 \(k\) 位，有 \(3\) 个相关的量：

• \(x\) 这一位是不是 \(1\)

• \(a\) 中有多少个数这一位是 \(1\) （接下来会产生进位）

• 前面 \(k-1\) 为的进位对这一位产生的贡献

前两个好处理，就是第三个不好处理。

如果 bitmask 枚举前面那些数，那么复杂度就爆炸了（\(2^n\)），显然过不去。

又是一个对我来说不显然的结论，就是对于最低的 \(k-1\) 位来说，对第 \(k\) 位产生进位的一定是那些 \(a\) 中对 \(2^{k-1}\) 取模后从大到小排序的一个前缀。证明显然。

令 \(dp_{i,j}\) 表示考虑了最低的 \(i\) 位，上一位有 \(j\) 个进位时的答案。

可以发现我们不关心这个数到底是多少，只关心 \(1\) 的数量和进位的数量

令 \(cnt\) 为 \(a\) 中这一位数中 \(1\) 的总数，\(tot\) 为前 \(j\) 个数这一位 \(1\) 的总数。

• 上次进位，这一位是 \(1\)，有 \(tot\) 个。
• 上次进位，这一位是 \(0\)，有 \(j-tot\) 个。
• 上次未进位，这一位是 \(1\)，\(cnt-tot\) 个。
• 上次未进位，这一位是 \(0\)，\(n-j-(cnt-tot)\) 个。

这一位取 \(1\)，则 \(1,2,3\) 进位，\(1,4\) 这一位是 \(1\)。

这一位取 \(0\)，则 \(1\) 进位，\(2,3\) 这一位是1。

没了。有就是这玩意和基数排序很像，这么写可以减小常数。

4.CF739E Gosha is hunting

题目大意：

你要抓神奇宝贝！
现在一共有 \(n\) 只神奇宝贝。
你有 \(a\) 个『宝贝球』和 \(b\) 个『超级球』。
『宝贝球』抓到第 \(i\) 只神奇宝贝的概率是 \(p_i\)，『超级球』抓到的概率则是 \(u_i\)。
不能往同一只神奇宝贝上使用超过一个同种的『球』，但是可以往同一只上既使用『宝贝球』又使用『超级球』（都抓到算一个）。
请合理分配每个球抓谁，使得你抓到神奇宝贝的总个数期望最大，并输出这个值。

\(n \leq 2000\)。

我可以出到 \(n \le 10^5\)。

难度：Easy--，*3000

就这也配*3000？？？

裸的wqs二分，套一次可以做到 \(n^2\log n\) 过原题，套两次就可以做到 \(n\log ^2n\) 过 \(1e5\)。

那就简单写一下什么是wqs二分。

原题没有代价只有次数限制，现在我们想办法取消这个次数限制。

如果直接取消那么肯定是全部用掉最优，所以我们对每次用就加上一个代价。

然后二分这个代价，直到贪心（或者dp）后得到使用的次数和限制相同且答案最大。

5.CF1463F Max Correct Set

题目大意：

规定一组正整数 \(S\)。当且仅当满足以下条件时该组正整数成立：

• \(S \subseteq \{1,2,...,n\}\)

• 如果 \(a \in s\) 并且 \(b \in s\)，那么 \(|a - b| \not ={x}\) 并且 \(|a - b| \not ={y}\)

对于给定的数值 \(n,x,y\)，你需要找到成立数组的最大长度。

\(1 \le n \le 10^9, 1 \le x,y \le 22\)

难度：Normal+，*3100

神奇的思维题，和我之前做过的一道MO题好像？？？

结论是可以有个长度为 \(x+y\) 的循环节。钦定 \(x \ge y\)，然后令 \(dp_{i,j}\) 表示考虑到了第 \(i\) 位，最后 \(x\) 位的 mask 位 \(j\) 时的答案。（这样我们只用存 \(x\) 位而不是 \(x+y\) 位了，是个trick）

证明挺难的，可以参考 7KByte大爷的 或者 feecle6418大爷的 。

6.CF1616H Keep XOR Low

题目大意：

给你 \(n\) 个整数 \(a_1,a_2,\cdots,a_n\) 和一个整数 \(x\)。

你需要求出 \(\{1,2,\cdots,n\}\) 的一个子集 \(S\)，满足 \(S\) 中任意两个不同的元素 \(i,j\)，满足 \(a_i~{\rm xor}~a_j\le x\)。

求选取 \(S\) 的方案数，对 \(998244353\) 取模的结果。

\(1\le n\le 150000,0\le a_i,x< 2^{30}\)

难度：Normal+（可能我不熟悉这类题），*3000

一眼异或，鉴定为 01-trie。设计 \(dp_{u}\) 表示考虑到以 \(u\) 为根的子树中，两两异或都 \(\le x\) 的方案数。

这么dp会寄掉，应为当这一位是 \(1\) 的时候它的两个子树间互相还有限制。

怎么办？大胆点，令 \(dp_{u1,u2}\) 表示在 \(u1\) 和 \(u2\) 中选若干个数，两两异或都 \(\le x\) 的方案数。

看起来这个玩意很扯淡，但是是可行的。（记当前考虑到第 \(d\) 层）

若 \(x\) 的第 \(d\) 位为 \(1\)，那么 \(u1\) 的左儿子和 \(u2\) 的左儿子的子树内的数异或起来一定不会大于 \(x\) 了，\(u1\) 的右儿子和 \(u2\) 的右儿子同理。所以现在我们只需要考虑 \(u1\) 的左儿子和 \(u2\) 的右儿子，以及 \(u2\) 的左儿子和 \(u1\) 的右儿子之间的限制，直接把两个 \(dp\) 值乘一下就行了。

若 \(x\) 的第 \(d\) 位为 \(0\)，那么 \(u1\) 的左儿子和 \(u2\) 的右儿子不能同时选数，\(u1\) 的右儿子和 \(u2\) 的左儿子同理。所以把这两个dp值加一下，再加上单独在某个儿子里选数的方案就可以了。

7.[AGC024F] Simple Subsequence Problem

题目大意：

有一个 01 串集合 \(S\)，其中每个串的长度都不超过 \(N\)，你要求出至少是 \(S\) 中 \(K\) 个串的子序列的最长串，如果有多解，输出字典序最小的那组解。

由于 \(S\) 可能很大，因此我们是这样描述 \(S\) 的：

• 你将得到 \((N+1)\) 个 01 串，第 \(i\) 个串的长度为 \(2^{i-1}\)。

• 第 \(i\) 个字符串的第 \(j\) 个字符，代表数字 \((j-1)\) 的、长度为 \((i-1)\) 的二进制表示是否出现在 \(S\) 中。

\(N \leq 20\)。

难度：Hard（？），difficulty 3544

这是我的子序列自动机入门题。

题目相当于对于每个串，对其所有子序列的值+1，问你最后所有可能的01串的值的最大值是多少。

我们不可以枚举每个串的所有子序列，所以这之后就要用到一个叫做子序列自动机的玩意。

考虑如何贪心的去确定一个01串是不是另外一个01串的子序列。假设当前匹配串的开头是 \(p\)，那么我们要在模式串中找到开头第一个 \(p\) 去和他对应。

所以我们就可以模拟这个过程，令 \(A\) 为当前已经匹配好的串，\(B\) 为模式串剩余的部分，然后可以发现每种状态有两种出路（把模式串的开头匹配掉和从头开始第一个和开头不同的字符匹配掉）。

由于 \(|A+B|\le 20\)，所以我们就可以记录 \(|A+B|\) 和 \(A+B\)，然后dp的时候枚举 \(A\) 的长度，就可以方便的转移了（这样做可以直接省掉两个开头互相匹配的情况，十分方便）

参考代码

8.[AGC016F] Games on DAG

题目大意：

给定一个\(n\)个点\(m\)条边的DAG，对于每条边\((u,v)\)都满足\(u<v\)，\(1,2\)号点各一个石头，每次可以沿DAG上的边移动一颗石头，不能移动则输，求所有\(2^{m}\)个边的子集中，只保留这个子集先手必胜的方案个数

难度：Normal（？）,difficulty 3754

我的博弈论入门题

这题本质上就是要求SG(1) 和 SG(2) 不相同，然后可以转化为 \(2^m\) 减去相同的情况。

SG(i) 的定义：它的所有邻居的SG()的mex

所以我们就可以每次枚举新的SG()值为0的点，要求满足他们之间不能互相连边，之前枚举的所有不是0的点至少要向这些点中的一个点连边，这些点向不是0的点的连边没有要求

然后就是1号点和2号点要么同时在不是0的点，要么同时是新的0。

这是个子集枚举，复杂度 \(O(n\times3^n)\)

9.CF1149D Abandoning Roads

题目大意：

一张 \(n\) 个点 \(m\) 条边的无向图，只有 \(a,b\) 两种边权（\(a<b\)），对于每个 \(i\)，求图中所有的最小生成树中，从 \(1\) 到 \(i\) 距离的最小值。

\(n \le 70\)

难度：Hard++++，*3000

溜去看题解了。

你告诉我这只有3000？？？

这复杂度是人能想出来的？？？？

由于是在所有最小生成树中，所以有这么一个性质：一条连续的全为 \(a\) 的路径肯定会出现在至少一棵MST中。

就有了这么一个结论：如果把原图中所有重边删掉，会剩下一些联通块。一条路径可能在最小生成树上，当且仅当它没有离开一个联通块后再回到原来那个联通块中。

然后就是令 \(dp_{u,S}\) 表示考虑已经走了状压后集合为 \(S\) 的连通块，当前走到 \(U\) 时最短路径的长度。转移用最短路转移。

这个方法时 \(O(2^n\log(2^n(n+m)))\) 的，铁定过不去。

但是现在还有这么一个结论：我们不用考虑所有大小 \(\le 3\) 的连通块，因为这种连通块我们就算不把它压进去，它光是靠dijkstra就可以把它排除不会再进来了。（出去再回来至少要 \(2\times b\)，而内部光靠 \(a\) 就可以做到 \(2\times a\)，更优）

结束了。妙死了啊！时间复杂度 \(O(2^{\frac{n}{4}}\log(2^{\frac{n}{4}} +m))\)，如果用01bfs代替dijksta可以砍掉这个 \(\log\)。

10.APC001F XOR Tree

题目大意：

给你一棵有\(N\)个节点的树，节点编号从\(0\)到\(N-1\)，
树边编号从\(1\)到\(N-1\)。第\(i\)条边连接节点\(x_i\)和\(y_i\)，其权值为\(a_i\)。

你可以对树执行任意次操作，每次操作选取一条链和一个非负整数\(x\)，将链上的边的权值与\(x\)异或成为该边的新权值。

问最少需要多少次操作，使得所有边的权值都为0。

\(2\leq N \leq 10^5 , 0\leq a_i \leq 15\)

难度：easy-，difficulty 2865

就这也能黑题？洛谷恶评严重。

一个套路是将比边权下放到点权，令每个点的点权为它周围一圈边的权值的异或和。

现在如果对一条 \(u\) 到 \(v\) 的路径做异或，那么就相当于对点 \(u\) 和 \(v\) 的权值做异或，最终目标就是让所有点的权值都为 \(0\)。

最后就是玩消消乐，消完以后每种权值的数量不会超过 \(1\)，子集dp一下就行了。

11.CF232E Quick Tortoise

题目大意：

在一个 \(n \times m(1 \le n,m\le 500)\) 的网格上，有一些格子是障碍。给定 \(q(1\le q \le6\times10^5)\) 个询问，每次询问是否能只通过向下走和向右走从格子 \((x_1,y_1)\) 走到格子 \((x_2,y_2)\)。

难度：Normal，*3000

有点套路的题，考虑分治。

如果当前这些询问中满足存在一行使得所有询问可能的路径都必须经过这一行的一个点，那么这些询问可以在 \(O(\frac{n^3}{\omega}+\frac{qn}{\omega})\) 的时间内完成。我们可以对这个网格上的每一个点维护一个bitset，第 \(i\) 为表示能不能到那一行（所有询问必须经过的那一行）的第 \(i\) 个点，转移的话随便或一下就可以了。

然后就可以分治了。起点和终点都在 \(mid\) 行上面、都在 \(mid\) 下面、剩下的都是必须经过 \(mid\) 行的。

12.CF1707E Replace

题目大意：

给定一个长为 \(n\) 的序列 \(a_1,\ldots,a_n\)，其中对于任意的 \(i\) 满足 \(1 \leq a_i \leq n\)。

定义一个二元组函数如下：

\[f((l,r)=(\min\{a_l,\ldots,a_r\},\max\{a_l,\ldots,a_r\})(l \leq r) \]

你需要回答 \(q\) 次询问，每次给定 \((l_i,r_i)\)，问其最少经过多少次 \(f\) 的调用（即 \((l,r) \rightarrow f((l,r))\)）使得 \((l_i,r_i)\) 变成 \((1,n)\)，若无解请输出 -1。

难度：Hard++，清新思维题，*3500

这题中有区间max/min，就很自然的想到了ST表和倍增。

如果裸的倍增会很烦，因为有 \(n^2\) 种区间，寄。

考虑能不能用类似ST表的方法来处理，就是用两个较大的、有交集的区间并称一个大区间，就能将 \(n^2\) 缩小为 \(n\log n\) 了。

注意到 \(f(l,r)=f(l,l+1)\cup f(l+1,l+2)\cup\dots f(r-1,r)\)，然后可以证明 \(f^k(l,r)=f^k(l,l+1)\cup f^k(l+1,l+2)\cup\dots f^k(r-1,r)\)，这就可以用倍增维护了。

13.CF1710D Recover the Tree

题目大意：

你需要根据题目给出的信息构造出一棵树，满足如下条件：

1. 树的节点个数为 \(n\)。

2. 对于每个区间 \([l,r]\) 给出是或不是连通块。

数据保证有解，\(n\le 2000\)。

难度：Normal++，*3400

好题。

我们从小到大考虑所有可能的区间（类似区间dp的套路）。

假设我们当前考虑到有一个联通的区间 \([l,r]\)，其中他们分别属于 \([x_1,x_2-1],[x_2,x_3-1]\dots [x_{k-1},x_k-1]\)，其中 \(l \geq x_1, r\le x_k-1\)。可以发现 \(k\) 为 \([l,r]\) 中所有点属于的不同的连通块个数。如果 \(k=3\) 的时候可以发现无解，\(k=2\) 的时候可以直接连接 \((l,r)\)，如果 \(k>3\) 的时候可以这么连接：\((l,x_{k-1}-1), (x_i,r)(i < k-1)\)。这样就可以保证 \(l\) 和 \(r\) 前面一个连通块之间的所有连通块不能构成一个大的连通块，而 \(l\) 到 \(r\) 就可以了。

14.CF1616G Just Add an Edge

这场的H也在这篇blog中，是#6，但应该没有这个G难/hsh

题目大意：

给定一个 DAG，边一定从编号小的点连向编号大的点，求有多少对 \((x,y)\) 使得 \(x>y\) 且添加 \((x,y)\) 这条边后的图存在哈密顿路径。

\(n \le 150000\)

难度：Hard+(*114514)，不会！

先咕着，明天中午看题解。

我超，终于看懂了，神仙题。

\(n^2\) 暴力很trivial。唯一的路径方式比较显然，就是 \(1 \rightarrow x-1 \rightarrow y-1 \rightarrow x \rightarrow y \rightarrow n\)，其中 \(y-1 \rightarrow x\) 是一步到位，\(1 \rightarrow x-1\) 和 \(y \rightarrow n\) 是一步一步跳。

所以我们可以枚举 \(y\) 考虑有多少个 \(x\) 满足条件。令 \(f_{i,0/1}\) 表示考虑到一个位置 \(i\)，能否由当前枚举的 \((y-1,y)\) 走到 \((i-1,i)\) 或者 \((i,i-1)\)，转移显然。

考虑怎么优化。我们找到一个最靠做的 \(p\) 满足 \(p-1\) 和 \(p\) 之间没有边，此时 \(p\) 即为必经之路。我们可以将这 \(n\) 个数断开来，左边和右边分别dp，然后容斥一下答案就行了。

证明可达的话，如果左边的 \((a,a+1)\) 能到 \((p,p+1)\)，\((p,p+1)\) 能到右边的 \(b,b+1\)，那么显然 \((a,a+1)\) 能到 \((b,b+1)\)，反之 \((p+1,p)\) 同理。

注意一些细节。以及注意当 \(p=2\) 时不好定义 \(f_{0,0/1}\)，所以这才是要加上 \(0\) 和 \(n+1\) 两个虚点的理由。

15.[AGC010E] Rearranging

题目大意：

有一个 \(n\) 个数组成的序列 \(a_i\)。

高桥君会把整个序列任意排列，然后青木君可以进行任意次操作，每次选择两个相邻的互质的数交换位置。

高桥君希望最终序列的字典序尽量小，而青木君希望字典序尽量大。求最终序列。

\(n \le 2000\)

难度：Normal，difficulty 3887

有这么难吗？洛谷和AT都恶评？我独立切了好吧。

哦等下我不会证明这个结论/qd

反正就是说，我们考虑建立图论模型。如果 \(a_i\) 和 \(a_j\) 不互质，那么怎么交换 \(a_i\) 和 \(a_j\) 之间的相对位置也不会改变。

所以，第一个人的操作就相当于对这个无向图定向，第二个人的擦欧总相当于求出这张DAG的一个最大拓扑序。

手玩以后可以发现结论：对于每个连通块，我们从最小的一个数入手，每到一个点 \(x\)，从小到大枚举其所有邻居 \(y\)，搜 \(y\)，并把 \(x\) 指向 \(y\)。

然后用个priority_queue进行topsort就行了。

证明：贺的。