2017-2018 ACM-ICPC, Asia Daejeon Regional Contest 题解
这次 Namomo Summer Camp 2021 Day2 模拟选了这场
这场我们队AK了,排名6/107
讲个笑话,AK的全是中学生队伍,真正的大学生队伍没有一个AK的/youl
upd: 把队友写的题也补上了 现在全场题解都有了
Problem A. Broadcast Stations
通过队伍数:12/107
队友口述做法我写掉了
4h58min 通过,全场所有提交中最后一个AC记录/youl
题目大意:
有一棵 \(n \le 5000\) 个节点的树。你可以对每一个节点赋上一个权值。
假设对于第 \(i\) 个节点,权值赋为 \(x_i\),那么这个节点可以“覆盖”到所有与它距离不超过 \(x_i\) 的点。问你要使得这棵树上所有点都被覆盖到的所有点的总权值是多少。
解法:
考虑树形dp。
令 \(f_{i,j}\) 表示考虑到以 \(i\) 为根的子树,子树中选择的权值最大能够影响到\(i\) 的 \(j\) 辈祖先的最小的权值。
然后发现不方便转移
再设 \(g_{i,j}\) 表示考虑到以i为根的子树 \(j\) 层以下的都能被覆盖的最小代价。
然后我们就可以愉快的推出转移方程了
#include<bits/stdc++.h>
#pragma GCC optimize (2)
#pragma G++ optimize (2)
#pragma GCC optimize (3)
#pragma G++ optimize (3)
using namespace std;
const int mxn=5005;
int n;
vector<int>G[mxn];
int f[mxn][mxn];//f[i][j]表示考虑到以i为根的子树 向上覆盖k层的最小代价
int g[mxn][mxn];//g[i][j]表示考虑到以i为根的子树 j层以下的都能被覆盖的最小代价
inline void dfs(int u,int fa=0){
for(int i=0;i<=n;++i)f[u][i]=g[u][i]=n;
vector<int>sum;sum.clear();
for(int i=0;i<=n+1;++i)sum.push_back(0);
for(int i=0;i<G[u].size();++i){
int v=G[u][i];
if(v==fa)continue;
dfs(v,u);
for(int j=0;j<=n;++j)sum[j]+=g[v][j];
}
for(int i=0;i<G[u].size();++i){ //让子树中的一个能够覆盖到节点u
int v=G[u][i];
if(v==fa)continue;
for(int j=0;j<n;++j)f[u][j]=min(f[u][j],f[v][j+1]+sum[j]-g[v][j]);
}
for(int i=1;i<=n;++i)f[u][i]=min(f[u][i],sum[i]+i);//自己赋上权值
for(int i=n-1;i>=0;--i)f[u][i]=min(f[u][i],f[u][i+1]);
for(int i=1;i<=n;++i)g[u][i]=min(g[u][i],sum[i-1]); //根据定义
g[u][0]=f[u][0];
for(int i=1;i<=n;++i)g[u][i]=min(g[u][i],g[u][i-1]);
}
int main(){
scanf("%d",&n);
for(int i=1;i<n;i++){
int a,b;
scanf("%d%d",&a,&b);
G[a].push_back(b);
G[b].push_back(a);
}
dfs(1);
printf("%d\n",f[1][0]);
}
Problem B.Connect3
通过队伍数:53/107
题目大意:
有一个 \(4 * 4\) 的棋盘。黑白两个人轮流操作。每个人每一次可以选择一列,然后在这一列行最小的地方放上他对应的棋子。如果一个人有 \(3\) 个棋子在横或竖或斜上连在了一起,那么他就赢了,游戏结束。黑先白后。
现在告诉你黑棋第一步走了 \((1,x)\),白棋最后一步走了 \((a,b)\) 且在这一步后赢了,问你最终的局面所有可能的转态的总数。
题解:
直接爆搜
写了份屎山代码莽过去了
#include<bits/stdc++.h>
#define ll long long
#define mp make_pair
using namespace std;
bool been[43046888];
int a,b;
inline int getstate(vector<vector<int> >v){
int rt=0;
for(int i=0;i<4;++i)for(int j=0;j<4;++j)rt=(rt*3)+v[i][j];
return rt;
}
inline vector<vector<int> >reget(int state){
vector<vector<int> >v;
v.resize(4);
for(int i=0;i<4;++i)v[i].resize(4);
for(int i=3;~i;--i)for(int j=3;~j;--j)v[i][j]=state%3,state/=3;
return v;
}
int ans;
inline int win(vector<vector<int> >v){
for(int i=0;i<4;++i){
if(v[i][0]==1 and v[i][1]==1 and v[i][2]==1)return 1;
if(v[i][0]==2 and v[i][1]==2 and v[i][2]==2)return 2;
if(v[i][3]==1 and v[i][1]==1 and v[i][2]==1)return 1;
if(v[i][3]==2 and v[i][1]==2 and v[i][2]==2)return 2;
}
for(int j=0;j<4;++j){
if(v[0][j]==1 and v[1][j]==1 and v[2][j]==1)return 1;
if(v[0][j]==2 and v[1][j]==2 and v[2][j]==2)return 2;
if(v[3][j]==1 and v[1][j]==1 and v[2][j]==1)return 1;
if(v[3][j]==2 and v[1][j]==2 and v[2][j]==2)return 2;
}
if(v[0][0]==1 and v[1][1]==1 and v[2][2]==1)return 1;
if(v[0][0]==2 and v[1][1]==2 and v[2][2]==2)return 2;
if(v[3][3]==1 and v[1][1]==1 and v[2][2]==1)return 1;
if(v[3][3]==2 and v[1][1]==2 and v[2][2]==2)return 2;
if(v[1][0]==1 and v[2][1]==1 and v[3][2]==1)return 1;
if(v[1][0]==2 and v[2][1]==2 and v[3][2]==2)return 2;
if(v[0][1]==1 and v[1][2]==1 and v[2][3]==1)return 1;
if(v[0][1]==2 and v[1][2]==2 and v[2][3]==2)return 2;
if(v[0][2]==1 and v[1][1]==1 and v[2][0]==1)return 1;
if(v[0][2]==2 and v[1][1]==2 and v[2][0]==2)return 2;
if(v[1][3]==1 and v[2][2]==1 and v[3][1]==1)return 1;
if(v[1][3]==2 and v[2][2]==2 and v[3][1]==2)return 2;
if(v[0][3]==1 and v[1][2]==1 and v[2][1]==1)return 1;
if(v[0][3]==2 and v[1][2]==2 and v[2][1]==2)return 2;
if(v[3][0]==1 and v[1][2]==1 and v[2][1]==1)return 1;
if(v[3][0]==2 and v[1][2]==2 and v[2][1]==2)return 2;
return 0;
}
inline void dfs(int state,int turn){
if(been[state])return;
been[state]=1;
vector<vector<int> >v=reget(state);
if(win(v)==1)return;
if(v[a][b]){
if(turn==1 and v[a][b]==2 and win(v)==2){
++ans;
// cerr<<"---------------------------\n";
// for(int i=0;i<4;++i){
// for(int j=0;j<4;++j)cerr<<v[i][j]<<' ';
// cerr<<'\n';
// }
}
return;
}
if(win(v)==2)return;
for(int i=0;i<4;++i){
for(int j=0;j<4;++j){
if(v[i][j]==0){
v[i][j]=turn;
dfs(getstate(v),3-turn);
v[i][j]=0;
break;
}
}
}
}
inline void solve(){
int x;
cin>>x>>a>>b;
--x,--a,--b;
swap(a,b);
vector<vector<int> >v;
v.resize(4);
for(int i=0;i<4;++i)v[i].resize(4);
v[x][0]=1;
dfs(getstate(v),2);
cout<<ans<<'\n';
}
int main(){
ios_base::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
int T;T=1;
// cin>>T;
for(;T--;)solve();号。
}
Problem C.Game Map
通过队伍数:86/107
题目大意:
给你一张无向图。你需要找到一个路径\(c_{1\dots len}\) 满足对于所有的\(1 \le i < len\) 满足 \(nei_{c_i}<nei_{c_{i+1}}\),其中 \(nei_i\) 表示 \(i\) 号节点的邻居数量。
题解:
签到题2号。
我们考虑记忆化搜索。令 \(dp_i\) 表示考虑到当前以 \(i\) 号节点为起始点的最长路径的长度是多少。
很显然这是没有后效性的,因为节点 \(i\) 能辗转或直接到另一个节点 \(j\) 当且仅当\(nei_i<nei_j\),就不存在环状转移。
#include<bits/stdc++.h>
#define ll long long
#define mp make_pair
using namespace std;
const int mxn=1e5+5;
vector<int>g[mxn];
int n,m;
int nei[mxn];
int dp[mxn];
inline int dfs(int x){
if(~dp[x])return dp[x];
dp[x]=1;
for(int i=0;i<g[x].size();++i){
int y=g[x][i];
if(nei[y]>nei[x])dp[x]=max(dp[x],dfs(y)+1);
}
return dp[x];
}
inline void solve(){
cin>>n>>m;
for(int i=1,u,v;i<=m;++i){
cin>>u>>v;
g[u].push_back(v);
g[v].push_back(u);
++nei[v],++nei[u];
}
int ans=0;
memset(dp,-1,sizeof(dp));
for(int i=0;i<n;++i)ans=max(ans,dfs(i));
// for(int i=0;i<n;++i)cerr<<dp[i]<<' ';cerr<<'\n';
cout<<ans<<'\n';
}
int main(){
ios_base::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
int T;T=1;
// cin>>T;
for(;T--;)solve();
}
Problem D.Happy Number
通过队伍数:100/107
真·签到题
给你一个数。
定义一次操作为把一个数 \(x\) 变成它每一位上的数字的平方之和。
比如:\(114\) 操作一次之后变为 \(1^2+1^2+4^2=1+1+16=18\)
定义一个数是 Happy Number 当且仅当经过若干次操作后会变为 \(1\)。
如:\(19->82->68->100->1\)
反之,就是 Unhappy Number
题目告诉你如果是 Unhappy Number 那一定会陷入一个循环
现在给你一个数 \(x \le 10^9\) 让你判断它是不是Happy Number
题解:
暴力即可。
虽然 \(x\le 10^9\)
但一次操作后就 \(\le 9 \times 9^2 = 729\)
可以发现无论怎么样也不会超过 \(10^3\) 了。
然后由于会循环,直接暴力即可。
#include<bits/stdc++.h>
#define ll long long
#define mp make_pair
using namespace std;
map<ll,int>used;
inline void solve(){
ll n;
cin>>n;
while(1){
ll t=0;
for(;n;){
t+=(n%10)*(n%10);
n/=10;
}
if(t==1){
cout<<"HAPPY\n";
return;
}
if(used[t]){
cout<<"UNHAPPY\n";
return;
}
n=t;
used[t]=1;
}
}
int main(){
ios_base::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
int T;T=1;
// cin>>T;
for(;T--;)solve();
}
Problem E.How Many to Be Happy?
通过队伍数:27/107
题目大意:
给你一张 \(n\) 点 \(m\) 边的带权无向图
令 \(H(x):1\le x \le m\) 为让第 \(x\) 条边能在最小生成树中最小需要删除的边数。
你现在需要求出 \(\sum\limits_{i=1}^mH(i)\)
\(1 \le n \le 100, \ 1 \le m \le 500\)
题解:
我们观察对于第 \(i\) 条边(连接 \(u_i,v_i\) ,权值为 \(w_i\) ),它要在最小生成树中需要满足什么条件。
按照 Kruskal 的思路,按照边权从小到大依次加边。那么所有边权 \(\geq w_i\) 的边就没有影响不用考虑了。
然后考虑第 \(i\) 条边什么时候能有用:就是在这之前 \(u_i,v_i\) 不在一个连通块中。
稍微想一下就相当于在原图中求一个最小割。
以 \(u_i\) 为源点,\(v_i\) 为汇点,所有权值 \(< w_i\) 的边都加上,容量为1。
在这张无向图上跑一遍最大流就行了。
注意是无向图,在建图的时候正边和反边的容量都是1。
#include<bits/stdc++.h>
#define ll long long
#define mp make_pair
using namespace std;
#include<bits/stdc++.h>
#define ll long long
#define reg register
#define mp make_pair
#define ri register ll
#define ld long double
using namespace std;
const ll mxn=2e5+5;
ll n,m,s,t;
struct edge{ll to,cap,rev;};
vector<edge>g[mxn];
inline void add_edge(ll from,ll to,ll cap){
g[from].push_back((edge){to,cap,g[to].size()});
g[to].push_back((edge){from,cap,g[from].size()-1});//无向图
}
ll iter[mxn],lev[mxn];
const ll inf=21474836477777;
inline void bfs(){
memset(lev,-1,sizeof(lev));lev[s]=0;
queue<ll>q;for(;q.size();)q.pop();q.push(s);
for(;q.size();){
ll p=q.front();q.pop();
for(ll i=0;i<g[p].size();++i){
edge&e=g[p][i];
if(e.cap>0 and lev[e.to]<0){
lev[e.to]=lev[p]+1;
q.push(e.to);
}
}
}
}
inline ll dfs(ll v,ll t,ll f){
if(v==t)return f;
for(ll&i=iter[v];i<g[v].size();++i){
edge&e=g[v][i];
if(e.cap>0 and lev[e.to]>lev[v]){
ll d=dfs(e.to,t,min(f,e.cap));
if(d>0){
e.cap-=d;
g[e.to][e.rev].cap+=d;
return d;
}
}
}
return 0;
}
inline ll dinic(){
ll flow=0;
for(;;){
bfs();
if(lev[t]==-1)return flow;
memset(iter,0,sizeof(iter));
ll f=0;
for(;;){
f=dfs(s,t,inf);
if(!f)break;
flow+=f;
}
}
return flow;
}
vector<pair<pair<int,int>,int> >E;
inline void solve(){
cin>>n>>m;
for(int i=1,u,v,w;i<=m;++i)cin>>u>>v>>w,E.push_back(mp(mp(u,v),w));
ll ans=0;
for(int i=0;i<m;++i){
memset(g,0,sizeof(g));
s=E[i].first.first,t=E[i].first.second;
int f=E[i].second;
for(int j=0;j<E.size();++j){
if(i==j)continue;
if(E[j].second<f)add_edge(E[j].first.first,E[j].first.second,1ll);
}
ans+=dinic();
}
cout<<ans<<'\n';
}
int main(){
ios_base::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
int T;T=1;
// cin>>T;
for(;T--;)solve();
}
Problem F.Philosopher’s Walk
通过队伍数:74/107
题目大意:
/youl
时间全花在看懂上
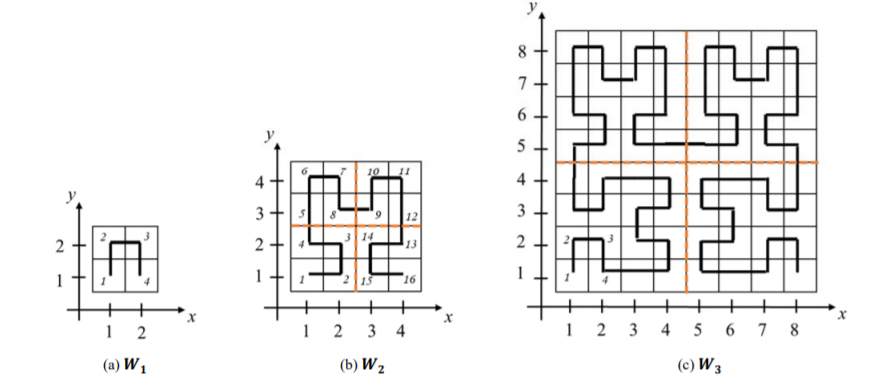
这分别是 \(1\) 阶 \((n=2)\),\(2\) 阶 \((n=4)\) 和 \(3\) 阶 \((n=8)\) 的情况。
现在给你 \(n\) 是\(2^t\) ( \(t\le 15\)是正整数)和 \(k\),让你求出 \(t\) 阶图中第 \(k\) 个点的位置在哪
解法:
理解题意后可以发现大图是由小图转化而来。
所以我们可以不断的翻折、平移坐标系,从小往大推。
一个基础图形:左下->左上->右上->右下
递归小的后返回大的时考虑如何变化坐标系即可。
#include<bits/stdc++.h>
#define ll long long
#define mp make_pair
using namespace std;
inline pair<int,int> dfs(ll n,ll k){
if(k==0)return mp(0,0);
int per=n*n/4;
int t=k/per,res=k%per;
pair<int,int> p=dfs(n>>1,res);
if(t==0){
swap(p.first,p.second);
return p;
}
if(t==1){
p.second+=n>>1;
return p;
}
if(t==2){
p.first+=n>>1;
p.second+=n>>1;
return p;
}
if(t==3){
swap(p.first,p.second);
p.first=n-1-p.first;
p.second=(n>>1)-1-p.second;
return p;
}
}
inline void solve(){
int n,k;
cin>>n>>k;
pair<int,int> ans=dfs(n,k-1);
cout<<ans.first+1<<' '<<ans.second+1<<'\n';
}
int main(){
ios_base::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
int T;T=1;
// cin>>T;
for(;T--;)solve();
}
Problem G.Rectilinear Regions
通过队伍数:16/107
题目大意:
给出两条阶梯型的线 \(L,U\),求出那些 \(U\) 在上,\(L\) 在下围成的封闭的多边形的面积的和。
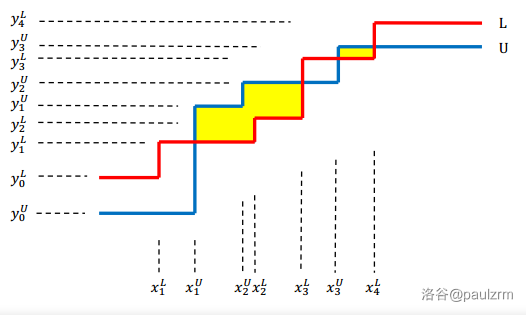
题解:
按照题意尺取法模拟。把一个大块分成一个个矩形求面积之和。
#include<bits/stdc++.h>
#define ll long long
#define mp make_pair
using namespace std;
const int mxn=1e6+6;
struct node{
ll x,y,t;
}p[mxn];
ll n,m,nn,mm,lst=-1,pre,k;
inline bool cmp(node x,node y){return x.x<y.x;}
inline void solve(){
cin>>n>>m;
cin>>nn;for(int i=0;i<n;++i)cin>>p[i].x>>p[i].y,p[i].t=0;
cin>>mm;for(int i=0;i<m;++i)cin>>p[i+n].x>>p[i+n].y,p[i+n].t=1;
sort(p,p+n+m,cmp);
ll ans=0,cnt=0,sum=0;
for(;k<n+m;){
int x=p[k].x;
bool f=0;
if(nn<mm)sum+=(x-pre)*(mm-nn);//求小块矩形面积之和 注意要先加到sum里,因为要求是封闭的多边形 可能最后一段不合上了
else f=1;
for(;k<n+m and p[k].x==x;++k){
if(p[k].t==0)nn=p[k].y;
else mm=p[k].y;
}
if(nn<mm and f)lst=x;
else if(nn>=mm and !f){
if(lst>=0){
++cnt; //同理 因为要求的是封闭多边形
ans+=sum;
}
sum=0;
lst=x;
}
pre=x;
}
cout<<cnt<<' '<<ans<<'\n';
}
int main(){
ios_base::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
int T;T=1;
// cin>>T;
for(;T--;)solve();
}
Problem H.Rock Paper Scissors
通过队伍数:42/107
队友谦虚不会FFT就让我写了orz
题目大意:
有两个人玩石头剪刀布。他们的出法可以用两个字符串表示。每一个字符串的字符都为R P 或 S。显然 R 赢 S,S 赢 P,P 赢 R。
已知第一个人的串长度为 \(n\),第二个人的串为 \(m \le n\)。
现在要从第一个人的串 \(a\) 中选出一个长度为 \(m\) 的子串 \(c\) 与 第二个人的串\(b\) 打。规则是 \(c_i\) 和 \(b_i\) 打 \((1 \le i \le m)\)。可以发现一共有 \(n-m+1\) 种选法。
现在需要最大化第二个人 \((b)\) 赢的局数。输出最多能赢多少局。
题解:
这真的是FFT入门题啊
我们可以先将 \(a\) 中的所有 S -> R,P -> S,R -> P,变为能赢的序列。
然后就是希望最大化 \(b\) 与 \(a\) 的一个子串重合的个数。
这不就是FFT模板了吗
对于 RGB 三种字符,我们分开来讨论:
假设现在考虑到 R:
构造两个多项式 \(F_R\) 和 \(G_R\) 。 如果 \(a_i=R\),那么 \(F_R\) 中第 \(i\) 项的系数就是 \(1\)。反之就是 \(0\)。
\(G_R\) 同理由 \(b\) 得到。
然后将 \(F_R\) 和 \(G_R\) 相乘 得到一个新多项式 \(A_R\)
同理得到 \(A_P\) 和 \(A_S\)
然后我们将 \(A_R\),\(A_P\) 和 \(A_S\) 相加得到 \(T\)。
我们对 \(T\) 的 \(m+1\) 项开始一直到 \(n+m\) 项取 \(max\) 即可。(因为需要全部匹配上)
#include<bits/stdc++.h>
#define ll long long
#define reg register
#define mp make_pair
#define ri register int
#define ld double
using namespace std;
const int mxn=6e5+5;
const ld PI=acos(-1);
int n,m,k,sm;
int rev[mxn];
complex<ld>F1[mxn],G1[mxn],F2[mxn],G2[mxn],F3[mxn],G3[mxn];
int A1[mxn],A2[mxn],A3[mxn];
inline void makerev(int N){
ri d=N>>1,p=0;
rev[p++]=0,rev[p++]=d;
for(int w=2;w<=N;w<<=1){
d>>=1;
for(ri t=0;t<w;++t)rev[p++]=rev[t]|d;
}
}
inline void FFT(complex<ld>*A,int N){ //FFT板子
for(ri i=1;i<N;++i)if(rev[i]>i)swap(A[rev[i]],A[i]);
for(ri len=2,M=1;len<=N;M=len,len<<=1){
complex<ld>W(cos(PI/M),sin(PI/M)),w(1.0,0.0);
for(ld L=0,R=len-1;R<=N;L+=len,R+=len){
complex<ld>w0=w;
for(int p=L,lim=L+M;p<lim;++p){
complex<ld> x=A[p]+w0*A[p+M],y=A[p]-w0*A[p+M];
A[p]=x,A[p+M]=y;
w0*=W;
}
}
}
}
string a,b;
int main(){
ios_base::sync_with_stdio(false);
cin>>n>>m>>a>>b;
reverse(b.begin(),b.end());
for(int i=0;i<n;++i){
if(a[i]=='R')a[i]='P';
else if(a[i]=='P')a[i]='S';
else if(a[i]=='S')a[i]='R';
}
sm=n+m;k=1;
for(;k<=sm;)k<<=1;
makerev(k);
//R
for(int i=0;i<n;++i)if(a[i]=='R')F1[i]=1;
for(int i=0;i<m;++i)if(b[i]=='R')G1[i]=1;
FFT(F1,k);
FFT(G1,k);
for(int i=0;i<k;++i)F1[i]*=G1[i];
FFT(F1,k);
reverse(F1+1,F1+k);
for(int i=0;i<=sm;++i)A1[i]=(int)(F1[i].real()/(ld)(k)+0.5);
//P
for(int i=0;i<n;++i)if(a[i]=='P')F2[i]=1;
for(int i=0;i<m;++i)if(b[i]=='P')G2[i]=1;
FFT(F2,k);
FFT(G2,k);
for(int i=0;i<k;++i)F2[i]*=G2[i];
FFT(F2,k);
reverse(F2+1,F2+k);
for(int i=0;i<=sm;++i)A2[i]=(int)(F2[i].real()/(ld)(k)+0.5);
//S
for(int i=0;i<n;++i)if(a[i]=='S')F3[i]=1;
for(int i=0;i<m;++i)if(b[i]=='S')G3[i]=1;
FFT(F3,k);
FFT(G3,k);
for(int i=0;i<k;++i)F3[i]*=G3[i];
FFT(F3,k);
reverse(F3+1,F3+k);
for(int i=0;i<=sm;++i)A3[i]=(int)(F3[i].real()/(ld)(k)+0.5);
//sum
int ans=0;
// for(int i=0;i<=sm;++i)cerr<<A1[i]+A2[i]+A3[i]<<' ';cerr<<'\n';
for(int i=m-1;i<=sm;++i)ans=max(ans,A1[i]+A2[i]+A3[i]);
cout<<ans<<'\n';
return 0;
}
Problem I.Slot Machines
通过队伍数:49/107
题目大意:
给你一个长度为 \(n\) 的数组 \(a\)。
你需要找到一对 \(k,p\)(下标从 \(1\) 开始),满足 \(a_{k+1}\dots a_n\) 满足 \(p\) 个一循环(最后一轮可以不满)。
现在需要 \(p\) 最小。在 \(p\) 最小的前提下使得 \(k\) 最小。
题解:
我们知道有个东西叫做 \(kmp\)
它是干什么用的?
求 \(border\):
定义一个字符串 \(s\) 的 \(border\) 为 \(s\) 的一个非 \(s\) 本身的子串 \(t\),满足 \(t\) 既是 \(s\) 的前缀,又是 \(s\) 的后缀。
然后题目怎么转化到这玩意上来?
翻转。
我们可以把数组 \(a\) 转过来。
然后就是前缀重复了。
接着随便搞搞就行了。
#include<bits/stdc++.h>
#define ll long long
#define mp make_pair
using namespace std;
const int mxn=1e6+6;
int a[mxn],nxt[mxn],n;
inline void kmp(){
nxt[0]=-1;
for(int i=0,j=-1;i<=n;){
if(j==-1 or a[i]==a[j])nxt[++i]=++j;
else j=nxt[j];
}
}
inline void solve(){
cin>>n;
for(int i=0;i<n;++i)cin>>a[i];
reverse(a,a+n);//很显然后面的一定呈循环状 倒过来处理就很方便
kmp();
int ak=n-1,ap=1;
for(int i=0;i<=n;++i){ //枚举k
int tp=i-nxt[i],tk=n-i;
if(tp+tk<ak+ap)ak=tk,ap=tp;
else if(tp+tk==ap+ak and tp<ap)ap=tp;
}
cout<<ak<<' '<<ap<<'\n';
}
int main(){
ios_base::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
int T;T=1;
// cin>>T;
for(;T--;)solve();
}
Problem J.Strongly Matchable
通过队伍数:10/107
题目大意:
给你一张 \(n \le 100\) 个点的无向图,保证 \(n\) 为偶数。
定义一种染色方案为,从中任意选出 \(\frac{n}{2}\) 个点染黑,另外 \(\frac{n}{2}\) 个点染白。
定义一个图是“强完美匹配的”,当且仅当,对于所有的染色方案,白点集和黑点集都存在完美匹配。
你需要求出给你的这张图是不是“强完美匹配的”。
题解:
霍尔定理:对于黑点集的所有子集 \(U\),存在完美匹配的条件是它的邻集 \(\delta(U)\) 中的白点数量要 \(\geq |U|\)
由于要求任意染色都满足要求,所以我们直接考虑最坏情况:
对于一个黑点子集 \(U\),剩下的所有黑点都在 \(\delta(U)\) 中。
那么 \(\delta(U)\) 中的白点数量就是 \(|\delta(U)|-(\frac{n}{2}-|U|)\)
所以不合法的情况就是 \(|\delta(U)|-(\frac{n}{2}-|U|) < |U|\)
\(|\delta(U)|-\frac{n}{2}<|U|-|U|\)
得到 \(|\delta(U)|<\frac{n}{2}\)
接下来就套路了?
设原点集为 \(V\)
令 \(U'\) 为 $V \backslash U \backslash \delta(U) $
这个 \(\delta(U)\) 就相当于 \(U\) 和 \(U'\) 的点割。
于是我们就可以对原图中于任意两个点 \(x\) 和 \(y\),以 \(x\) 为源点,\(y\) 为汇点,跑一遍最小点割,如果 $ < \frac{n}{2}$ 就是无解。
附:实际代码在比赛时 TLE 了一次,但神仙队友加了个随机化(对于每个源点随机只跑 \(10\) 个汇点)就 AC 了/bx/bx/bx
Code by 神仙队友 miao22:
#include<bits/stdc++.h>
using namespace std;
const int MAX_V=203,INF=19260817;
struct edge{
int to,cap,rev;
};
vector<edge> G[MAX_V];
int dist[MAX_V],prevv[MAX_V],preve[MAX_V],V;
void add_edge(int from,int to,int cap){
G[from].push_back((edge){to,cap,G[to].size()});
G[to].push_back((edge){from,0,G[from].size()-1});
}
void add_edge2(int from,int to,int cap){
G[from].push_back((edge){to,cap,G[to].size()});
G[to].push_back((edge){from,cap,G[from].size()-1});
}
void init(){
for(int i=0;i<V;i++)G[i].clear();
}
int q[MAX_V];
int max_flow(int s,int t){
int res=0;
while(1){
for(int i=0;i<V;i++)dist[i]=19260817;
dist[s]=0;
int nws=0,nwt=0;q[0]=s;
while(nws<=nwt){
int nw=q[nws++];
for(int i=0;i<G[nw].size();i++)
if(G[nw][i].cap&&dist[G[nw][i].to]==19260817){
dist[G[nw][i].to]=dist[nw]+1;
q[++nwt]=G[nw][i].to;
prevv[q[nwt]]=nw;
preve[q[nwt]]=i;
}
}
if(dist[t]==INF)
return res;
int d=19260817;
for(int v=t;v!=s;v=prevv[v])
d=min(d,G[prevv[v]][preve[v]].cap);
res+=d;
for(int v=t;v!=s;v=prevv[v]){
edge &e=G[prevv[v]][preve[v]];
e.cap-=d;
G[v][e.rev].cap+=d;
}
}
}int n,m,a[5053],b[5053];
int main(){
cin>>n>>m;
for(int i=0;i<m;i++){
scanf("%d%d",a+i,b+i);
a[i]--;b[i]--;
}V=2*n;
srand(time(NULL));
for(int i=0;i<n;i++){
int j,cnt=10;
while(cnt--){
j=rand()%(n-i)+i;
init();
for(int k=0;k<n;k++)
add_edge(k,k+n,1);
for(int k=0;k<m;k++){
add_edge(a[k]+n,b[k],233);
add_edge(b[k]+n,a[k],233);
}
if(max_flow(i+n,j)<n/2){
cout<<-1;
return 0;
}
}
}cout<<1;
}
Problem K.Untangling Chain
通过队伍数:36/107
题目大意:
在二维平面上,从 \((0,0)\) 出发(开始时向右走),向前走一段距离(整数),然后向左转或向右转,重复若干次。给出路径,你需要改变每一次走的距离(不能改变转向),使得路径不相交。
你还需要输出一种方案。
题解:
神仙队友:这是诈骗题,秒了! $\ \ \ \ \ \ \ \ \ $ orz
的确挺诈骗的
他只是说要不相交,没有要求改动最小
所以我们可以尝试螺旋走位。
记录当前的\(x_{min},y_{min},x_{max},y_{max}\),然后走到 \(x_{min}-1,y_{min}-1,x_{max}+1,y_{max}+1\)即可。
Code by miao22:
#include<bits/stdc++.h>
using namespace std;
char c[4]={'R','U','L','D'};
int x[2],y[2],nwx,nwy,n,pt;
int main(){
cin>>n;
while(n--){
int tmp;cin>>tmp>>tmp;
if(c[pt]=='U'){
cout<<y[1]+1-nwy<<' ';
nwy=y[1]+1;
y[1]=nwy;
}
if(c[pt]=='L'){
cout<<nwx-x[0]+1<<' ';
nwx=x[0]-1;
x[0]=nwx;
}
if(c[pt]=='D'){
cout<<nwy-y[0]+1<<' ';
nwy=y[0]-1;
y[0]=nwy;
}
if(c[pt]=='R'){
cout<<x[1]+1-nwx<<' ';
nwx=x[1]+1;
x[1]=nwx;
}
pt=(pt+tmp+4)%4;
}
}
Problem L.Vacation Plans
通过队伍数:14/107
题目大意:
有 \(n\le 3\) 张带权有向图(不是同一张图),每张图的起点都是 \(1\),终点为 \(to_i \ (1 \le i \le n)\)。第 \(i\) 张图的节点数 \(c_i \le 50\)。
有 \(n\) 个人。第 \(i\) 个人在第 \(i\) 个图上。所有人同时出发,要求同时结束。
假设当前一个人在\(u\)。每一次可以沿着一条 \(\{u_i,v_i,w_i\}\) 的边(从\(u_i\) 走到 \(v_i\) 代价 \(w_i\)) 走到 \(v_i\),或者花费 \(t_u\) 的代价留在原地,均花费时间 \(1\)。
问你最小的代价使得在所有人同时出发的前提下同时到达终点。
题解:
留在原地相当于连一条 \(\{i,i,t_i\}\) 的边。
按照时间分层dp。
我们对每个图分开来考虑。
令 \(dp_{g,t,i}\) 表示在第 \(g\) 张图,经过了 \(t\) 份时间,走到了 \(i\) 号节点的最小代价。
按照拓扑序直接暴力转移即可。
然后统计答案。
枚举一个同时到达终点的时间 \(d\)。可以感性证明 \(d \le \prod\limits_{i=1}^{n}v_i \le 50^3=125000\)
这一时刻的答案就是 \(\sum\limits_{i=1}^{n} dp_{i,d,to_g}\)
#include<bits/stdc++.h>
#define ll long long
#define mp make_pair
using namespace std;
#define int ll
const int mxn=55;
const int lim=mxn*mxn*mxn;
struct graph{
vector<pair<int,ll> >g[mxn];
ll dp[lim][mxn],n,m,to;
inline void read(){
cin>>n>>m;
memset(g,0,sizeof(g));
for(int i=1,w;i<=n;++i)cin>>w,g[i].push_back(mp(i,w));
for(int i=1,u,v;i<=m;++i){
ll w;
cin>>u>>v>>w;
g[u].push_back(mp(v,w));
}
cin>>to;
}
inline void go(){
for(int i=0;i<lim;++i)for(int j=0;j<=n;++j)dp[i][j]=1145141919810;
dp[0][1]=0;
for(int t=0;t<lim;++t)for(int i=1;i<=n;++i)for(pair<int,ll>p:g[i])dp[t+1][p.first]=min(dp[t+1][p.first],dp[t][i]+p.second);
}
inline ll get(int x){return dp[x][to];}
}G[4];
inline void solve(){
int cc;cin>>cc;
for(int i=1;i<=cc;++i)G[i].read(),G[i].go();
ll ans=1145141919810;
for(int t=0;t<lim;++t){
ll tmp=0;
for(int i=1;i<=cc;++i)tmp+=G[i].get(t);
ans=min(ans,tmp);
}
cout<<ans<<'\n';
}
signed main(){
ios_base::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
int T;T=1;
// cin>>T;
for(;T--;)solve();
return 0;
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号