分治递归

• 分治

分治，就是分而治之，也就是将大问题分成多个子问题，再由子问题分成更小子问题，直到可以直接得到答案，再由当前的问题返回给上一个子问题

 

 

• 归并排序

归并排序思路：先分再合，每次找到数组的中间值，然后分成左右两遍排序，不断分成两部分，直到每部分只剩下一个数，然后将数组合并成有序的

 

 

P1908 逆序对

题目描述

猫猫 TOM 和小老鼠 JERRY 最近又较量上了，但是毕竟都是成年人，他们已经不喜欢再玩那种你追我赶的游戏，现在他们喜欢玩统计。

最近，TOM 老猫查阅到一个人类称之为“逆序对”的东西，这东西是这样定义的：对于给定的一段正整数序列，逆序对就是序列中 a_i>a_jai​>aj​ 且 i<ji<j 的有序对。知道这概念后，他们就比赛谁先算出给定的一段正整数序列中逆序对的数目。注意序列中可能有重复数字。

Update:数据已加强。

输入格式

第一行，一个数 nn，表示序列中有 nn个数。

第二行 nn 个数，表示给定的序列。序列中每个数字不超过 10^9109。

输出格式

输出序列中逆序对的数目。

输入输出样例

输入 #1复制

6
5 4 2 6 3 1

输出 #1复制

11

说明/提示

对于 25\%25% 的数据，n \leq 2500n≤2500

对于 50\%50% 的数据，n \leq 4 \times 10^4n≤4×104。

对于所有数据，n \leq 5 \times 10^5n≤5×105

请使用较快的输入输出

应该不会 O(n^2)O(n2) 过 50 万吧 by chen_zhe

解析

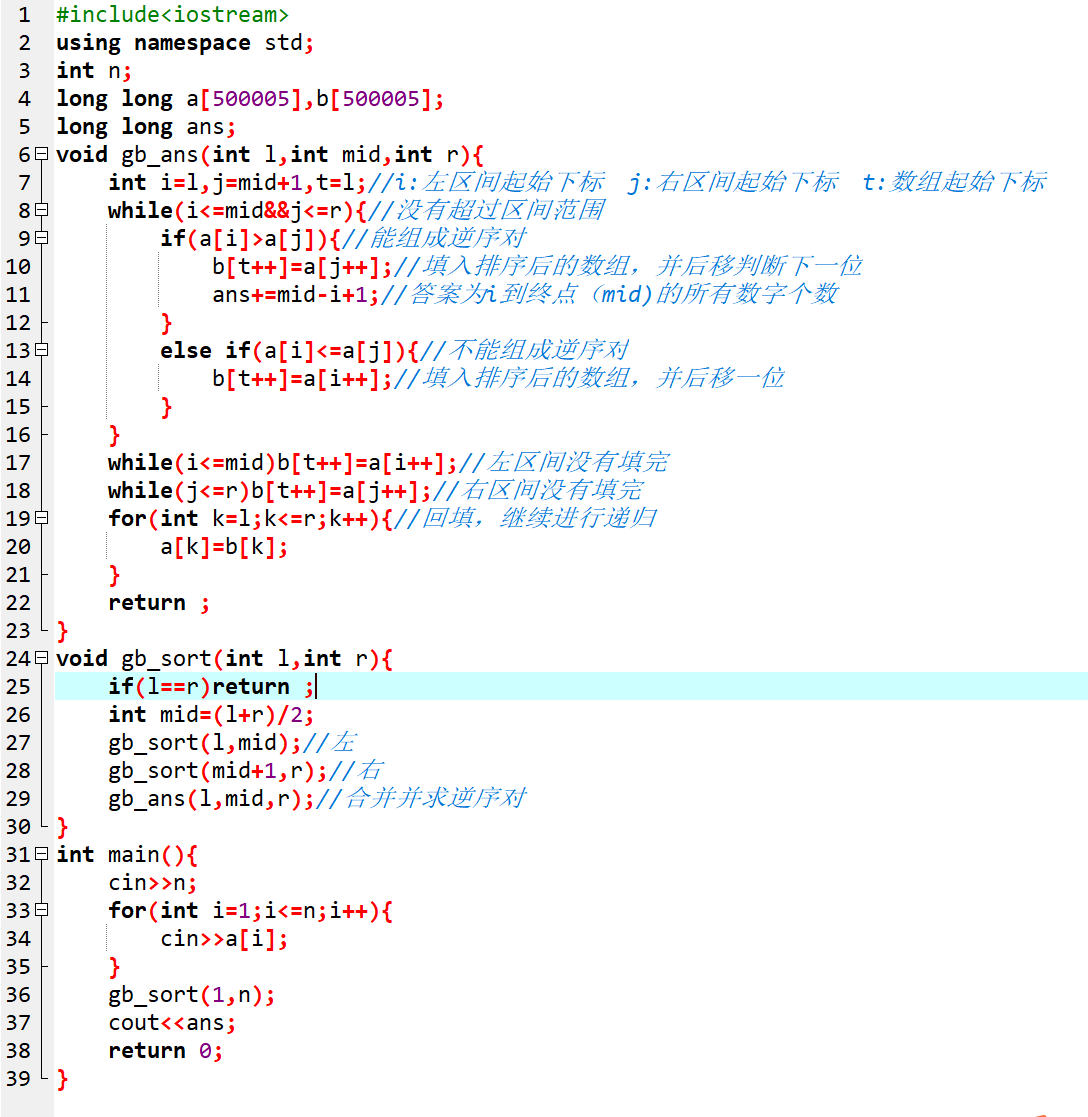
本题采用归并排序求解

 

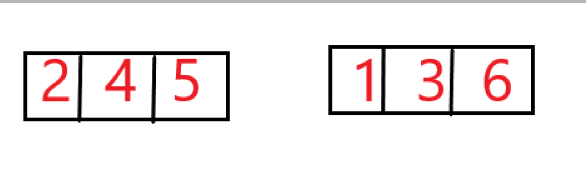
列如上图两个有序的数组

可以想象有两个“指针”

i为第一个序列当前指向的元素下标

j为第二个序列当前指向的元素下标

n为两个序列长度

初始i=1,j=1

先看1的逆序对：

当a[i]>b[j]则（a[i],b[j]）为一对逆序对，因为当前序列是按升序排列所以第一个数组从i到n都与b[j]是逆序对

所以1的逆序对有（2,1）（4,1）（5,1）

b[j]的逆序对求完，j++（往后移动）

再看3的逆序对：

       此时a[i]<b[j],则将i向后移，直到找到比b[j]大的数

       3的逆序对有（4,3）（5,3）

以此类推……

代码