字符串（2） Trie/01-Trie

感觉就是一个可拓展性很弱的数据结构

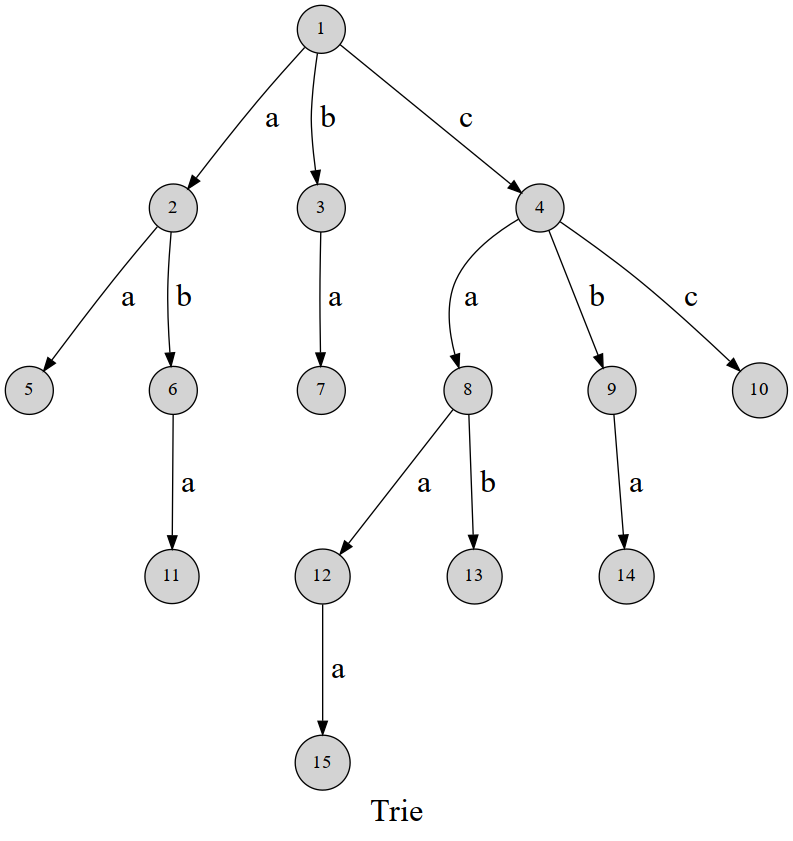
先放一张图：

Trie / 01-Trie

基本结构

Trie 树，又称字典树，是一个以边来存储信息的数据结构，每条边代表了一种字符。通过观察上图可以发现，从根节点往下遍历可以拼出一个完整的字符串。

在实际实现中，我们对于每个点存下他们的子节点，该点到每个子节点边储存着信息。（比如上图中 \(t_{1,1} = 2\)，即节点 \(1\) 向下连边为 \(a\) 的子节点是节点 \(2\)）对于某个节点，我们需要记录下是否有字符串在当前位置结束。

实现还是相当好实现的。

01-Trie 其实是 Trie 的一个变种，它的边储存信息不再是字符，而是数字在二进制下某位，我们从上可以对整数进行二进制分解，然后将其加入 01-Trie。注意到，我们可以分不同情况决定是从高位到低位进行插入或是从低位到高位。

实际应用

其实这个东西的应用整体上就分为三类：检索字符串；判断前后缀；求最大或最小异或和。

检索字符串：

我们可以通过字典树来判断字符串，通过从上往下查找以及判断字符串结尾判断一个字符串是否在查找前出现过。

判断前后缀：

对于字符串从前往后加入字典树的这种方法来说，我们可以通过从上往下查找这条路径上的节点是否都被开通来判断该前缀是否出现过。对于后缀来说同理可得。

求最大或最小异或对：

对于求取最大异或对，我们可以建立一棵 01-Trie，将每个数进行从高到低位的二进制分解位固定位数（32 或 64）后插入这棵 01-Trie。我们可以贪心的考虑最大异或对，必然在高位上尽可能能做到取反的地方进行取反。我们既可以选择对这棵树进行 DFS 统计答案，也可以选择对于每个数在 01-Trie 上 \(O(\log n)\) 的查找与它异或和最大的数和异或和。

对于求取最小异或对，我们可以参考最大异或对，只是每次想取反这一思想变为了每次想取相同。

建立平衡树

要素

我们考虑将边上的信息下方的该边所连的子节点中，我们可以注意到以下两点：

• 01-Trie的本质是一棵二叉树。

• 从根节点开始的路径左儿子的值总是小于右儿子。

我们就可以根据这两点建立平衡树了。

建立

对于每个节点，我们需要维护：该节点的左右儿子、二进制分解后经过这个节点的数的数量（\(siz\)）。

（看了几篇，发现他们都不约而同的维护了以该节点结尾的数的数量（\(cnt\)），但是我们在进行固定位数的拆分后，显然叶子节点的深度是一定的，所以对于非叶子节点 \(cnt_i\) 为 0，对于叶子节点 \(cnt_i = siz_i\)，发现维护这玩意还不如维护该位置是否是叶子节点，但是我们只会在从根节点向下遍历时用到叶子节点，而树高一定，所以维护该位置是否时叶子节点也是没有意义的 ，就很抽象 ）

插入/删除：正常 01-Trie 的插入即可。删除与插入操作相同，路径上每个点的 \(siz_i\) 减一即可。

查找 x 的排名：从根节点开始往下，如果当前数的当前二进制位为 1，就把排名加上它的左子树的值。

查找排名为 x 的值：考虑一个和线段树二分很像的操作，如果左子树的 \(siz_i\) 大了，则答案在左子树，否则答案在右子树。

查找 x 的前驱：查出来 x 的位置然后找位置减一的数即可。

查找 x 的后缀：查找 \(x+1\) 的位置，然后找数即可。（一定是这样，不然会被神秘数据卡掉）

Code.

#include<bits/stdc++.h>
#define endl "\n"
#define pb push_back
#define mkp make_pair
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
//value 
const int inf=2147483647;
const int mod=1e9+7;
const int high=25;
const int N=1e5+5;
const int M=1e7+2;
int t[N*(high+1)][2],siz[N*(high+1)],tot;



//function 
void solve(){
	
	
	
	return;
}
void add(int x,int k){
	int tmp1=0;
	for(int i=high;i>=0;i--){
		int tmp2=(x&(1<<i));
		if(tmp2!=0)tmp2=1;
		if(t[tmp1][tmp2]==0)t[tmp1][tmp2]=++tot;
		tmp1=t[tmp1][tmp2];
		siz[tmp1]+=k;
	}
}
int get_rank(int x){
	int tmp1=0,ans=1;
	for(int i=high;i>=0;i--){
		int tmp2=(x&(1<<i));
		if(tmp2!=0)tmp2=1;
		if(tmp2==1 && t[tmp1][0])ans+=siz[t[tmp1][0]];
		tmp1=t[tmp1][tmp2];
		if(tmp1==0)break;
	}
	return ans;
}
int get_kth(int x){
	int tmp1=0,ans=0;
	for(int i=high;i>=0;i--){
		int s=siz[t[tmp1][0]];
		if(x>s){
			ans+=(1<<i);
			x-=s;
			tmp1=t[tmp1][1];
		}
		else tmp1=t[tmp1][0];
		if(tmp1==0)break;
	}
	return ans;
}
int pre(int x){
	return get_kth(get_rank(x)-1);
}
int nxt(int x){
	return get_kth(get_rank(x+1));
}


 
int main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0); 
	
//	freopen(".in","r",stdin);
//	freopen(".out","w",stdout);
	
	int n;
	cin>>n;
	for(int i=1;i<=n;i++){
		int opt,x;
		cin>>opt>>x;
		if(opt==1)add(x+M,1);
		else if(opt==2)add(x+M,-1);
		else if(opt==3)cout<<get_rank(x+M)<<endl;
		else if(opt==4)cout<<get_kth(x)-M<<endl;
		else if(opt==5)cout<<pre(x+M)-M<<endl;
		else if(opt==6)cout<<nxt(x+M)-M<<endl;
	}
	
	
	
	return 0;
}