图论(7) 树链剖分
调了一晚上才过,也是没救了。
定义
事实上,树链剖分只是一个统称,在实际应用时,我们常常使用重链剖分(还有长链剖分)。
我们通常使用重链剖分维护一下几种操作:
-
修改 树上两点之间的路径上 所有点的值。
-
查询 树上两点之间的路径上 节点权值的 和/极值/其它(在序列上可以用数据结构维护,便于合并的信息)。
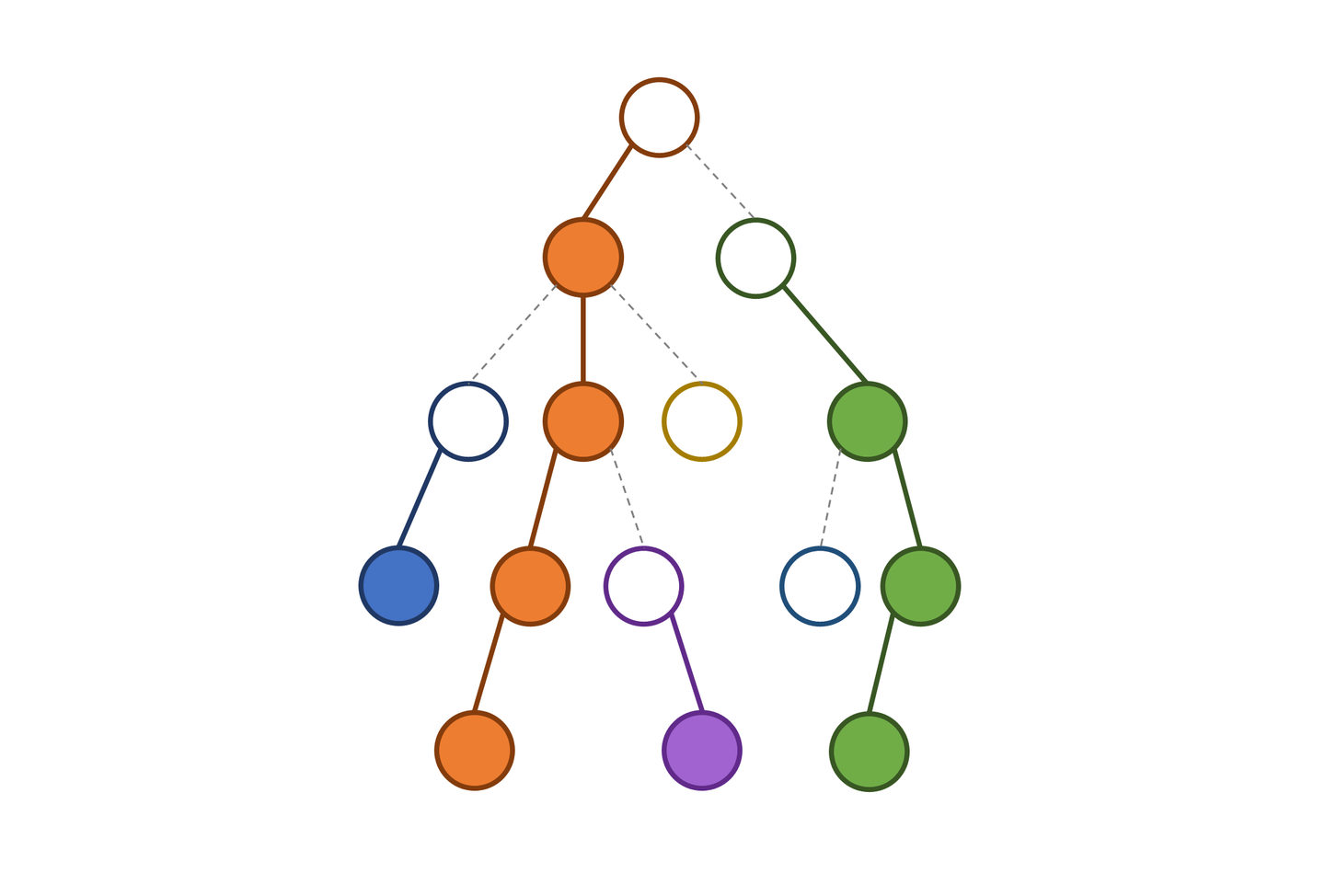
在这里我们给出一下定义:
-
定义 重儿子 表示其子节点中子树最大的子结点。如果有多个子树最大的子结点,取其一。如果没有子节点,就无重子节点。
-
定义 轻儿子 表示剩余的所有子结点。
-
从这个结点到重子节点的边为 重边。
-
到其他轻子节点的边为 轻边。
-
若干条首尾衔接的重边构成 重链。
重链剖分即将一个树型结构拆分成一个线性结构,以便使用数据结构维护。
实现
构建
我们根据定义可以很容易的想到我们可以通过两轮遍历来完成重链剖分:
-
遍历出每个节点的重子节点。
-
从树根开始进行重儿子优先 dfs 序的遍历,构成线性结构。
注意到,由于我们遍历时的顺序是重儿子优先,所以重链的新编号是连续的;由于进行的是 dfs 序的遍历,所以子树的新编号也是连续的。
让我们把以上过程落实到代码上:
void dfs1(ll u,ll fat){
dep[u]=dep[fat]+1;
fa[u]=fat;
siz[u]=1;
ll mson=-1;
for(auto v:g[u]){
if(v==fa[u])continue;
dfs1(v,u);
siz[u]+=siz[v];
if(siz[v]>mson){
mson=siz[v];
son[u]=v;
}
}
}
void dfs2(ll u,ll rot){
id[u]=++tot;
b[tot]=a[u];
top[u]=rot;
if(!son[u])return;
dfs2(son[u],rot);
for(auto v:g[u]){
if(v!=fa[u] && v!=son[u])dfs2(v,v);
}
}
其中 \(dep_i\) 表示 \(i\) 的深度,\(fa_i\) 表示 \(i\) 的父节点,\(siz_i\) 表示以 \(i\) 为根的子树大小,\(son_i\) 表示 \(i\) 的重儿子,\(id_i\) 表示 \(i\) 重链剖分后的新编号,\(b\) 存储着重链剖分后的树的数据,\(top_i\) 表示 \(i\) 所在重链的根节点。
操作
观察我们要完成的操作,我们可以发现用线段树操作比较好。
我们思考如何对一条树链进行操作,首先我们可以将其分为两节点到其 \(lca_{u,v}\)。然后我们注意到一个节点到其祖先节点必然是重链轻链交替的(可以观察图得出),而交替次数不会超过 \(\log n\) 次,所以我们可以得出以下操作:
-
单次对深度更深的节点向上操作整条重链。
-
通过重链祖先跳轻链到另一条重链。
查询思路相似,代码如下:
void change1(ll x,ll y,ll z){
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]])swap(x,y);
change(1,n,id[top[x]],id[x],z,1);
x=fa[top[x]];
}
if(dep[x]>dep[y])swap(x,y);
change(1,n,id[x],id[y],z,1);
}
ll query1(ll x,ll y){
ll res=0;
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]])swap(x,y);
res+=query(1,n,id[top[x]],id[x],1);
res%=mod;
x=fa[top[x]];
}
if(dep[x]>dep[y])swap(x,y);
res+=query(1,n,id[x],id[y],1);
res%=mod;
return res;
}
其中 \(change\) 是线段树的修改操作,\(query\) 是线段树的查询操作。
那么我们其实就可以做树链剖分的模板了。注意到板子中还多了一个对子树节点加的操作,事实上,这个操作等价于对于 \([id_i , id_i + siz_i -1]\) 进行区间加。
以下是全部代码:
Code.
#include<bits/stdc++.h>
#define endl "\n"
#define pb push_back
#define mkp make_pair
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
//value
const int inf=2147483647;
const int N=100005;
ll t[N<<2],tg[N<<2],len[N<<2];//线段树
ll dep[N],fa[N],a[N],b[N],siz[N],id[N],top[N],son[N],tot;
ll n,m,R,mod;
vector<ll>g[N];
//function
void solve(){
return;
}
//__________构建___________
void dfs1(ll u,ll fat){
dep[u]=dep[fat]+1;
fa[u]=fat;
siz[u]=1;
ll mson=-1;
for(auto v:g[u]){
if(v==fa[u])continue;
dfs1(v,u);
siz[u]+=siz[v];
if(siz[v]>mson){
mson=siz[v];
son[u]=v;
}
}
}
void dfs2(ll u,ll rot){
id[u]=++tot;
b[tot]=a[u];
top[u]=rot;
if(!son[u])return;
dfs2(son[u],rot);
for(auto v:g[u]){
if(v!=fa[u] && v!=son[u])dfs2(v,v);
}
}
//__________线段树___________
void atg(ll o,ll w){
t[o]+=len[o]*w;
tg[o]+=w;
}
void push_up(ll o){
t[o]=t[o<<1]+t[o<<1|1];
}
void push_down(ll o){
if(!tg[o])return;
atg(o<<1,tg[o]);
atg(o<<1|1,tg[o]);
tg[o]=0;
}
void build(ll l,ll r,ll o){
len[o]=r-l+1;
if(l==r){
t[o]=b[l];
return;
}
ll mid=(l+r)>>1;
build(l,mid,o<<1);
build(mid+1,r,o<<1|1);
push_up(o);
}
void change(ll l,ll r,ll L,ll R,ll w,ll o){
if(l>=L && r<=R)atg(o,w);
else {
push_down(o);
ll mid=(l+r)>>1;
if(L<=mid)change(l,mid,L,R,w,o<<1);
if(R>mid)change(mid+1,r,L,R,w,o<<1|1);
push_up(o);
}
}
ll query(ll l,ll r,ll L,ll R,ll o){
if(l>=L && r<=R)return t[o];
push_down(o);
ll res=0,mid=(l+r)>>1;
if(mid>=L)res+=query(l,mid,L,R,o<<1);
if(mid<R)res+=query(mid+1,r,L,R,o<<1|1);
return res;
}
//__________操作___________
void change1(ll x,ll y,ll z){
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]])swap(x,y);
change(1,n,id[top[x]],id[x],z,1);
x=fa[top[x]];
}
if(dep[x]>dep[y])swap(x,y);
change(1,n,id[x],id[y],z,1);
}
ll query1(ll x,ll y){
ll res=0;
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]])swap(x,y);
res+=query(1,n,id[top[x]],id[x],1);
res%=mod;
x=fa[top[x]];
}
if(dep[x]>dep[y])swap(x,y);
res+=query(1,n,id[x],id[y],1);
res%=mod;
return res;
}
void change2(ll x,ll z){
change(1,n,id[x],id[x]+siz[x]-1,z,1);
}
ll query2(ll x){
return query(1,n,id[x],id[x]+siz[x]-1,1)%mod;
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
cin>>n>>m>>R>>mod;
for(int i=1;i<=n;i++)cin>>a[i];
for(int i=1;i<=n-1;i++){
ll u,v;
cin>>u>>v;
g[u].push_back(v);
g[v].push_back(u);
}
dep[R]=1;
dfs1(R,0);
dfs2(R,R);
//重链剖分后的序列位于b
build(1,n,1);
while(m--){
ll opt;
cin>>opt;
if(opt==1){
ll x,y,z;
cin>>x>>y>>z;
z%=mod;
change1(x,y,z);
}
else if(opt==2){
ll x,y;
cin>>x>>y;
cout<<query1(x,y)<<endl;
}
else if(opt==3){
ll x,z;
cin>>x>>z;
change2(x,z);
}
else{
ll x;
cin>>x;
cout<<query2(x)<<endl;
}
}
return 0;
}
应用
关于重链剖分的主要应用其实在维护树上路径信息和维护子树信息,当然也可用于求最近公共祖先。主要创新点其实在树剖后的数据结构上。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号