数据结构（2） 并查集

并查集

并查集基础

并查集是一个用于维护元素所属集合的一种数据结构，真实实现为使用一个指针指向另一个（或自身）所属在的同一集合中的元素，构成一个森林。基础操作共有两种：合并和查询。

合并：合并两个集合时，我们通常通过并查集找到某一集合中的树根，将其连接到另一棵树上。

查询：利用并查集查找两者所在集合的根节点是否为同一个。若是，则两点在同一集合；如不是，则两点在不同集合。

我们注意到，当整个树林构成一条链时，单次查询的时间复杂度会达到 \(O(n)\)，这是很劣的，所以我们考虑优化：

1. 路径压缩：当我们只关心集合中的元素而并不关心其从属关系时，我们可以选择将集合中的所有元素都连接到同一个节点上。时间复杂度趋近于 \(O(1)\)。（仅为趋近）

2. 启发式合并：如果我们希望保留元素间的从属关系时，我们可以在合并的时候选择将元素数少或深度小的集合连向更大的集合的根节点。时间复杂度约为 \(\alpha(n))\)。

关于阿克曼函数的反函数，详见并查集复杂度。

Code.

#include<bits/stdc++.h>
#define endl "\n"
using namespace std;
typedef long long ll;

int fa[200005];

int find(int a){
	if(a==fa[a])return a;
	return fa[a]=find(fa[a]);
}

int main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0); 
	
	int n,m;
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		fa[i]=i;
	}
	for(int i=0;i<m;i++){
		int tmp,x,y;
		cin>>tmp>>x>>y;
		if(tmp==1){
			fa[find(x)]=find(y);
		}
		else if(tmp==2){
			if(find(x)==find(y)) cout<<"Y"<<endl;
			else cout<<"N"<<endl;
		}
	}
	
	return 0;
}

并查集技巧

拓展域并查集

具体使用情景：P1892 [BalticOI 2003] 团伙。

注意到我们可以很容易用并查集的处理朋友关系，但我们似乎没有办法解决敌人关系。

这时候就可以使用拓展域并查集了，拓展域并查集适于解决多种关系或给定关系但双方都不确定的问题。具体是将原点拆分成多个点，构成多个集合，以维护不同的关系。

以这题为例，我们可以将点一分为二，构成两个集合，朋友关系就将第一个集合中的元素连接起来，敌人就将第一个集合与第二个集合中的元素连接起来。

有点奇怪，但原理实际上和反集有关，我们新建的集合维护的其实是朋友和朋友的中间态，即题目中所说的“敌人的敌人是朋友”，我们用第二个集合将因为敌人关系而导致的朋友间接的连接了起来。

Code.

#include<bits/stdc++.h>
#define endl "\n"
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
//value 
int fa[2050];
int cnt[1005];

//function 
int root(int x){
	if(fa[x]==x)return x;
	return fa[x]=root(fa[x]);
}
int main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0); 
	
	int n,m;
	cin>>n>>m;
	for(int i=0;i<2050;i++){
		fa[i]=i;
	}
	for(int i=0;i<m;i++){
		char e;
		int q,w;
		cin>>e;
		cin>>q>>w;
		if(e=='F')fa[root(q)]=root(w);
		else {
			fa[root(w+n)]=root(q);
			fa[root(q+n)]=root(w);
		}
	}
	/*
	int ans=0;
	for(int i=1;i<=n;i++){
		if(fa[i]==i)ans++;
	}
	cout<<ans<<endl;
	*/	
	int ans=0;
	for(int i=1;i<=n;i++)cnt[root(i)]++;
	for(int i=1;i<=n;i++)if(cnt[i]!=0)ans++;
	cout<<ans<<endl;
	
	
	return 0;
}

拓展域并查集还有一个非常有意思的应用：拓展域并查集判二分图。

由于二分图的充要条件是图中不存在奇环，我们可以建一个包含两个集合的拓展域并查集，每次连边时将第一个集合中的点和第二个集合中的点连起来，即 \(merge(u,n+v)\) 和 \(merge(v,n+u)\)，如果新增一条边时存在了奇环，则会有某个点出现 \(find(p)==find(n+p)\) 的情况，因此我们可以用拓展域并查集可以判断二分图。

让我们思考为什么存在奇环会出现 \(find(p)==find(n+p)\) 的情况：

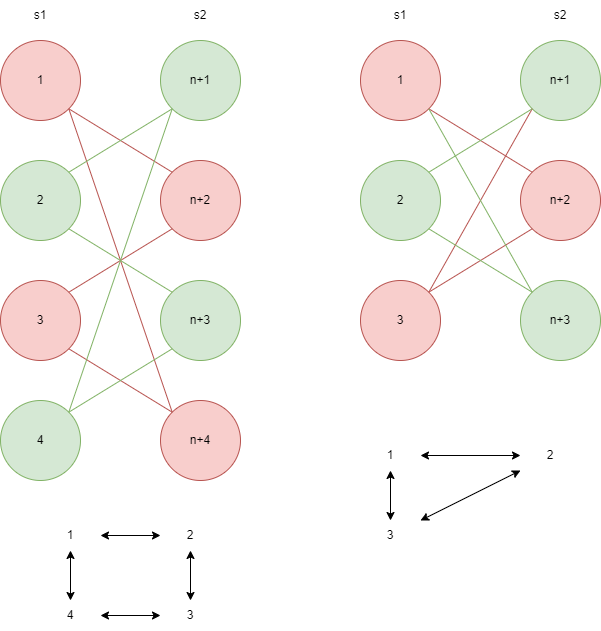
从这个图上就可以观察的很清楚，左图中绿色和红色构成了两个集合，而右图中全部元素都混在了同一个集合。

虽然好像还是没有解释为什么

带权并查集

具体使用情景：P1196 [NOI2002] 银河英雄传说

注意到我们可以很容易的维护两人是否在同一队列，但是我们似乎没有办法解决他们在队列里差了中间几个人。

这时候就可以使用带权并查集了，带权并查集适用于两元素之间的关系带一个或多个权值的情况。本题的应用比较简单，在未进行路径压缩时边权为 \(1\)，路径压缩时可根据父节点的边权进行转移。

Code.

#include<bits/stdc++.h>
#define endl "\n"
#define pb push_back
#define mkp make_pair
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
//value 
const int inf=2147483647;
const int mod=1e9+7;
int a[100005],fa[100005],d[100005],siz[100005];



//function 
void solve(){
	
	
	
	return;
}
int find(int x){
	if(fa[x]==x)return x;
	int tmp=find(fa[x]);
	d[x]+=d[fa[x]];
	return fa[x]=tmp;
}
void change(int x,int y){
	x=find(x);
	y=find(y);
	fa[x]=y;
	d[x]=siz[y];
	siz[y]+=siz[x];
}
void query(int x,int y){
	if(find(x)==find(y))cout<<abs(d[x]-d[y])-1<<endl;
	else cout<<-1<<endl;
}



 
int main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0); 
	
//	freopen(".in","r",stdin);
//	freopen(".out","w",stdout);
	
	int t;
	cin>>t;
	for(int i=1;i<=30000;i++)fa[i]=i;
	for(int i=1;i<=30000;i++)siz[i]=1;
	
	while(t--){
		char c;
		int x,y;
		cin>>c>>x>>y;
		if(c=='M')change(x,y);
		else query(x,y);
	}
	
	
	
	return 0;
}

可撤销并查集

其实就是一个非常简单的东西。

我们考虑将每次进行并查集合并的时候，使用一个栈将操作记录下来，当需要撤销的时候将合并时被修改的点的父节点设为自己即可。注意到我们需要维护这样的一个父子关系，所以我们只能使用按秩合并。