图论(5) 树(直径,中心,重心,LCA)
树
有关树的基本定义一类可以查找 OI Wiki 上树基础。这里不再进行多余赘述,只介绍一些树上问题。(烟都不烟了)
树的直径
定义:树上任意两节点之间最长的简单路径即为树的「直径」。
性质:若树上所有边边权均为正,则树的所有直径中点重合。
两次 dfs
首先介绍一个定理:在一棵树上,从任意节点 \(y\) 开始进行一次 DFS,到达的距离其最远的节点 \(z\) 必为直径的一端。
那么我们根据这一定理可以想到,我们可以从任意一个节点进行 dfs,找到与他距离最远的节点,该节点一定为直径的一端。我们从这一节点再次进行 dfs 可以找到直径的另一端。这样我们就找到了该树的直径。
形式化的表达为:首先从任意节点 \(y\) 开始进行第一次 DFS,到达距离其最远的节点,记为 \(z\),然后再从 \(z\) 开始做第二次 DFS,到达距离 \(z\) 最远的节点,记为 \(z'\),则 \(\delta(z,z')\) 即为树的直径。
Code.
#include<bits/stdc++.h>
#define endl "\n"
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
//value
const int inf=2147483647;
const int mod=1e9+7;
vector<int>e[1000005];
int dis[1000005];
//function
int dfs(int x,int fa){
dis[x]=dis[fa]+1;
int ma=dis[x],ma_id=x;
for(auto i:e[x]){
if(i==fa)continue;
int a=dfs(i,x);
if(dis[a]>ma){
ma=dis[a];
ma_id=a;
}
}
return ma_id;
}
void solve(){
return;
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
int n;
cin>>n;
for(int i=1;i<n;i++){
int u,v;
cin>>u>>v;
e[u].push_back(v);
e[v].push_back(u);
}
dis[0]=-1;
int c=dfs(1,0);
// dis[c]=0;
cout<<dis[dfs(c,0)]<<endl;
return 0;
}
如果想要查找直径上的节点,那么可以在第二轮 dfs 时标记每个节点的父节点,然后从第二轮找到的直径端点开始查找父节点到第一轮找到的直径端点,这样就找出了整条直径。
一次dfs
OI Wiki 上将这种方法归到了树形 DP 中,但是我并不认为在这一解决方法中运用了很多 DP 的思想,而更多的是类似贪心,所以这里将其与树形 DP 区分开来。
对于一个点,如果该点位于直径上,则直径的两个端点即为该点子树中能达到的最深的点与次深的点。(如果直径某一段点深度小于这两点,则显然长度也小于这两点间的简单路径,故不为直径,证明完毕)若该点不位于直径上,则该点子树中能达到的最深的点与次深的点到该点的距离之和,显然小于在直径上的点。故只需要对与每个点找出其子树内所能延伸到的最深点和次深点到该点的距离和,并取最大值即可。
形式化的表达为:我们记录当 \(1\) 为树的根时,每个节点作为子树的根向下,所能延伸的最长路径长度 \(d_1\) 与次长路径(与最长路径无公共边)长度 \(d_2\),那么直径就是对于每一个点,该点 \(d_1 + d_2\) 能取到的值中的最大值。
规定根节点后进行一次 dfs 即可。
Code.
#include<bits/stdc++.h>
#define endl "\n"
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
//value
const int inf=2147483647;
const int mod=1e9+7;
vector<int>e[100005];
int d[100005],d1[100005],d2[100005];
//function
void dfs(int x,int fa){
d1[x]=d2[x]=0;
for(auto i:e[x]){
if(i==fa)continue;
dfs(i,x);
if(d1[i]+1>=d1[x]){
d2[x]=d1[x];
d1[x]=d1[i]+1;
}
else if(d1[i]+1>=d2[x]){
d2[x]=d1[i]+1;
}
}
d[x]=d1[x]+d2[x];
}
void solve(){
return;
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
int n;
cin>>n;
for(int i=1;i<n;i++){
int u,v;
cin>>u>>v;
e[u].push_back(v);
e[v].push_back(u);
}
dfs(1,0);
int ans=0;
for(int i=1;i<=n;i++)ans=max(ans,d[i]);
cout<<ans<<endl;
return 0;
}
如果需要求出一条直径上所有的节点,则可以在 DP 的过程中,记录下每个节点所对应两节点(而不只是记录到该节点的距离),同时记录每个节点在遍历中的父节点。从直径的两个端点向上跳至该节点,将两段序列合并即可。
树形 DP
我们定义 \(dp[u]\):以 \(u\) 为根的子树中,从 \(u\) 出发的最长路径。那么容易得出转移方程:\(dp[u] = \max(dp[u], dp[v] + w(u, v))\),其中的 \(v\) 为 \(u\) 的子节点,\(w(u, v)\) 表示所经过边的权重。
对于树的直径,实际上是可以通过枚举从某个节点出发不同的两条路径相加的最大值求出。因此,在 DP 求解的过程中,我们只需要在更新 \(dp[u]\) 之前,计算 \(d = \max(d, dp[u] + dp[v] + w(u, v))\) 即可算出直径 \(d\)。
我是DP弱手
树的中心
定义:如果节点 \(x\) 作为根节点时,从 \(x\) 出发的最长链最短,那么称 \(x\) 为这棵树的中心。
性质:
-
树的中心一定位于树的直径上。
-
树上所有点到其最远点的路径一定交会于树的中心。
-
当树的中心为根节点时,其到达直径端点的两条链分别为最长链和次长链。
-
当通过在两棵树间连一条边以合并为一棵树时,连接两棵树的中心可以使新树的直径最小。
由定义可得,以树的中心为根的树最大深度最小。由最后一条性质可以想到在直径上找中点,该点即为树的中心。
不知道为什么,树的中心在 OI 中的实际应用好像比较少,明明是个很优雅的东西,例题也没有,模板也没有,就很抽象。
树的重心
定义:如果删除该节点所得子树,子树节点数最大值最小,则该节点为树的重心。
性质:
-
把两棵树通过一条边相连得到一棵新的树,那么新的树的重心在连接原来两棵树的重心的路径上。
-
树中所有点到某个点的距离和中,到重心的距离和是最小的;如果有两个重心,那么到它们的距离和一样。
-
在一棵树上添加或删除一个叶子,那么它的重心最多只移动一条边的距离。
求法
无根树思路不好做就固定点为根后按有根树思考。我们可以进行一轮 DFS 求出每个点子树节点数的最大值与该点的子节点数。对于每个点,如果该节点不为开始时固定的根节点,则显然该节点在无根树中还有一颗子树大小为总结点数-该点在有根树中的子节点数-该节点。故我们可以利用该方法求出每个节点的最大子树的节点数,遍历取最小即可。
关于带权树的重心(例题):
事实上该题由于数据范围极小枚举做法也可过,但仍存在利用树的重心 \(O(n)\) 复杂度解决本题的方法。
我们发现因为有边权的存在,直接求取树的重心不可行了,于是我们需要换一种思路:任意求出一个点的总距离,用该值进行转移。我们定义 \(f_i\) 表示以 \(i\) 为根节点的总距离,\(size_i\) 表示以 \(i\) 为根的子树大小(节点数),令根节点为 1。
我们可以发现对于每个 \(u\) 可到达的 \(v\) 有 \(f_v = f_u + size_1 - size_v * 2\)。
对于这个式子的解释:\(u\) 相比于 \(v\) 对除 \(u\) 的子树外的节点都远了 1 的深度(\(size_1 - size_v\))又对 \(u\) 的子树进了 1 的深度($ - size_v$)。最后对于 \(f_i\) 取最小值即可。
Code.
#include<bits/stdc++.h>
#define endl "\n"
#define pb push_back
#define mkp make_pair
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
//value
const int inf=2147483647;
const int mod=1e9+7;
vector<int>g[100005];
int f[100005],size[100005],a[100005];
//function
void dfs1(int x,int fa){
size[x]=a[x];
f[x]=0;
for(auto i:g[x]){
if(i==fa)continue;
dfs1(i,x);
size[x]+=size[i];
f[x]+=f[i]+size[i];
}
}
void dfs2(int x,int fa){
for(auto i:g[x]){
if(i==fa)continue;
f[i]=f[x]+size[1]-size[i]*2;
dfs2(i,x);
}
}
void solve(){
return;
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
int n;
cin>>n;
for(int i=1;i<=n;i++){
int s1,s2;
cin>>a[i]>>s1>>s2;
if(s1!=0){
g[i].pb(s1);
g[s1].pb(i);
}
if(s2!=0){
g[i].pb(s2);
g[s2].pb(i);
}
}
dfs1(1,0);
dfs2(1,0);
int ans=inf;
for(int i=1;i<=n;i++)ans=min(ans,f[i]);
// for(int i=1;i<=n;i++)cout<<f[i]<<' ';
// cout<<endl;
cout<<ans<<endl;
return 0;
}
LCA
定义:最近公共祖先简称 LCA。两个节点的最近公共祖先,就是这两个点的公共祖先里面,离根最远的那个。
性质:
-
前序遍历中,\(\text{LCA}(S)\) 出现在所有 \(S\) 中元素之前,后序遍历中 \(\text{LCA}(S)\) 则出现在所有 \(S\) 中元素之后。
-
两点集并的最近公共祖先为两点集分别的最近公共祖先的最近公共祖先,即 \(\text{LCA}(A\cup B)=\text{LCA}(\text{LCA}(A), \text{LCA}(B))\)。
-
两点的最近公共祖先必定处在树上两点间的最短路上。
-
\(d(u,v)=h(u)+h(v)-2h(\text{LCA}(u,v))\),其中 d 是树上两点间的距离,h 代表某点到树根的距离。
倍增算法
预处理出每个节点的第 \(2^i\) 的祖先节点,节约跳转次数。在查询两点的 LCA 时,先计算出两点深度差,将更深的节点跳转到与另一点相同深度,然后两点在第 \(2^i\) 的祖先节点不相同时共同向上跳转。最后 \(fa_{u,0}\) 即为最后答案。
Code.
#include<bits/stdc++.h>
#define endl "\n"
#define pb push_back
#define mkp make_pair
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
//value
const int inf=2147483647;
const int mod=1e9+7;
vector<int>g[500005];
int dfn[500005],fa[500005][25];
//function
void dfs(int x,int fat){
dfn[x]=dfn[fat]+1;
fa[x][0]=fat;
for(auto i:g[x]){
if(i==fat)continue;
dfs(i,x);
}
}
int lca(int x,int y){
if(dfn[x]>dfn[y])swap(x,y);
int tmp=dfn[y]-dfn[x];
for(int i=23;i>=0;i--){
if(dfn[fa[y][i]]>=dfn[x])y=fa[y][i];
}
if(x==y)return x;
for(int i=23;i>=0;i--){
if(fa[y][i]==fa[x][i])continue;
y=fa[y][i];
x=fa[x][i];
}
return fa[x][0];
}
void solve(){
return;
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
int n,m,s;
cin>>n>>m>>s;
for(int i=1;i<n;i++){
int u,v;
cin>>u>>v;
g[u].pb(v);
g[v].pb(u);
}
dfs(s,0);
for(int i=1;i<=23;i++){
for(int j=1;j<=n;j++){
fa[j][i]=fa[fa[j][i-1]][i-1];
}
}
for(int i=1;i<=m;i++){
int u,v;
cin>>u>>v;
cout<<lca(u,v)<<endl;
}
return 0;
}
预处理复杂度为 \(O(n \log n)\),单次查询为 \(O(\log n)\),优点在于方便好写。
欧拉序求 LCA
欧拉序是一个 dfs 与其回溯的序列具体如下:
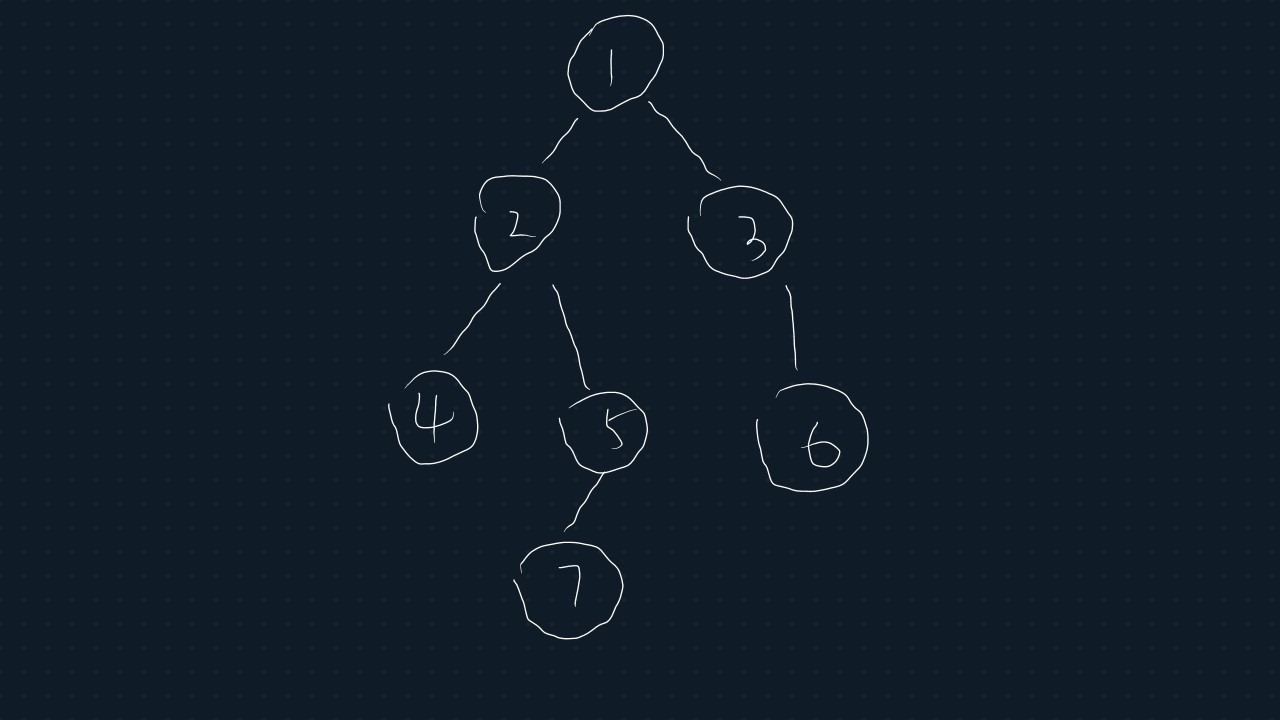
图中这颗树的欧拉序为\(1→2→4→2→5→7→5→2→1→3→6→3→1\)。
欧拉序求 LCA 只需要在欧拉序上将两点在欧拉序上的最早出现位置标出,找出两位置间深度最小的点即为两点的 LCA。在这一过程中,每个点在欧拉序中最早出现位置可以 \(O(n)\) 预处理,找深度最小可以用 ST 表 \(O(n \log n)\) 预处理 \(O(1)\) 查找。
Code.
#include<bits/stdc++.h>
#define endl "\n"
#define pb push_back
#define mkp make_pair
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
//value
const int inf=2147483647;
const int mod=1e9+7;
vector<int>g[500005];
int dep[500005],d[5000005],fir[500005],tx;
int st[5000005][25],lg[5000005];
//d为欧拉序,tx为长度,fir为点在欧拉序中初次出现位置
//st中存区间内深度最小的点
//function
void dfs(int x,int fa){
d[++tx]=x;
fir[x]=tx;
dep[x]=dep[fa]+1;
for(auto i:g[x]){
if(i==fa)continue;
dfs(i,x);
d[++tx]=x;
}
}
int lca(int x,int y){
if(fir[x]>fir[y])swap(x,y);
y=fir[y];
x=fir[x];
int l=lg[y-x+1];
int tmp1=st[x][l],tmp2=st[y-(1<<l)+1][l];
if(dep[tmp1]<dep[tmp2])return tmp1;
else return tmp2;
}
void solve(){
return;
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
int n,m,s;
cin>>n>>m>>s;
for(int i=1;i<n;i++){
int u,v;
cin>>u>>v;
g[u].push_back(v);
g[v].push_back(u);
}
//跑欧拉序
dfs(s,0);
// for(int i=1;i<=tx;i++)cout<<d[i]<<' ';
// cout<<endl;
//建ST
for(int i=2;i<=tx+2;i++)lg[i]=lg[i>>1]+1;
for(int i=1;i<=tx;i++)st[i][0]=d[i];
for(int i=1;i<=23;i++){
for(int j=1;j+(1<<i)<=tx;j++){
int tmp1=st[j][i-1],tmp2=st[j+(1<<(i-1))][i-1];
if(dep[tmp1]<dep[tmp2])st[j][i]=tmp1;
else st[j][i]=tmp2;
}
}
//找答案
for(int i=1;i<=m;i++){
int u,v;
cin>>u>>v;
cout<<lca(u,v)<<endl;
}
return 0;
}
DFS 序求 LCA
一个非常牛的科技,但我还没学会,所以先引下链接
树上差分
例题:P3128 [USACO15DEC] Max Flow P
在这道题中用到的是点差分,可以将 \(u\) 到 \(v\) 这一路径拆成 \(u\) 到 \(lca (u,v)\) 与 \(lca (u,v)\) 到 \(v\) 两条路径,将两条路径分别进行差分,最后统计答案即可。在差分时需要注意不要让 \(lca (u,v)\) 重复当右端点,否则会导致该点没有增加。
Code.
#include<bits/stdc++.h>
#define endl "\n"
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
//value
const int N=5e5+5;
int dn,dfn[N],fa[N][25],lg[N],sum[N],ans;
vector<int>g[N];
//function
void dfs(int id,int ft){
dfn[id]=dfn[ft]+1;
fa[id][0]=ft;
for(auto v:g[id]){
if(v!=ft)dfs(v,id);
}
}
int lca(int u,int v){
if(dfn[u]<dfn[v])swap(u,v);
while(dfn[u]>dfn[v]) u=fa[u][lg[dfn[u]-dfn[v]]-1];
if(u==v)return u;
for(int i=20;i>=0;i--){
if(fa[u][i]!=fa[v][i]){
u=fa[u][i];
v=fa[v][i];
}
}
return fa[u][0];
}
void get(int id,int ft){
for(auto v:g[id]){
if(v!=ft){
get(v,id);
sum[id]+=sum[v];
}
}
ans=max(ans,sum[id]);
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int n,k;
cin>>n>>k;
for(int i=1;i<n;i++){
int u,v;
cin>>u>>v;
g[u].push_back(v);
g[v].push_back(u);
}
dfs(1,0);
for(int i=1;i<=n;i++)lg[i]=lg[i-1]+(1<<lg[i-1] == i);
for(int i=1;i<=20;i++){
for(int j=1;j<=n;j++){
fa[j][i]=fa[ fa[j][i-1] ][i-1];
}
}
for(int i=1;i<=k;i++){
int u,v;
cin>>u>>v;
int L=lca(u,v);
sum[u]++;
sum[v]++;
sum[L]--;
sum[fa[L][0]]--;
}
get(1,0);
cout<<ans<<endl;
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号