图论(4) 最小生成树
最小生成树
最小生成树的定义为:无向连通图中边权和最小的生成树。
Kruskal 算法
Kruskal 算法是一种常见并且好写的最小生成树算法,本质是贪心思想。做法为从小到大向树林中插边直到成为一棵树。
算法虽简单,但需要相应的数据结构来支持,即应优先学会前置知识。具体来说,维护一个森林,查询两个结点是否在同一棵树中,连接两棵树。抽象一点地说,维护一堆集合,查询两个元素是否属于同一集合,合并两个集合。
其中,查询两点是否连通和连接两点可以使用并查集维护。时间复杂度在于排序与并查集。
Code.
#include<bits/stdc++.h>
#define endl "\n"
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
//value
const int inf=2147483647;
const int mod=1e9+7;
struct edge{
int u,v,w;
}a[200005];
int fa[200005];
//function
bool cmp(edge a,edge b){
return a.w<b.w;
}
int find(int x){
if(x==fa[x])return x;
return fa[x]=find(fa[x]);
}
void solve(){
return;
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
int n,m;
cin>>n>>m;
for(int i=1;i<=m;i++)cin>>a[i].u>>a[i].v>>a[i].w;
sort(a+1,a+1+m,cmp);
for(int i=1;i<=n;i++)fa[i]=i;
int cnt=1,ans=0;
for(int i=1;i<=m;i++){
int u=a[i].u,v=a[i].v,w=a[i].w;
if(find(u)==find(v))continue;
fa[find(u)]=find(v);
cnt++;
ans+=w;
if(cnt==n)break;
}
if(cnt==n)cout<<ans<<endl;
else cout<<"orz"<<endl;
return 0;
}
Prim 算法
与着眼于边的 Kruskal 不同,Prim 算法是通过点来一点点构建生成树的,基本思路是,我们维护当前已经构建好的部分生成树,然后不断尝试加点进去。
设当前构建好的生成树集合是 \(S\),剩余点集是 \(T\),并对 \(T\) 中的点记录与 \(S\) 中的点直接连接的最短边。我们每次选择 \(T\) 中距离最短的点加入 \(S\),即选择了一条最短边然后用这个新加入点更新其他点对应的距离。不断重复直到 \(T\) 是空集。
简单理解就是每次选择两个点集之间最短的边加入。
需要注意的是,Prim 算法有堆优化版本,但时间复杂度为 \(O(m\log n)\),与 Kruskal 算法差别不大,故在这里不给出代码。堆优化思路与最短路中的 dijkstra 算法相似,将点与该点到已构成树的距离加入小根堆,如果该点在这轮判断中加入了最小生成树点集,则用该点更新到其他点的距离,被更新的点加入小根堆。重复上述操作知道生成树。
Code.
#include<bits/stdc++.h>
#define endl "\n"
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
//value
const int inf=1e9+5;
int edge[5005][5005];
int vis[5005],dis[5005];
//function
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++)edge[i][j]=inf;
}
for(int i=1;i<=m;i++){
int x,y,z;
cin>>x>>y>>z;
edge[x][y]=min(edge[x][y],z);
edge[y][x]=min(edge[y][x],z);
}
for(int i=1;i<=n;i++)dis[i]=inf;
int x=1,ans=0,cnt=1;
for(int i=1;i<n;i++){
vis[x]=1;
for(int j=1;j<=n;j++){
dis[j]=min(dis[j],edge[x][j]);
}
x=0;
for(int j=1;j<=n;j++){
if(!vis[j]){
if(!x || dis[j]<dis[x]){
if(dis[j]<inf)x=j;
}
}
}
ans+=dis[x];
if(x)cnt++;
}
if(cnt<n)cout<<"orz"<<endl;
else cout<<ans<<endl;
return 0;
}
Borůvka 算法
一个讨论度极小的算法,在边具有一些特殊性质的图(边权为相邻两点计算得出的完全图)中该算法要显著优于前两个算法,例如经典的cf888G,时间复杂度为 \(O(m \log n)\)
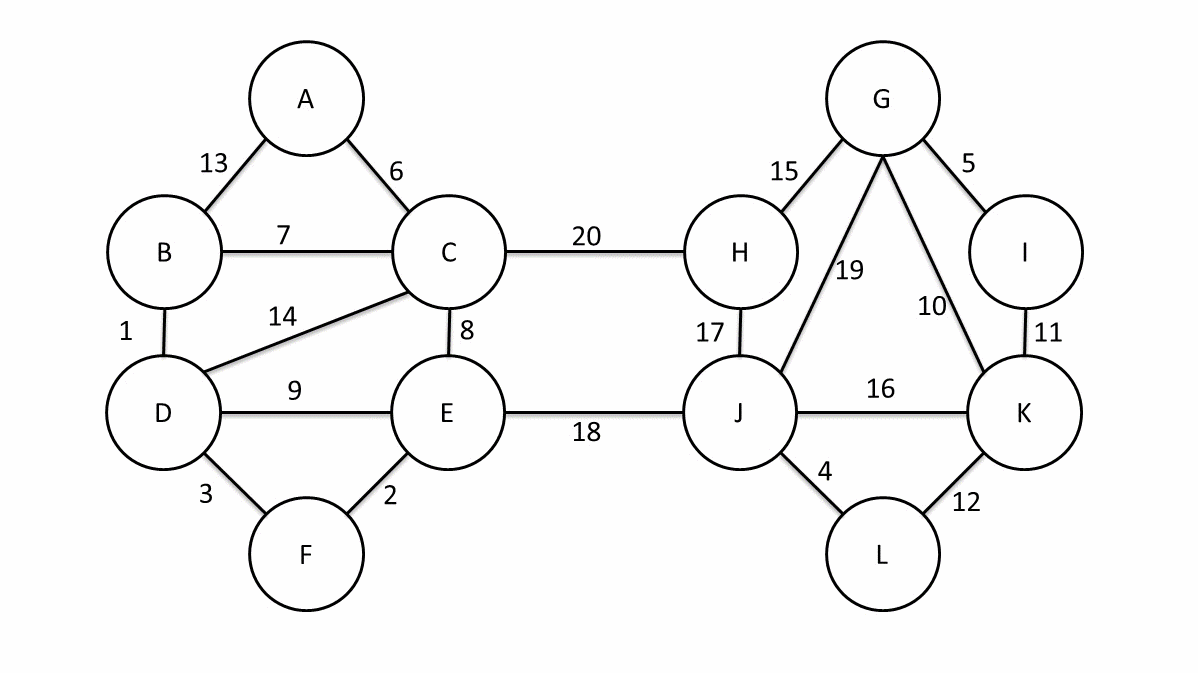
首先看下面这张图:
为了描述该算法,我们需要引入一些定义:
-
定义 \(E'\) 为我们当前找到的最小生成森林的边。在算法执行过程中,我们逐步向 \(E'\) 加边,定义连通块表示一个点集 \(V'\subseteq V\),且这个点集中的任意两个点 \(u\),\(v\) 在 \(E'\) 中的边构成的子图上是连通的(互相可达)。
-
定义一个连通块的 最小边 为它连向其它连通块的边中权值最小的那一条。
初始时,\(E'=\varnothing\),每个点各自是一个连通块:
-
计算每个点分别属于哪个连通块。将每个连通块都设为「没有最小边」。
-
遍历每条边 \((u, v)\),如果 \(u\) 和 \(v\) 不在同一个连通块,就用这条边的边权分别更新 \(u\) 和 \(v\) 所在连通块的最小边。
-
如果所有连通块都没有最小边,退出程序,此时的 \(E'\) 就是原图最小生成森林的边集。否则,将每个有最小边的连通块的最小边加入 \(E'\),返回第一步。
描述有点晦涩,可以结合代码和图理解。
Code.
#include<bits/stdc++.h>
#define endl "\n"
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
//value
const int inf=2147483647;
const int mod=1e9+7;
struct edge{
int u,v,w,id;
bool used;
//id 标记当前在哪个连通块
//used 标记该边使其在同一轮合并中不被重复使用
}a[200005];
int fa[200005],best[200005];
//best 中存的是该点所在的连通块每轮要拓展的边的id
//function
bool cmp(edge a,edge b){
return a.w<b.w;
}
int find(int x){
if(x==fa[x])return x;
return fa[x]=find(fa[x]);
}
void solve(){
return;
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
//1.输入+初始化
int n,m;
cin>>n>>m;
for(int i=1;i<=m;i++){
cin>>a[i].u>>a[i].v>>a[i].w;
a[i].used=false;
}
for(int i=1;i<=n;i++)fa[i]=i;
int ans=0,tot=1;
while(1){
bool flag=false;
//flag 避免该图不连通的情况
//这意味着该算法可以处理最小生成森林
for(int i=1;i<=n;i++)best[i]=0;
//2.查找每个连通块向外拓展最小边
for(int i=1;i<=m;i++){
//从边入手进行更新
int tmp1=find(a[i].u),tmp2=find(a[i].v);
if(tmp1==tmp2 || a[i].used)continue;
//如果该边对应连通块未找到向外连边或该边更优
if(a[i].w<a[best[tmp1]].w || best[tmp1]==0)best[tmp1]=i;
if(a[i].w<a[best[tmp2]].w || best[tmp2]==0)best[tmp2]=i;
}
//3.将标记的边联通
for(int i=1;i<=n;i++){
if(find(i)!=i)continue;
//保证连通块间只更新一次
if(best[i]!=0 && a[best[i]].used==false){
a[best[i]].used=true;
ans+=a[best[i]].w;
tot++;
fa[find(a[best[i]].v)]=find(a[best[i]].u);
flag=true;
}
}
// for(int i=1;i<=n;i++)cout<<best[i]<<' ';
// cout<<endl;
if(!flag)break;
}
if(tot!=n)cout<<"orz"<<endl;
else cout<<ans<<endl;
// cout<<tot<<' '<<ans<<endl;
return 0;
}
衍生算法或概念
特别要说的是,由于在2025版noi竞赛大纲中删除了次小生成树,且该算法在算法竞赛中比较 useless,故在此不特别提及此算法(俗称:懒),有兴趣者可以自行翻阅 OI Wiki 上的次小生成树。
瓶颈生成树
通俗的讲,瓶颈生成树就是在无向图中最大边权最小的一棵生成树。
性质比较显然,即为最小生成树是瓶颈生成树的充分不必要条件。
用人话来证明这个性质:
-
(充分性证明)如果最小生成树里的最长边大于瓶颈生成树里的最长边,显然我们可以删掉这条边,并用瓶颈生成树里的边连接更优,故最小生成树一定是瓶颈生成树。
-
(不必要性证明)瓶颈生成树显然只规定了最长边最小,但如果一些最小生成树中的边换成了较长边且边权不大于最长边,则该生成树依然是瓶颈生成树但不再是最小生成树。故瓶颈生成树不一定是最小生成树。
最小瓶颈路
通俗的讲,最小瓶颈路就是图中两点之间最大边权最小的一条简单路径。
性质
-
每种最小生成树上两点之间的路径都为两点的最小瓶颈路。
-
再同一个图上可能有不同的最小瓶颈路
-
不是所有最小瓶颈路都存在一棵最小生成树满足其为树上两点的简单路径。
由于性质 2 的存在,我们通常很难明确一条最小瓶颈路,但我们可以求出最小瓶颈路上的最大边权。基本思路是在求出最小生成树后用类似 \(LCA\) 的思路维护从深节点到浅节点的简单路径上的最大边权。
理论应该写一下的,但是我懒,有空再写。
Code.
Kruskal 重构树
一个非常精妙的算法。
在跑 Kruskal 的过程中我们会从小到大加入若干条边。而这次我们在加边的时候不在只是对两点进行边的连接,而是将边点化,建一个有点权的父节点连接两个集合,该节点的点权为加入边的边权,两个集合的根节点分别为父节点的左右儿子。
这个样子我们事实上就获得了一个恰有 \(n\) 个叶子节点的二叉树,且非叶子节点必有两个儿子。
这棵重构树具有以下性质:
-
原图中两个点之间的所有简单路径上最大边权的最小值 = 最小生成树上两个点之间的简单路径上的最大值 = Kruskal 重构树上两点之间的 \(LCA\) 的权值。
-
与 \(x\) 的最小瓶颈路上的最大边权 \(\leq val\) 的所有点 \(y\) 均在 Kruskal 重构树上的某一棵子树内,且恰好为该子树的所有叶子节点。
-
在 Kruskal 重构树上找到 \(x\) 到根的路径上权值 \(\leq val\) 的最浅的节点。这就是所有上一性质中 \(y\) 所在的子树的根节点。
注意到如果利用 Kruskal 重构树来解决瓶颈问题是非常优雅的。
如果我们要求的是最小边权最大值,思路相同,但是该问题求解中的最小生成树部分应修改为最大生成树。
理论应该写一下的,但是我懒,有空再写。
Code.


 浙公网安备 33010602011771号
浙公网安备 33010602011771号