图论(3) 最短路
图论(3) 最短路
基本概念
我们有时会想知道在一张图中,从一点走到另一点最短需要多少距离。在这一问题中,“一点”为起点,“另一点”为终点,这一问题的答案称作最短路,这一类问题称作最短路问题。
在最短路问题中,我们会根据图和题目需要的不同而采用不同的算法:
-
根据图中边权的不同,可分为正权最短路和负权最短路。
-
根据题目要求的不同,可分为单源最短路和多源最短路。
对于不同的题目,我们往往要使用不同的最短路算法,接下来会介绍三种覆盖了以上所有类型的最短路算法: \(Floyd\),\(dijkstra\) 和 \(Bellman–Ford\)。
Floyd 算法
\(Floyd\) 是一个用于解决多源最短路的算法,由于算法特点,此算法可以用于解决负权图上的最短路,但不能解决负环。其时空复杂度较高,但方便易写,常数小,是多源最短路的不二之选。时间复杂度是 \(O(n^3)\)。
思路
不断更新两点间的最短距离,更新方法是将两点间的路径分为起点到某点和某点到终点,并将两者边权和相加可得通过此点的两点间最短路答案。
代码实现简单:优先枚举断点(即上述思路的某点),然后枚举起点和终点,最后更新答案即可。
Code.
#include<bits/stdc++.h>
#define endl "\n"
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
//value
const int inf=2147483647;
const int mod=1e9+7;
int g[105][105];
//function
void solve(){
return;
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++)g[i][j]=1e9+7;
g[i][i]=0;
}
for(int i=1;i<=m;i++){
int u,v,w;
cin>>u>>v>>w;
g[u][v]=min(g[u][v],w);
g[v][u]=min(g[v][u],w);
}
for(int k=1;k<=n;k++){
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
g[i][j]=min(g[i][j],g[i][k]+g[k][j]);
}
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++)cout<<g[i][j]<<' ';
cout<<endl;
}
return 0;
}
Dijkstra 算法
\(Dijkstra\) 是一个用于解决单源正权最短路的算法,时间复杂度较为优异。时间复杂度是\(O(m\log m)\)
思路
从起始点开始,采用贪心算法的策略,每次遍历到始点距离最近且未访问过的顶点的邻接节点,直到扩展到终点为止。
算法过程
-
初始化,并将初始点加入待更新序列。
-
取出当前距离起始点最近且未访问的节点。
-
松弛操作,更新周围节点并加入待更新序列。
Code.
#include<bits/stdc++.h>
#define endl "\n"
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
//value
const int MA=1e5+10;
const int inf=0x7fffffff;
struct edge{
int v,w;
bool operator < (const edge &x) const {
if(w==x.w)return v<x.v;
else return w>x.w;
// return w==x.w?v<x.v:w>x.w;
//三目真难用
}
};
int n,m,s;
vector<edge>a[MA];
int ans[MA];
priority_queue<edge> pq;
bool vis[MA];
//function
void dijkstra(){
//初始点答案为0
ans[s]=0;
pq.push({s,ans[s]});
//开始遍历
while(!pq.empty()){
int tmp=pq.top().v;
pq.pop();
//仅遍历一次
if(vis[tmp])continue;
vis[tmp]=true;
//松弛
for(auto [v,w]:a[tmp]){
//如果更优就更新
if(!vis[v]&&ans[v]>ans[tmp]+w){
ans[v]=ans[tmp]+w;
pq.push({v,ans[v]});
}
}
}
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
//输入
cin>>n>>m>>s;
for(int i=0;i<m;i++){
int u,v,w;
cin>>u>>v>>w;
a[u].push_back({v,w});
}
//初始化
for(int i=0;i<MA;i++){
ans[i]=inf;
vis[i]=false;
}
dijkstra();
//输出
for(int i=1;i<=n;i++){
cout<<ans[i]<<' ';
}
return 0;
}
Bellman–Ford 算法
\(Bellman-Ford\) 算法是一个解决单源最短路问题的算法,可用于解决负权图上的最短路,也可判负环,时间复杂度劣于 \(Dijkstra\)。时间复杂度为 \(O(nm)\),由于时间复杂度太劣极易被卡。
思路
不断的用边更新到点的距离,由于每轮后到各点的最短路的个数加一,所以更新只会存在 \(n-1\) 轮。
算法过程
-
初始化
-
进行n轮松弛,判断第n轮是否进行了松弛操作
-
判环输出
Code.
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=2e5+9;
const ll inf=2147483647;
struct Edge{
ll v,w;
//v入点,w边权
};
vector<Edge>g[N];
ll d[N];
void solve(){
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int n,m,s;
cin>>n>>m>>s;
for(int i=1;i<=m;++i){
ll u,v,w;
cin>>u>>v>>w;
g[u].push_back({v,w});
}
//1.初始化
for(int i=1;i<=n;++i)d[i]=inf;
d[s]=0;
//2.进行n轮松弛,判断第n轮是否进行了松弛操作
bool circle=false;
//circle判环
for(int i=1;i<=n;i++){
circle=false;
//3.进行一轮松弛
for(int x=1;x<=n;x++){
for(Edge tmp:g[x]){
int y=tmp.v,w=tmp.w;
if(d[x]+w<d[y]){
d[y]=d[x]+w;
circle=true;
}
}
}
}
//理论而言我们只需要最后以此的circle
if(circle)cout<<2147483647<<'\n';
else{
for(int i=1;i<=n;i++)cout<<d[i]<<' ';
}
return 0;
}
SPFA 算法
此算法为 \(Bellman-Ford\) 算法的队列优化,时间复杂度优于 \(Bellman-Ford\) 算法,但仍易被卡到 \(O(nm)\)。
思路
对比 \(Bellman-Ford\) 算法,每轮更新只需要更新出点已经是最短路的边,但当一个点被更新次数超过 \(n-1\) 时即可判断存在负环。
Code.
#include<bits/stdc++.h>
#define endl "\n"
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
//value
const int inf=2147483647;
const int mod=1e9+7;
struct edge{
ll v,w;
};
vector<edge>g[10005];
ll cnt[10005],dis[10005],vis[10005];
queue<ll>q;
//function
void solve(){
return;
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
ll n,m,s;
cin>>n>>m>>s;
for(int i=1;i<=m;i++){
ll u,v,w;
cin>>u>>v>>w;
g[u].push_back({v,w});
}
for(int i=1;i<=n;i++)dis[i]=inf;
dis[s]=0;
q.push(s);
while(!q.empty()){
ll t=q.front();
q.pop();
for(int i=0;i<g[t].size();i++){
edge j=g[t][i];
if(dis[j.v]>dis[t]+j.w){
dis[j.v]=dis[t]+j.w;
q.push(j.v);
cnt[j.v]++;
}
if(cnt[j.v]>=n){
cout<<2147483647<<endl;
return 0;
}
}
}
for(int i=1;i<=n;i++)cout<<dis[i]<<' ';
return 0;
}
相关应用
最短路作为图论中较为基本的算法,应用非常广泛且拓展方法很多,下面将会介绍几种以最短路为解决问题的方法和技巧。
差分约束
定义
在 \(OIwiki\) 上,差分约束是这么定义的(事实上是我懒):
差分约束系统是一种特殊的 \(n\) 元一次不等式组,它包含 \(n\) 个变量 \(x_1, x_2, \ldots, x_n\) 以及 $m $ 个约束条件。每个约束条件是由两个其中的变量做差构成的,形如 \(x_i - x_j \leq c_k\)其中 \(1 \leq i, j \leq n, \quad i \neq j, \quad 1 \leq k \leq m\) 且 \(c_k\) 是常数(可以是非负数,也可以是负数)。需要解决的问题是:求一组解 \(x_1 = a_1, \quad x_2 = a_2, \quad \ldots, \quad x_n = a_n\) 使得所有的约束条件得到满足,否则判断出无解。
思路
我们将每个约束条件进行一项后可以发现,这个式子惊人的和最短路每次用边更新的条件相似。故我们尝试建图,并把每个 \(x_i\) 作为图中的一个点,对于每个类似 \(x_i - x_j \leq c_k\) 的约束进行 \(j\) 到 \(i\) 的连边,边权为 \(c_k\)。
在建好的图上跑一遍 \(Bellman-Ford\) 或 \(SPFA\),若存在负环,则无解,若不存在负环,则必然有 \(x_i = dist_i\) 的解。
对上述解法有如下的正确性证明:
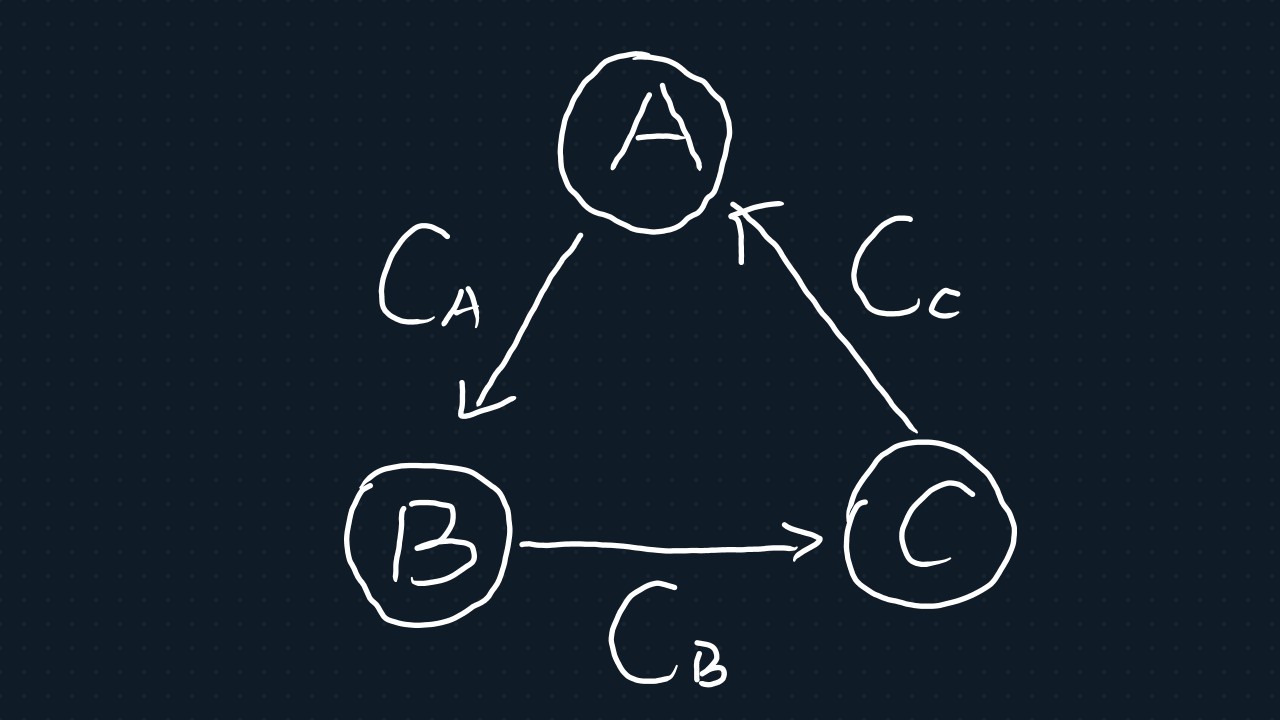
若存在负环,则有 \(c_A + c_B + c_C < 0\),且同时存在\(A - B \leq c_A\),\(B - C \leq c_B\),\(C - A \leq c_C\)。由 \(2\) 式 \(3\) 式相加后联立 \(1\) 式可得 \(-c_A - c_B \leq C-A \leq c_C\),化简后与\(c_A + c_B + c_C < 0\) 相斥,故存在负环时对于此差分约束无解。
特别的,有些时候负环与起点可能不在同一连通块,需建立一个超级原点与每个点有一条边权为 \(0\) 的边。
Code.
#include<bits/stdc++.h>
#define endl "\n"
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
//value
const int inf=2147483647;
const int mod=1e9+7;
int dis[200005],cnt[200005];
struct edge{
int v,w;
};
vector<edge>g[200005];
queue<int>q;
//function
void solve(){
return;
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
int n,m;
cin>>n>>m;
for(int i=1;i<=m;i++){
int cmp;
cin>>cmp;
if(cmp==1){
int a,b,c;
cin>>a>>b>>c;
g[a].push_back({b,-c});
}
else if(cmp==2){
int a,b,c;
cin>>a>>b>>c;
g[b].push_back({a,c});
}
else {
int a,b;
cin>>a>>b;
g[a].push_back({b,0});
g[b].push_back({a,0});
}
}
for(int i=1;i<=n;i++)dis[i]=inf;
for(int i=1;i<=n;i++)g[0].push_back({i,0});
q.push(0);
while(!q.empty()){
int tmp=q.front();
q.pop();
for(auto i:g[tmp]){
int v=i.v,w=i.w;
if(dis[v]>dis[tmp]+w){
dis[v]=dis[tmp]+w;
q.push(v);
cnt[v]++;
}
if(cnt[v]>=n){
cout<<"No"<<endl;
return 0;
}
}
}
cout<<"Yes"<<endl;
return 0;
}
分层图最短路
Alice 和 Bob 现在要乘飞机旅行,他们选择了一家相对便宜的航空公司。该航空公司一共在 \(n\) 个城市设有业务,设这些城市分别标记为 \(0\) 到 \(n-1\),一共有 \(m\) 种航线,每种航线连接两个城市,并且航线有一定的价格。
Alice 和 Bob 现在要从一个城市沿着航线到达另一个城市,途中可以进行转机。航空公司对他们这次旅行也推出优惠,他们可以免费在最多 \(k\) 种航线上搭乘飞机。那么 Alice 和 Bob 这次出行最少花费多少?
分层图最短路便是类似与以上题目(洛谷 \(P4568\) )的一种题目类型。
思路
运用拆点的思想,将原图拆成相同的 \(k\) 层图,不同层之间的连边为边权为 \(0\) 同层中连边。在这一分层图中跑最短路即可。
特别的,如果层数多于最短路所走的边数,答案为 \(0\)。
在个别题目中,我们还会用到建虚点的思想,其本质为建立一个不存在的点使复杂图简化或达到某些不好在原图上直接应用的性质,这一思路在网络流算法中亦有体现。
Code.
#include<bits/stdc++.h>
#define endl "\n"
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
//value
const ll MA=2e6+10;
const ll inf=0x7fffffff;
struct edge{
ll v,w;
bool operator < (const edge &x) const {
return w==x.w?v<x.v:w>x.w;
}
};
ll n,m,k,s,t;
vector<edge>a[MA];
ll ans[MA];
priority_queue<edge> pq;
bool vis[MA];
//function
void dijkstra(){
ans[s]=0;
pq.push({s,ans[s]});
while(!pq.empty()){
ll tmp=pq.top().v;
pq.pop();
if(vis[tmp])continue;
vis[tmp]=true;
for(edge i:a[tmp]){
ll v=i.v;
ll w=i.w;
if(!vis[v]&&ans[v]>ans[tmp]+w){
ans[v]=ans[tmp]+w;
pq.push({v,ans[v]});
}
}
}
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>n>>m>>k;
cin>>s>>t;
for(int i=0;i<m;i++){
ll u,v,w;
cin>>u>>v>>w;
a[u].push_back({v,w});
a[v].push_back({u,w});
for(int j=1;j<=k;j++){
a[u+(j-1)*n].push_back({v+j*n,0});
a[v+(j-1)*n].push_back({u+j*n,0});
a[u+j*n].push_back({v+j*n,w});
a[v+j*n].push_back({u+j*n,w});
}
}
/*
for(int i=1;i<=k;++i)
{
add_edge(t+(i-1)*n,t+i*n);
}
*/
for(int i=1;i<=k;i++){
a[t+(i-1)*n].push_back({t+i*n,0});
}
for(int i=0;i<MA;i++){
ans[i]=inf;
vis[i]=false;
}
dijkstra();
if(s!=t)cout<<ans[(k)*n+t]<<endl;
else cout<<0<<endl;
return 0;
}
同余最短路
当出现形如「给定 \(n\) 个整数,求这 \(n\) 个整数能拼凑出多少的其他整数(\(n\) 个整数可以重复取)」,以及「给定 \(n\) 个整数,求这 \(n\) 个整数不能拼凑出的最小(最大)的整数」,或者「至少要拼几次才能拼出模 \(K\) 余 \(p\) 的数」的问题时可以使用同余最短路的方法。
同余最短路利用同余来构造一些状态,可以达到优化空间复杂度的目的。
类比 差分约束 方法,利用同余构造的这些状态可以看作单源最短路中的点。同余最短路的状态转移通常是这样的 \(f(i+y) = f(i) + y\),类似单源最短路中 \(f(v) = f(u) +edge(u,v)\)。
思路
例题:P3403 跳楼机
首先有一个显然的性质:若 \(d\) 层可以只用方法 \(2\) 和 \(3\) 爬上,则显然 \(d + x\),\(d + 2x\)...都可以爬上。
令 \(d_i\) 表示只通过方法 \(2\) 和 \(3\) 可以爬上第 \(p\) 层且满足 \(p \mod x = i\) 的最小值 \(p\),则显然有 \(d_i + y \geq d_{((i + y)\mod x)}\),\(d_i + z \geq d_{((i + z)\mod x)}\),可以发现这个东西可以建图后用最短路解决。求出 \(d_i\) 后利用性质统计答案即可。
Code.
#include<bits/stdc++.h>
#define endl "\n"
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
//value
const ll MA=2e5+10;
const ll inf=2e18+9;
struct edge{
ll v,w;
bool operator < (const edge &x) const {
if(w==x.w)return v<x.v;
else return w>x.w;
}
};
vector<edge>g[MA];
ll dis[MA];
priority_queue<edge> pq;
bool vis[MA];
//function
void dijkstra(){
for(int i=0;i<MA;i++)dis[i]=inf;
dis[0]=0;
pq.push({0,dis[0]});
while(!pq.empty()){
ll tmp=pq.top().v;
pq.pop();
if(vis[tmp])continue;
vis[tmp]=true;
for(auto [v,w]:g[tmp]){
if(!vis[v] && dis[v]>dis[tmp]+w){
dis[v]=dis[tmp]+w;
pq.push({v,dis[v]});
}
}
}
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
ll h,x,y,z;
cin>>h;
cin>>x>>y>>z;
if(x==1 || y==1 || z==1){
cout<<h<<endl;
return 0;
}
h--;
for(int i=0;i<x;i++){
//显然只需求出小于x的d_i即可
g[i].push_back({(i+y)%x,y});
g[i].push_back({(i+z)%x,z});
}
dijkstra();
ll ans=0;
for(int i=0;i<x;i++){
if(dis[i]<=h)ans+=(h-dis[i])/x+1;
}
cout<<ans<<endl;
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号