迪杰斯特拉算法（步步贪心）

迪杰斯特拉算法

1.迪杰斯特拉算法是求原点到各个点的最短距离，用的是步步贪心的方法所以不能解决带负权图，这个到后边说

2.迪杰斯特拉算法的实现

要用到的数组  ：
（1）graph[ ] [ ]用来存图

（2）flag[ ]用来记录此点是否已经被加入

（3）path[ i ]用来表示从原点到达 i 节点的前驱，输出时直到找到前驱为原点即可，用来存路径。具体参见弗洛伊德算法中的路径

（4）dist[ ]记录原点到各个点的即时最短路径 

3.代码的实现

（1）初始化各个数组

graph[][] //输入自行建图
flag[] = 0//开始时全部的点都没用到
path[ ] = sor  //开始时前一个点是原点

for()
dist[i] = graph[sor][i]//初始化dist[ ] 

flag[sor] = true//原点不用往里加
dist[sor] = 0//到自己不用算

（2）依次贪心加入点并做标记，直到全部加入

for(int i = 1; i < v; i++)
     {
         int minx = 9999999;//设置一个无限大的量相对于graph
            int k = 0;//记录要加入的点
         for(int j = 0; j < v; j++)
         {
             if(dist[j] < minx&&!flag[j])
             {
                 k = j;
                 minx = dist[j];
             }
        }
        flag[k] = true;//使用过的点做标记
        for(int j = 0; j < v; j++)
        {
            if(dist[j] > minx + graph[k][j])
            {
                 dist[j] = minx + graph[k][j];
                                path[ j ] = k;
            }
        }
     }

(3)

输出dist 和 path即可

 4.不能算负权图的解释

如图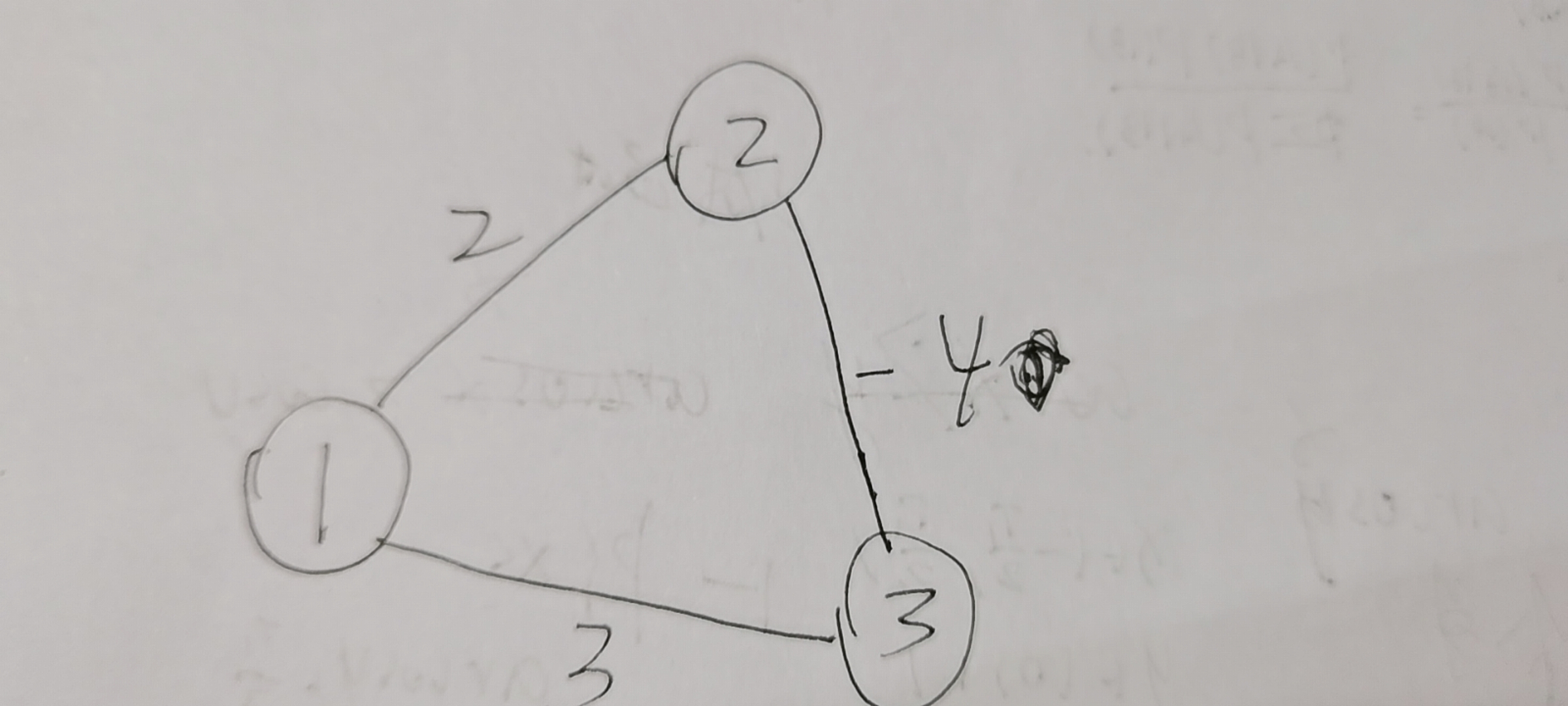

原点为1 由于步步贪心，我们开始时加入的是2 点然后我们更新到三的距离为  -2 ，然后我们在加入 3，更新 2 显然结果不对