最短路

1.问题

　从一个起点到达一个终点所需要经过的最短的路径。

2.解析

这里先说两种算法：floyd、dijkstra。

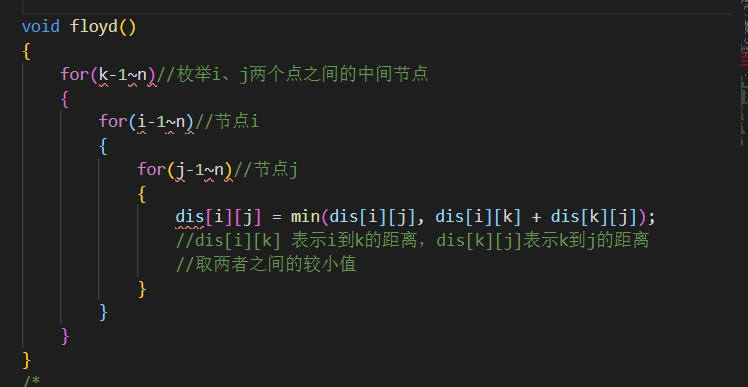
floyd是一种动态规划的算法。

从任意的i点到达任意j点的最短距离有两种情况：

1.直接从i到j

2.i经过若干个中间节点到达j

那么你就可以去暴力枚举中间节点，用动态规划的思想，去更新两点之间的距离，使得你得到的i到j的距离是最短的。

例子：

原始：

 

 

 

 

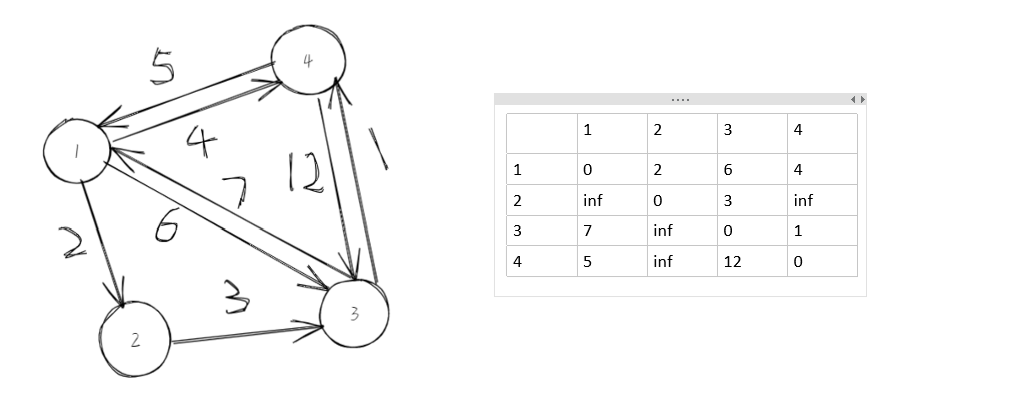
 第一步，选择中间节点为1,更新其节点：

 

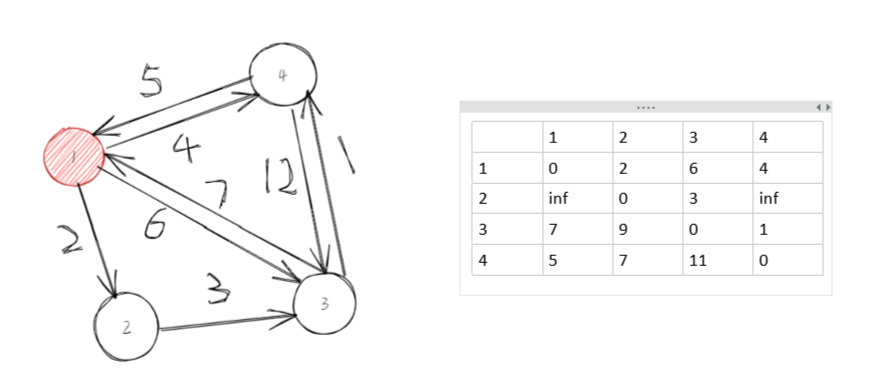
第二步，以2为中间节点去更新：

 

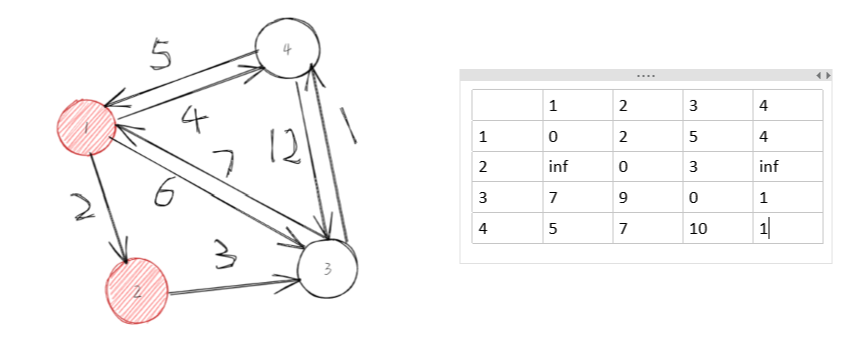
 第三步，选择3节点为中间节点去更新:

 

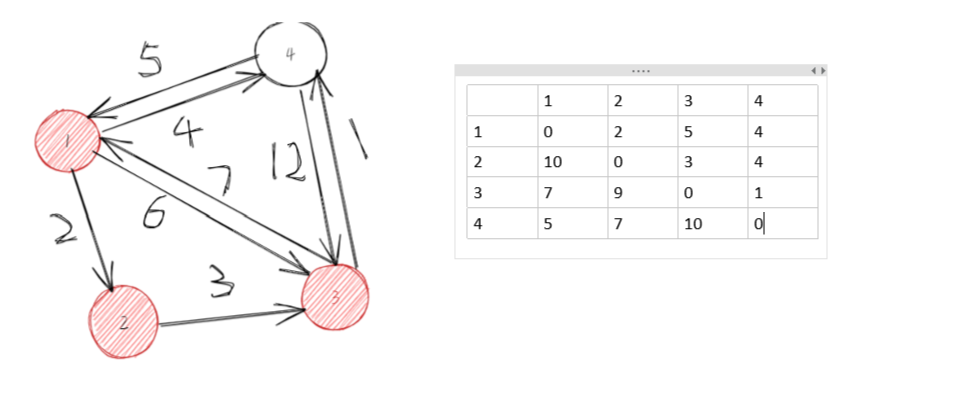
 第四步，选择4节点为中间节点取更新

 

 

 

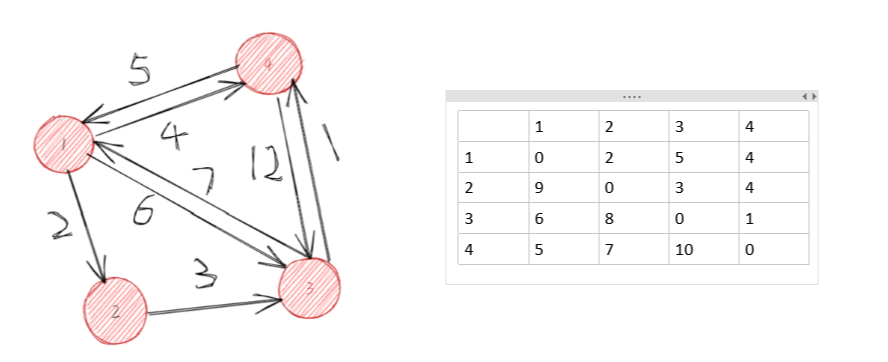
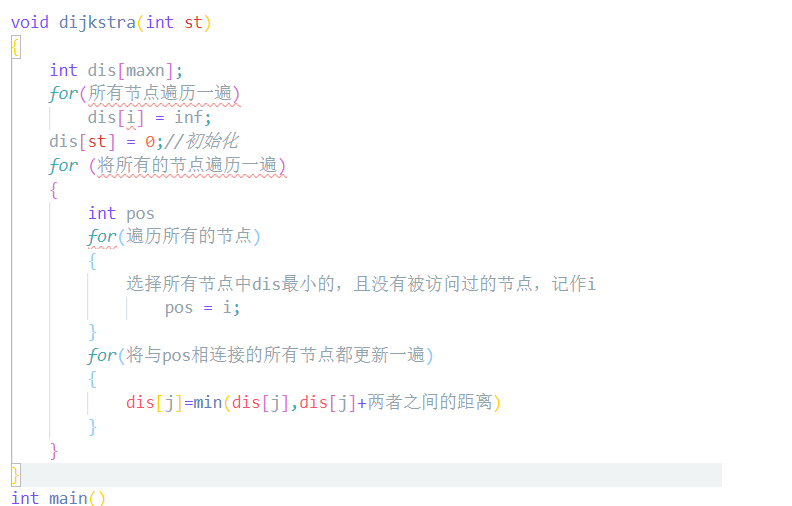
dijkstra:

dijkstra运用的是一种贪心的思维，用一个dis数组去来记录，其他所有点到起点之间的距离。

每次选择dis最小的节点，去更新与之相连接的节点，重复直到所有节点都被选择过。

例子：

以1为起点到达8

初始化：

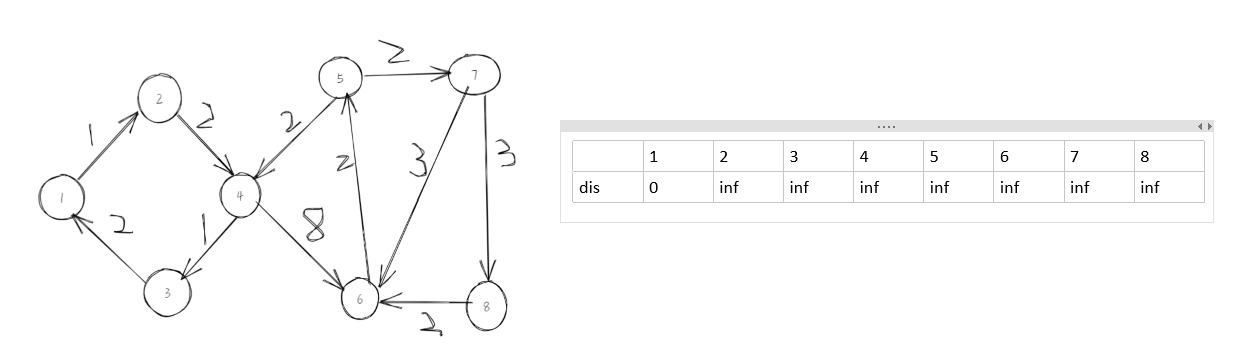
 第一步，选择dis最小的1，取更新与他右边相连接的点：

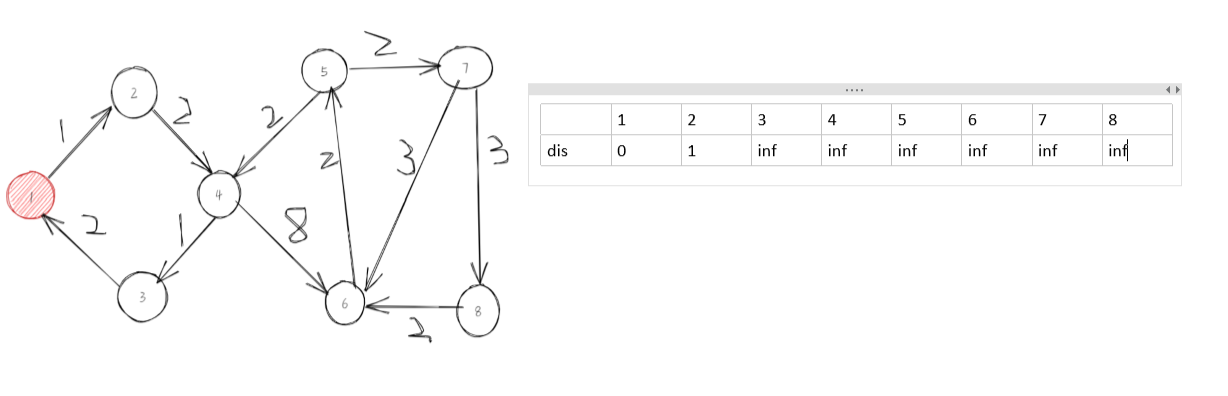
 第二步，选择没有被访问过，且dis最小的2，更新：

 

 

 

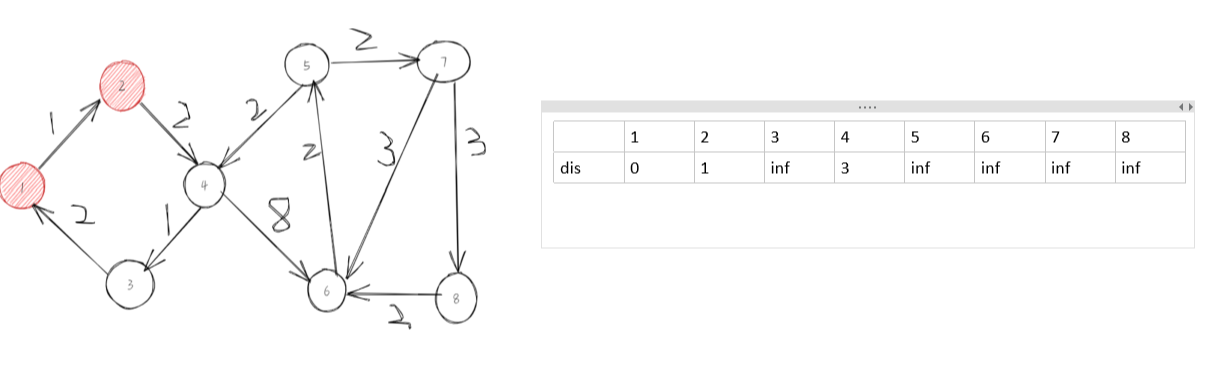
 第三步，选择4节点，更新与他相连接的节点。

 

 

 

 第四步，选择3节点，去更新答案，并不可以更新。

 

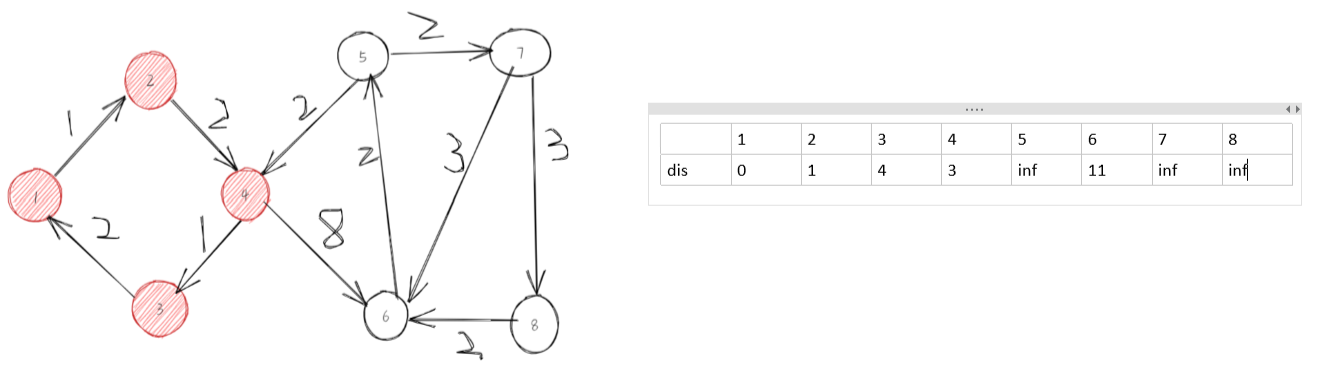
 第五步，选择6节点，去更新相应的节点。

 

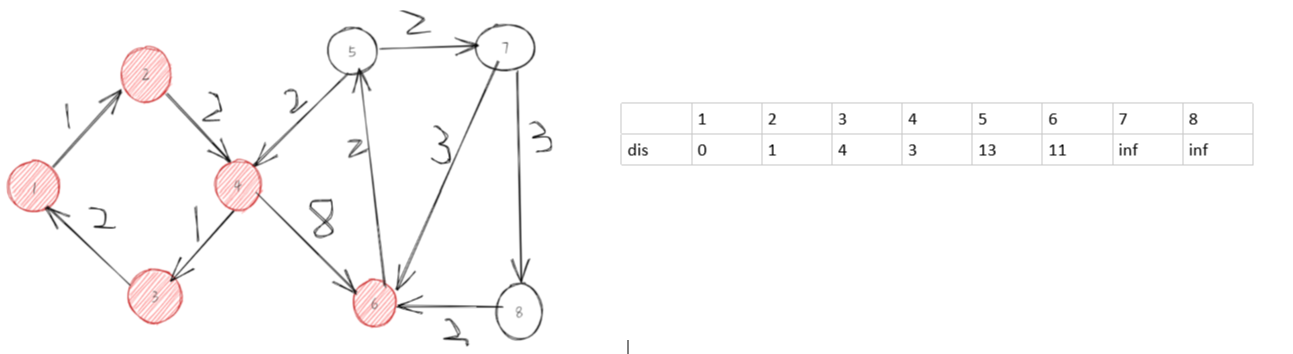
第六步，选择5节点，去更新与之相连接的节点。

 

 

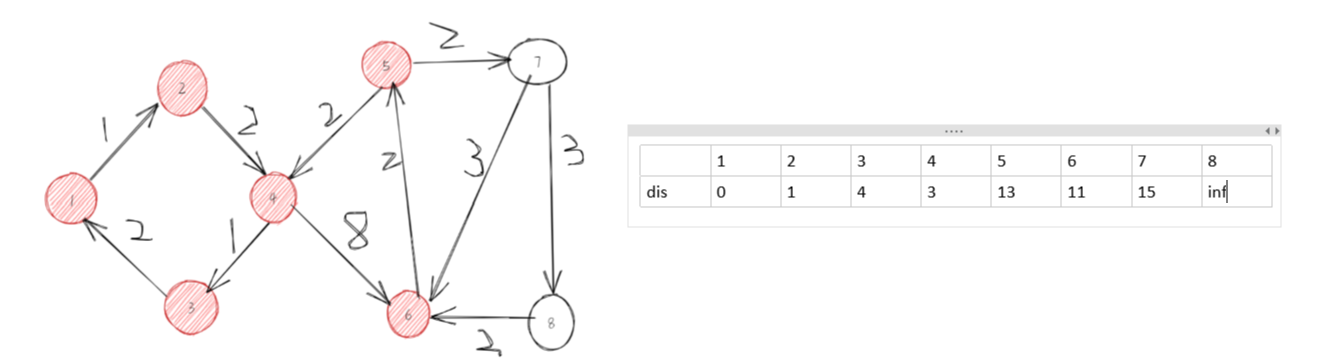
 第七步，选择7，去更新与之相连接的节点。

 

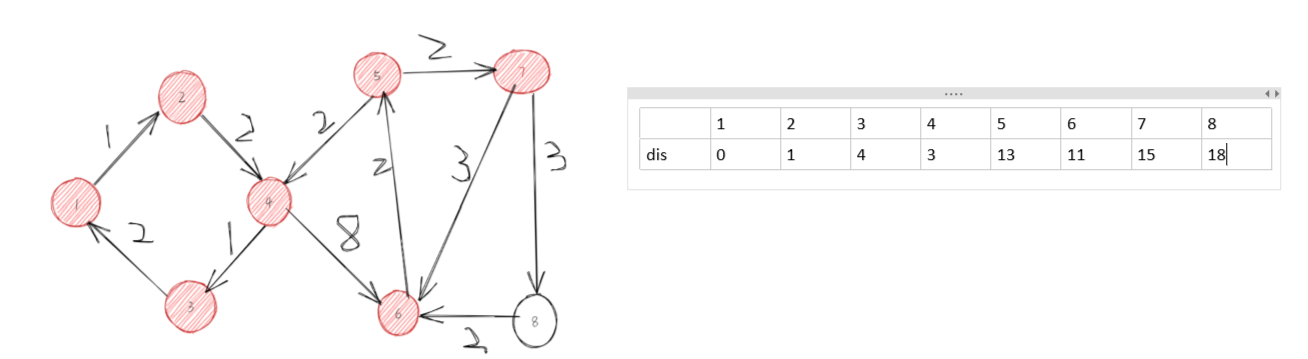
第八步，选择8，去更新。

 

 

 

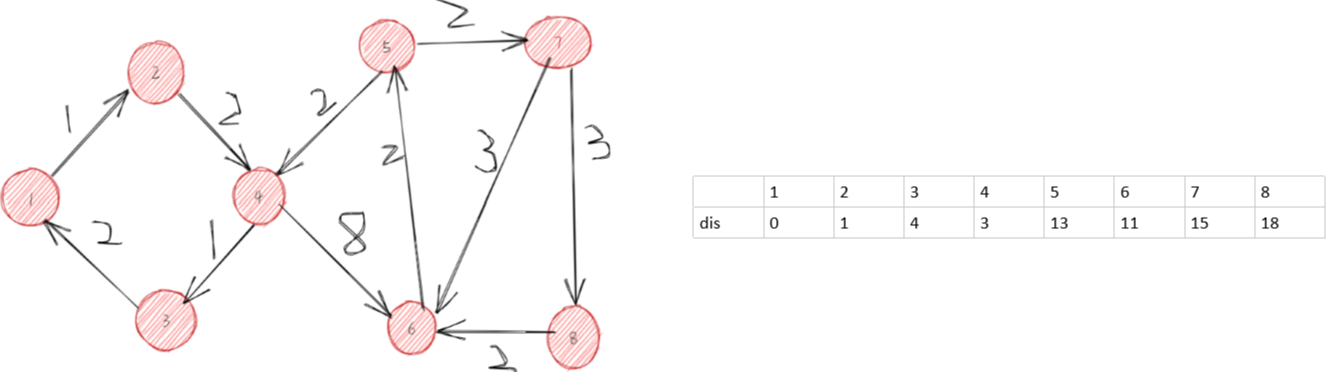
这样以此完整的dijkatra就更新完成了！！！

3,设计

 

 

4.分析

floyd:时间复杂度O(n^3) 空间复杂度O(n^2)  适合稠密图，无负环的图，能直接求出所有点之间的最短路。

dijkstra:时间复杂度O(n^2)（可以用堆优化到O(n*log(n))） 用来求单源最短路，无负边的图。

5.源码

 Github