最小生成树

1.问题

w(t)=$$\sum_{(u,v)\in t}^n$W(u,v),在一给定的无向图G = (V, E) 中，(u, v) 代表连接顶点 u 与顶点 v 的边（即），而 w(u, v) 代表此边的权重，若存在 T 为 E 的子集（即）且为无循环图，使得

的 w(T) 最小，则此 T 为 G 的最小生成树。

2.解析

有两种算法：分别是kruskal和prim算法

 kruskal：

kruskal总时维护无向图的最小生成森林，最初森林由两条边构成，然后逐渐的去增加边。

1.从剩余的边中选择权值最小的边，判断两个节点是否在一棵树中

2.如果是在一棵树中那么就掠过这条边，重复步骤1

3.若这两个节点不是在一棵树中，把该条边加入生成森林当中。

例子: 

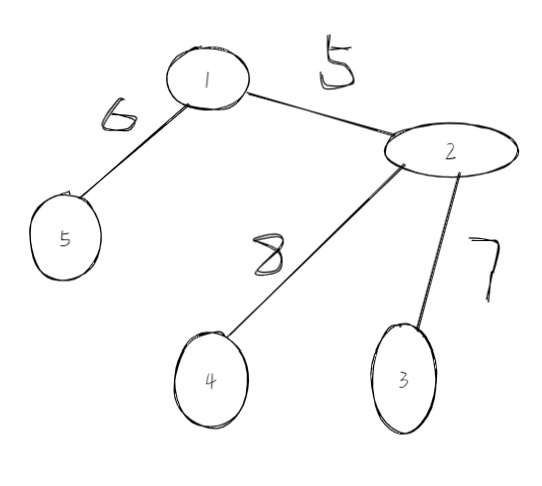
n=5,m=7

edge（分别表示两个节点和边值）:

1 2 5
2 3 7
2 4 8
4 5 11
3 5 7
1 5 6
4 2 12

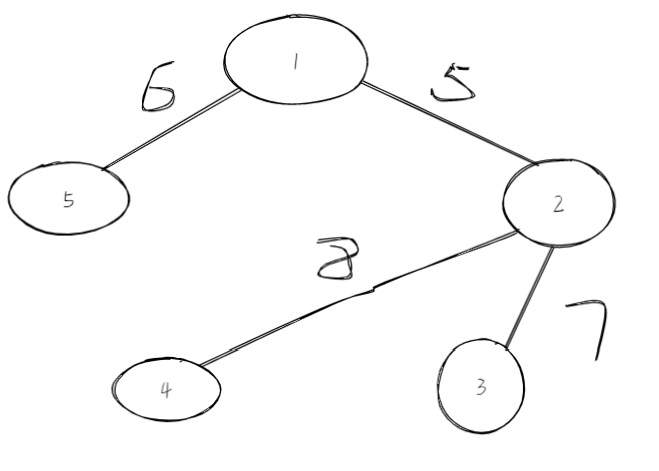
Step1：边长最小的5，两个不在一个树中，加入                    　　Step2：选择边长最小的6，两点也不在一棵树中，加入　　　　　　　　　　　　　　　　　　　　　　　　　　　

              

 

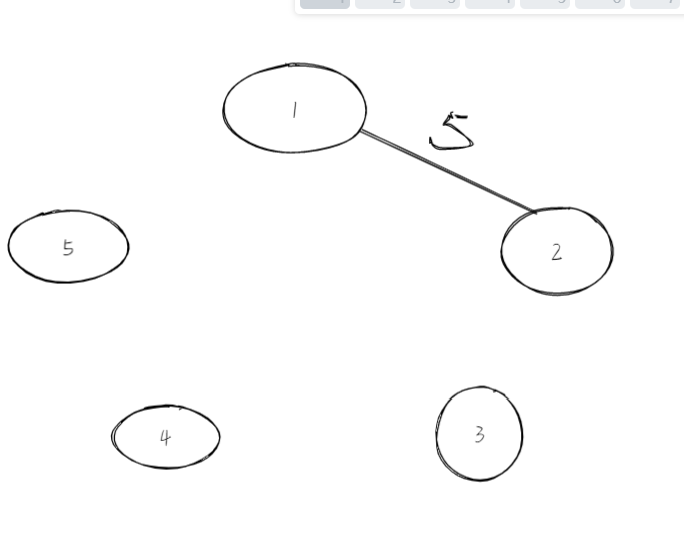
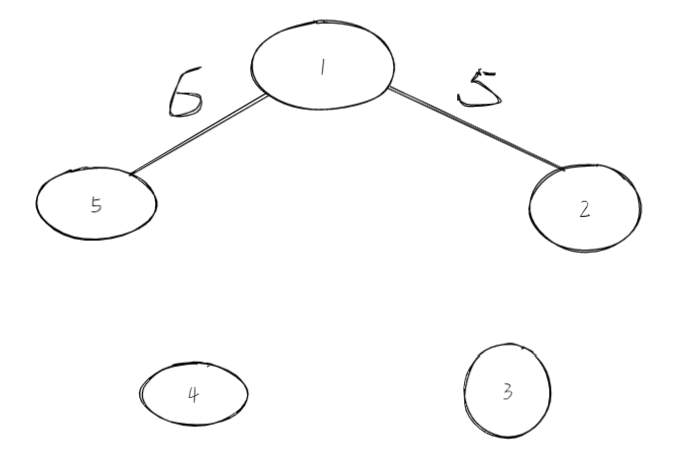
Step3:权值最小的7，选择2和3　　　　　　　　　　　　　　Step4：3和5在一个树中，所以不选  

          

 

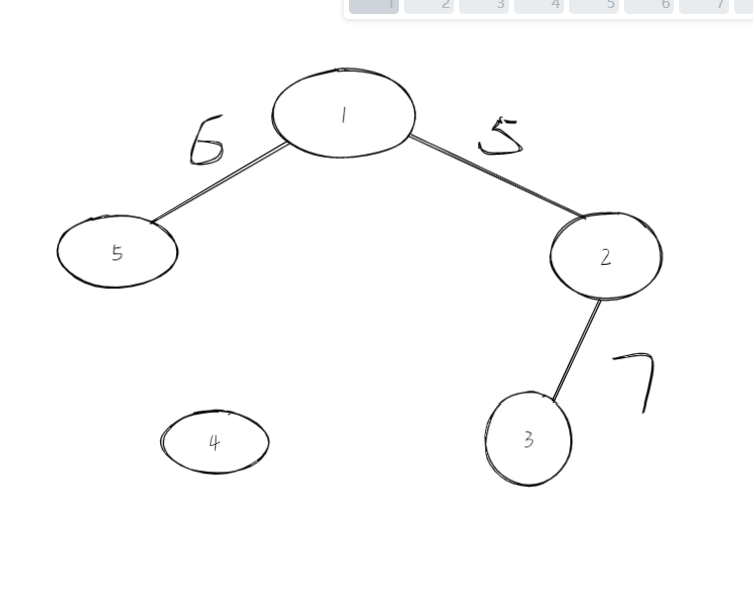
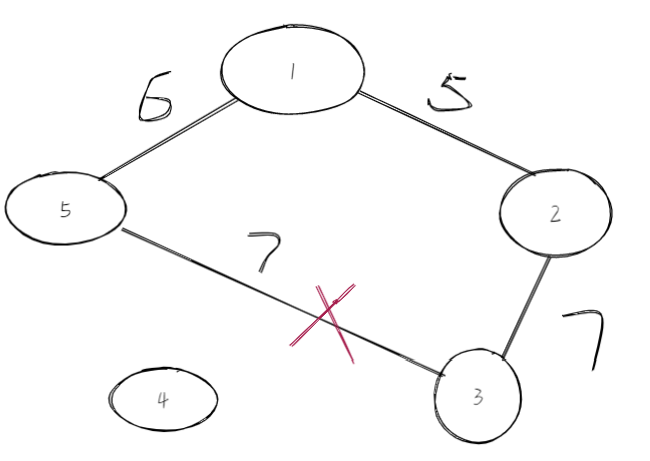
Step5:选择边权为8的边，加入，选购了n-1条边，所以结束。

prim：

prim算法总是维护最小生成树的一部分。

1.设已经确定属于最小生成树的节点集合为T（初始时候节点包含1），剩余边的集合为S。

2.找到一条边两个端点x,y分别在T和S中，且是权值最小的边，将y从S中去除，加入到T中，并加上权值。

3.重复2。

 例子：

n=5,m=7

edge（分别表示两个节点和边值）:

1 2 5
2 3 7
2 4 8
4 5 11
3 5 7
1 5 6
4 2 12

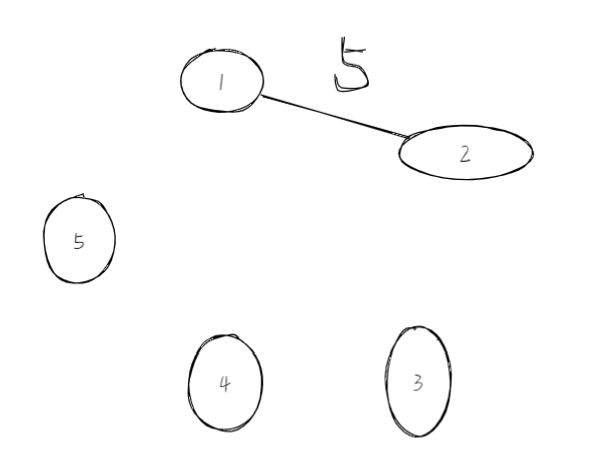
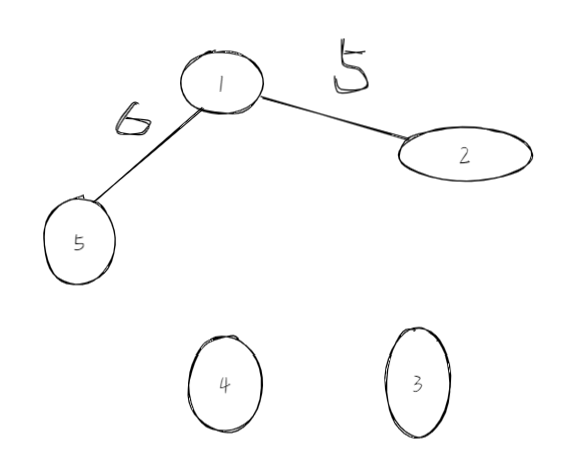
Step1:　　　　　　　　　　　　　　　　　　　　　　　　　 Step2:　　

      

 

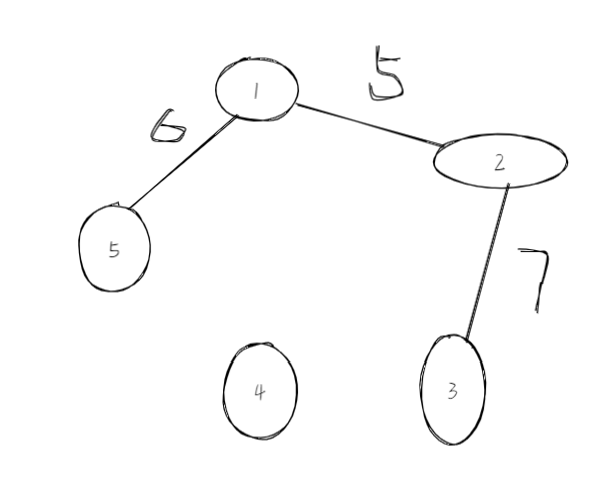
Step3:　　　　　　　　　　　　　　　　　　　　　　　　Step4:

        

3.设计

 

void kruskal()
{
    将所有的边按照从小到大的顺序排序一遍 
    int cnt=0;//用来存放有多少条边
    ans=0;//用来存放MST的值
    for(将所有的边遍历一遍)
    {
        判断两个节点是否在一棵树中
        if(在一棵树中) continue;
        更新ans和cnt，并且将这两个节点更新到一棵树中 
    } 
}

 

void prim()
{
    for(遍历所有点)
    {
        找出当前最小生成树节点集合中最小的边，同时这个边连接的另外一个点不在这个集合中
        去更新集合 
    }
}

 

4.分析

kruskal复杂度O(mlog m) (适合稀疏图)

prim复杂度O(n^2),堆优化能达到O(n^2) （适合稠密图）

5.源码

Github地址