万花尺——探究数学建模和信息化在处理生活问题中的应用

万花尺——探究数学建模和信息化在处理生活问题中的应用

作者：Pass1on_W

日期：2022年10月

一、简单介绍

我们可以使用万花尺玩具来绘制曲线。这种玩具由两个不同尺寸的齿轮构成。我们只需把小齿轮嵌入大齿轮中，之后把笔放入小齿轮的小孔中，用力使小齿轮发生旋转，这样我们就可以得到一个独特的螺线。这便是一个齿轮结构，齿轮与齿轮之间的啮合与旋转，形成了这极具美感的图形。接下来我将从数学建模的角度来探究这种图形的生成过程。

二、原理讲解

1.万花尺的基本原理

​ 玩过万花尺的人都清楚，使用万花尺的过程中我们需要不停地旋转小齿轮，而旋转的圈数到底是多少，这取决于两个齿轮的参数，而现在我们就要探究这个参数和所绘制出来的图案之间的关系。

2.参数方程与内旋轮线

​ 首先我们来考虑大圆的参数方程。显然的，大圆的参数方程满足 \(cos^2(\theta)+sin^2(\theta)=r^2\)

​ 之后我们来考虑螺线的参数方程。

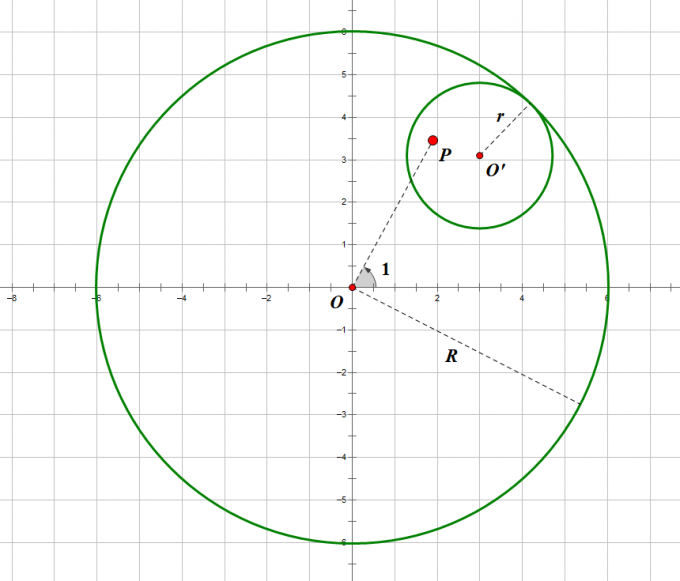
​ 如图所示

​ 我们定义：\(O\) 为大圆圆心，\(R\) 为大圆半径，\(O'\) 为小圆圆心，\(r\) 为小圆半径，点 \(P\) 为笔尖所在位置，\(l=\frac{PC}{r}\) 为线段 \(PO'\) 与小圆半径 \(r\) 之比

​ 稍作推导，不难得到内旋轮线的参数方程：

\[x=R((1-k)cos\theta+lkcos(\frac{1-k}{k}\theta)) \]

\[y=R((1-k)sin\theta+lksin(\frac{1-k}{k}\theta)) \]

3.万花尺的周期性

​ 当我们需要确定什么时候完成了这次的绘制（即新绘制的图像已经和原来所绘制的图像重合了），我们就需要利用万花尺的周期性，来研究大小圆的半径比的关系。

​ 我们不妨假设\(r=35，R=49\)

​ 首先需要处理\(k=\frac{r}{R}\)，即化简分数，这里我们需要用到最大公约数\(（GCD）\)的相关知识

​ 该分数化简完可以写成 \(\frac{5}{7}\)

​ 这告诉我们：\(5\) 圈之后，图像将开始重复，而这个过程中，小圆旋转了 \(7\) 周

​ 通过上面的内容，我们可以发现 \(k=\frac{r}{R}\) 决定了曲线的形状。

三、程序代码（只呈现关键代码）

class Spiro:

    def __init__(self, xc, yc, col, R, r, l):
        # 创造一个turtle对象
        self.t = turtle.Turtle()
        # 设置光标形状
        self.t.shape('turtle')

        # 将参数绘图角度的增量设置为5度
        self.step = 5
        # 设置绘制完成标志
        self.drawingComplete = False

        # 设置参数
        self.set_params(xc, yc, col, R, r, l)

        # 初始化绘制
        self.restart()

    def set_params(self, xc, yc, col, R, r, l):
        """初始化Spiro对象"""
        # Spiro的参数
        # 保存曲线中心的坐标
        self.xc = xc
        self.yc = yc
        # 将圆的半径转化为整数并存储
        self.R = int(R)
        self.r = int(r)
        self.l = l
        self.col = col

        # 用GCD除法将 r/R 化简到最简形式
        # 利用这些信息确定曲线的周期性
        gcd_value = math.gcd(self.r, self.R)
        self.nRot = self.r // gcd_value

        # 得到半径的比值
        self.k = r / float(R)

        # 设置颜色
        self.t.color(*col)

        # 存储当前角度
        self.a = 0

    def restart(self):
        """重置Spiro对象的绘制参数"""
        # 初始化绘制完成标志
        self.drawingComplete = False
        # 显示turtle光标
        self.t.showturtle()
        # 前往第一个落笔点
        self.t.up()
        R, k, l = self.R, self.k, self.l
        a = 0.0
        x = R * ((1 - k) * math.cos(a) + l * k * math.cos((1 - k) * a / k))
        y = R * ((1 - k) * math.sin(a) - l * k * math.sin((1 - k) * a / k))
        self.t.setpos(self.xc + x, self.yc + y)
        self.t.down()

    def draw(self):
        """用连续的线段绘制曲线"""
        # 画出剩下的点
        R, k, l = self.R, self.k, self.l
        for i in range(0, 360 * self.nRot + 1, self.step):
            a = math.radians(i)
            # 计算参数i的每个值对应的x,y坐标
            x = R * ((1 - k) * math.cos(a) + l * k * math.cos((1 - k) * a / k))
            y = R * ((1 - k) * math.sin(a) - l * k * math.sin((1 - k) * a / k))
            self.t.setpos(self.xc + x, self.yc + y)
        # 完成绘制后隐藏光标
        self.t.hideturtle()

    def update(self):
        """一段一段绘制曲线来创建动画时所使用的绘图方法"""
        # 如果已完成，则跳过剩下的步骤
        if self.drawingComplete:
            return
        # 增加当前的角度
        self.a += self.step
        # 开始绘画
        R, k, l = self.R, self.k, self.l
        a = math.radians(self.a)
        x = self.R * ((1 - k) * math.cos(a) + l * k * math.cos((1 - k) * a / k))
        y = self.R * ((1 - k) * math.sin(a) - l * k * math.sin((1 - k) * a / k))
        self.t.setpos(self.xc + x, self.yc + y)

        # 如果绘制完成，设置drawingComplete标志并隐藏turtle光标
        if self.a >= 360 * self.nRot:
            self.drawingComplete = True
            self.t.hideturtle()

    def clear(self):
        """清除所有参数和图像"""
        self.t.clear()

四、实际应用

​ 物理源于生活，但生活不止是物理。这种将生活中的现象以及物理结构通过数学建模的方式来研究，可以有效的帮助我们处理很多问题。同时在这样一个信息化的时代里，利用信息技术来简化研究过程，也是一件非常奇妙的事情。

​ 想要在现实中制作一套独特的万花尺，这并不是一件难事。最简单的方案就是用一个饮料瓶盖放在双面胶的环里来模拟小圆的旋转过程，而我们只需要在这个瓶盖上打几个小孔，在不同的情况下将笔插进不同的小孔中即可。

​ 但是这种方案还有一个比较严重的问题：旋转的过程中有可能会打滑。如果打滑的程度较大，会严重影响绘制出来的图像的美感。面对这个问题，我们考虑增大瓶盖与外层环之间的摩擦力。不管是选用更粗糙的环的材质，还是在瓶盖表层涂上一层黏性物质，都可以有效的缓解这个问题。

方案的简单性必然会牺牲图像的准确性，所以如果想要绘制最完美的图像，还是考虑使用齿轮结构的万花尺吧！