特征工程 - 数据规约

一、基本介绍

　　Data Reduction

　　数据规约（数据缩减）是一种以更小的空间获得压缩版本或数据表示的方法，这种压缩数据保持了数据的完整性，并生成了与实际数据类似的分析。

　　这里不纠结数据规约的具体方法是如何分类的，只关注方法本身。

　　

二、降维

　　Dimensionality Reduction

　　下面4张图来源 → 《A Review of Dimensionality Reduction Techniques for Efficient Computation》

　　降维的一些优点：

 

　　降维的一些方法：

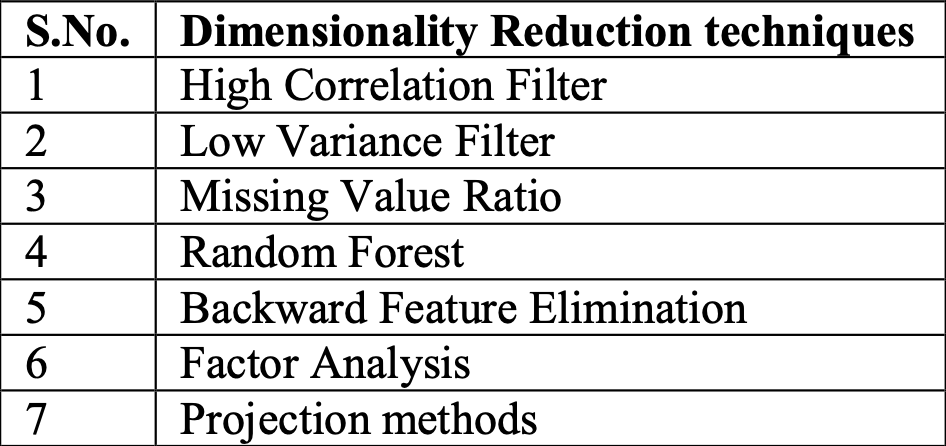
　　降维的基本方法主要分为两种：

1. 特征选择　　Feature Selection
2. 特征提取　　Feature Extraction

 

　　特征选择流程图：

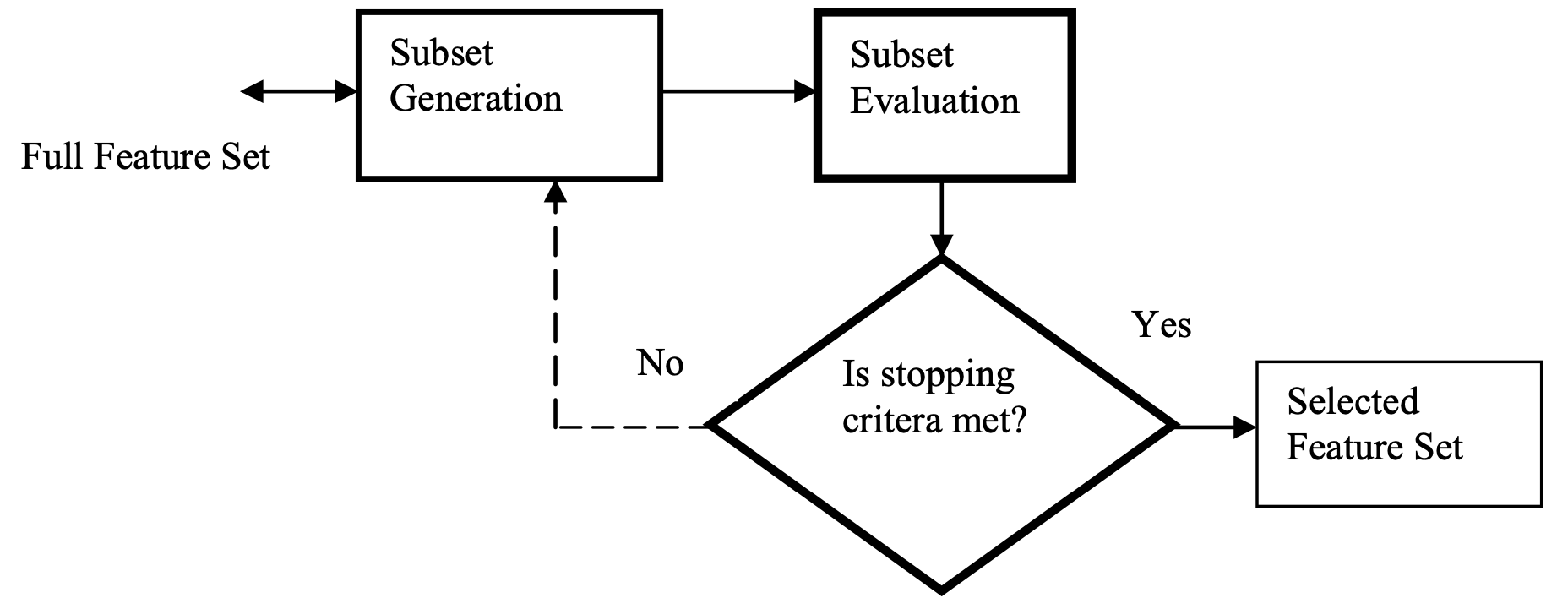
　　完整特征集 → 选择子集 → 评估 → 标准判断 → 结束/继续 

 

1、高相关性滤波

　　如果两个变量的相关系数很大，那么认为，这两个变量携带类似信息。

　　设定阈值，当相关系数超过阈值时，去掉其中一个即可。如：房屋面积用英尺和英寸表示时。

 

2、低方差滤波 

　　先将变量进行归一化，当变量方差足够小时，那么认为，这个变量携带的信息比较少少。

　　设定阈值，当变量的方差小于阈值时，去掉即可。如：吸烟室的数量对房价的影响（只有极个别的地方才会设置吸烟室）。

 

3、缺失值比率

　　计算变量含有缺失值的比例，当缺失率很大时，那么认为，这个变量所携带的信息比较少。

　　不过是否删除，需要根据具体情况而定。如：缺失值同时表示没有或未知，而不含缺失值的部分和目标变量的相关性又很大。

 

4、随机森林

　　随机森林是一种广泛使用的特征选择算法，它会自动计算各个特征的重要性，无需单独编程。这有助于选择较小的特征子集。

　　随机森林的优点：

1. 具有极高的准确率
2. 随机性的引入，使得随机森林不容易过拟合
3. 随机性的引入，使得随机森林有很好的抗噪声能力（能够更好的处理离群点）
4. 能处理很高维度的数据，并且不用做特征选择
5. 既能处理离散型数据，也能处理连续性数据，数据集无需规范化
6. 训练速度快，可以得到变量重要性排序
7. 容易实现并行化

　　随机森林的缺点：

1. 当随机森林中的决策树个数很多时，训练需要的空间和时间会很大
2. 随机森林的解释性很差

 

5、反向特征消除

　　以下是反向特征消除的主要步骤：

1. 先获取数据集中的全部n个变量，然后用它们训练一个模型。
2. 计算模型的性能。
3. 在删除一个变量后计算模型的性能（剩余几个变量循环几次），即我们每次都去掉一个变量，用剩余的n-1个变量训练模型。
4. 确定对模型性能影响最小的变量，把它删除。
5. 重复此过程，直到不再能删除任何变量。

 

6、因子分析

　　研究多个变量之间的内在联系，既隐变量，通过线性方法，将这些有内在联系的变量组合为新的变量，从而起到降维的效果。

　　步骤如下：

1. 对数据进行标准化处理。
2. 判断数据是否适合因子分析：KMO 和Bartlett 检验。
3. 选择因子个数，针对特定研究会有主观的选择个数，也可以根据特征根判断，进行个数选择。
4. 因子旋转。
5. 转变为新变量。

 

7、投影

　　在高维空间的数据，位于或接近低维子空间，将这些数据投影到该子空间。

 

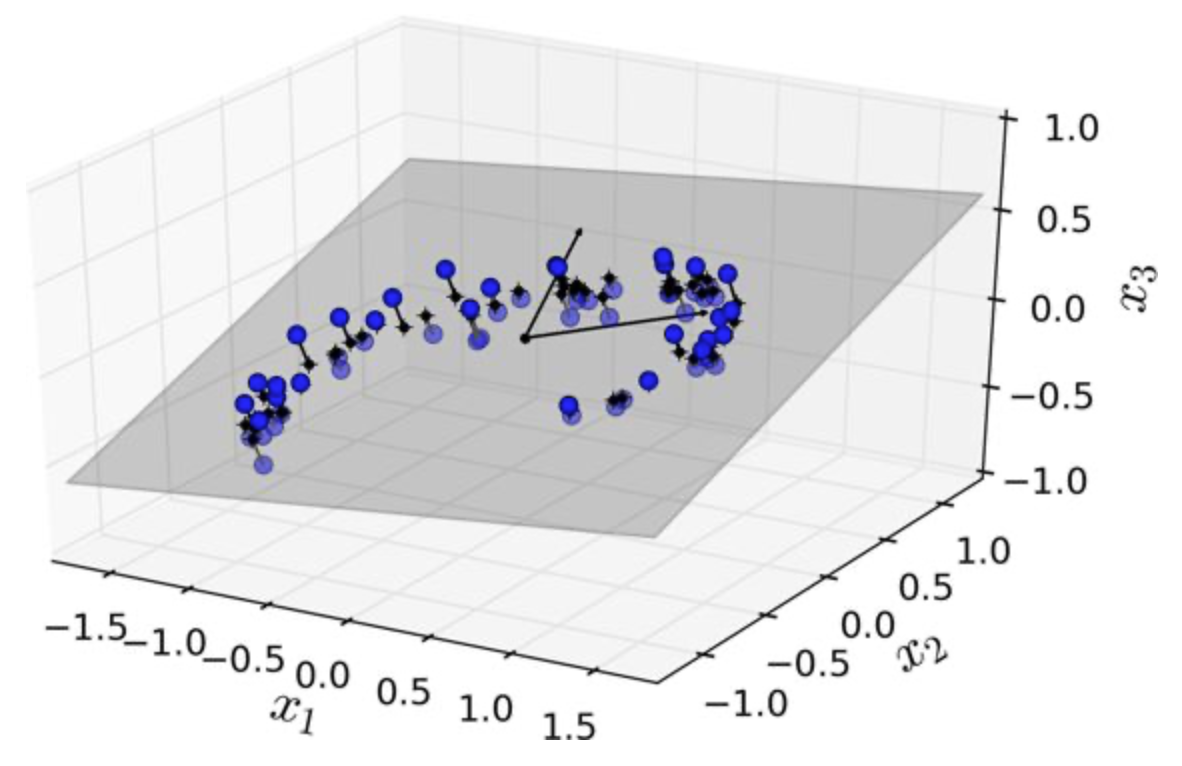
8、前向特征选择

　　前向特征选择其实就是反向特征消除的相反过程，即找到能改善模型性能的最佳特征，而不是删除弱影响特征。

　　步骤如下所述：

1. 选择一个特征，用每个特征训练模型，得到n个模型。
2. 选择模型性能最佳的变量作为初始变量。
3. 每次添加一个变量继续训练，重复上一过程，最后保留性能提升最大的变量。
4. 一直添加，一直筛选，直到模型性能不再有明显提高。

 

9、线性判别分析

　　LDA的思想是：最大化类间均值，最小化类内方差。意思就是将数据投影在低维度上，并且投影后同种类别数据的投影点尽可能的接近，不同类别数据的投影点的中心点尽可能的远。　　

 

10、独立成分分析 

　　最早应用于盲源信号分离（Blind Source Separation，BBS）。起源于“鸡尾酒会问题”：

　　在嘈杂的鸡尾酒会上，许多人在同时交谈，可能还有背景音乐，但人耳却能准确而清晰的听到对方的话语。这种可以从混合声音中选择自己感兴趣的声音而忽略其他声音的现象称为“鸡尾酒会效应”。

 　　如图所示，假设有3个麦克风，3个人同时说话。麦克风记录到3个人混合后的声音，ICA所要做的，就是通过收集到的数据，将混合声音分离成单个人的声音。

 

11、主成分分析

　　一组数据信息，用这组数据的主要部分表示它，忽略能提供较少信息的部分。用更小的维度，表示原数据的大部分（主要）信息。

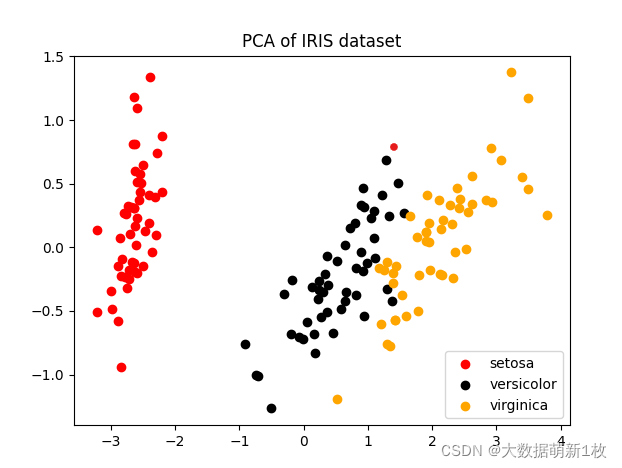
　　 如图，原数据是4维的鸢尾花数据集，通过PCA降至2维。

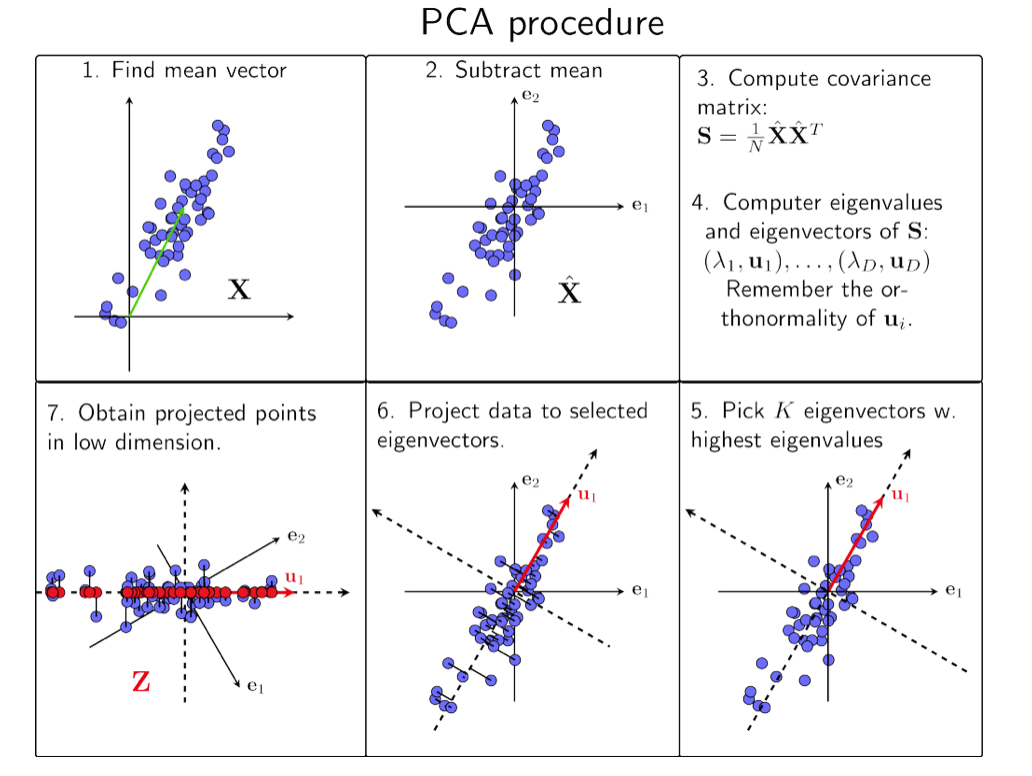
 　　如图，2维数据，通过PCA最终得到1维 数据，既左下角的红点。 

　　PCA步骤如下：

1. 将原始数据组成矩阵X。
2. 将X矩阵的每一行进行零均值化，即减去每一行的均值。
3. 求出X矩阵的协方差矩阵。
4. 求出协方差矩阵的特征值和特征向量，特征值就是每维元素的方差。
5. 将特征向量按对应特征值大小从上到下按行排列成矩阵，根据实际业务场景，取前k行组成矩阵P。
6. Y=PX即为降到k维后的目标矩阵。

 

12、广义判别分析

　　有别于LDA，GDA使用了核函数方法，处理非线性判别问题。

 

以上提到的12种降维方法外，还有许多其他的方法，如：核PCA、小波变换等等。

 

三、数值压缩

　　Numerosity Reduction

1、参数方法

　　下图来源 → https://cs.rhodes.edu/welshc/COMP345_F18/Lecture4.pdf

 　　简单的线性回归、多元回归和对数线性回归，利用原数据进行拟合后，保存函数模型的参数，再丢弃对应的数据（除可能存在的离群点）。

　　思考：如果存在离群点，应该怎么保存？保存包含对应样本？离群点应该在数据清洗时，就被删除掉了。

　　

2、非参数方法

　　Histogram、Clustering、Sampling、Data Cube Aggregation

• 直方图：

　　直方图方法就是分箱，将图中的bin个数由观测值的数量n减少到k个。从而使数据变成一块一块的呈现。bin的划分可以是等宽的，也可以是等频的。　

• 聚类　

　　将整个数据划分到不同的集群中，用数据的聚类表示代替实际数据，此外还有助于检测数据中的异常值。聚类的定义和算法也有多种选择。

• 抽样

　　抽样允许用更小的随机数据样本(或子集)表示大的数据集。

• 数据立方体聚类

　　可以参考这篇 → https://blog.csdn.net/forlogen/article/details/88634117

　　数据立方体的某个维度表示每个月的部分销售成绩，现在我们需要季度或者年度的成绩，那么就可以对这个维度进行总结。而数据以数据立方体的形式存储的，可以快速高效地实现总结。对数据立方体的基本操作，也就实现了数据缩减。

　　比如，上面链接中的江浙沪地区，就将江苏、浙江、上海这三个地区合并到了一起。

 

 

---