• 暂时无法获取
  • 人为遗漏
  • 设备等物理原因
  • 样本对象不具备该属性
  • 与分析的目标无关 
  • 获取代价太大
  • 系统实时性能要求较高

 

二、数据缺失机制

　　常将不含缺失值的变量称为完全变量，数据集中含有缺失值的变量称为不完全变量。
　　（变量又称维、特征、属性）

  • 随机缺失（missing at random，MAR）

　　　　含有缺失值的变量，和另一个变量相关，而导致缺失。

　　　　如：收入的缺失值和年龄相关，婴儿没有收入。

  • 完全随机缺失（missing completely at random，MCAR）

　　　　单纯的缺失，和任何变量都无关。 

  • 非随机缺失（missing not at random，MNAR）（或not missing at random，NMAR）

　　　　含有缺失值的变量，因为变量自身的原因，而导致缺失。

　　　　如：人们不愿透露的信息、难获取的信息。

 

三、缺失值处理的必要性

　　缺失值的影响

  • 使系统丢失大量有用信息
  • 系统中不确定性更加显著，确定性更难把握 
  • 空值的数据使挖掘过程陷入混乱，导致不可靠的输出 

 

　　数据挖掘算法本身更致力于避免数据过分拟合所建的模型，这一特性使得它难以通过自身的算法去很好地处理不完整数据。

　　因此，缺失值需要通过专门的方法进行推导、填充等，以减少数据挖掘算法与实际应用之间的差距。

 

四、缺失值的处理方法（待完善）

1、不处理缺失值（待完善）

　　不处理缺失值，直接使用包含缺失值的数据集。

　　其中包括： 贝叶斯网络、人工神经网络、随机森林等。 

　　贝叶斯网络提供了一种自然的表示变量间因果信息的方法，用来发现数据间的潜在关系。在这个网络中，用节点表示变量，有向边表示变量间的依赖关系。贝叶斯网络仅适合于对领域知识具有一定了解的情况，至少对变量间的依赖关系较清楚的情况。否则直接从数据中学习贝叶斯网的结构不但复杂性较高（随着变量的增加，指数级增加），网络维护代价昂贵，而且它的估计参数较多，为系统带来了高方差，影响了它的预测精度。人工神经网络也类似。

　　常见的能够自动处理缺失值的模型包括：KNN、决策树和随机森林、神经网络和朴素贝叶斯、DBSCAN（基于密度的带有噪声的空间聚类）等。这些模型对于缺失值的处理思路是：

  • 忽略，缺失值不参与距离计算，例如KNN。
  • 将缺失值作为分布的一种状态，并参与到建模过程，例如各种决策树及其变体。
  • 不基于距离做计算，因此基于值的距离做计算本身的影响就消除了，例如DBSCAN。

在数据建模前的数据归约阶段，有一种归约的思路是降维，降维中有一种直接选择特征的方法。假如我们通过一定方法确定带有缺失值（无论缺少字段的值缺失数量有多少）的字段对于模型的影响非常小，那么我们根本就不需要对缺失值进行处理。

因此，后期建模时的字段或特征的重要性判断也是决定是否处理字段缺失值的重要参考因素之一。

 

2、删除 

　　若变量的缺失值较多，覆盖率较低，且重要性较低，可以直接删除变量。 
　　（变量又称维、特征、属性）

  • 变量删除（variable deletion）

　　某变量的缺失值很多，且该变量对研究的问题不是很重要，可以考虑删除该变量。

　　这种做法减少了供分析用的变量数目，但没有改变样本数量。

  • 成对删除（pairwise deletion）（不推荐）

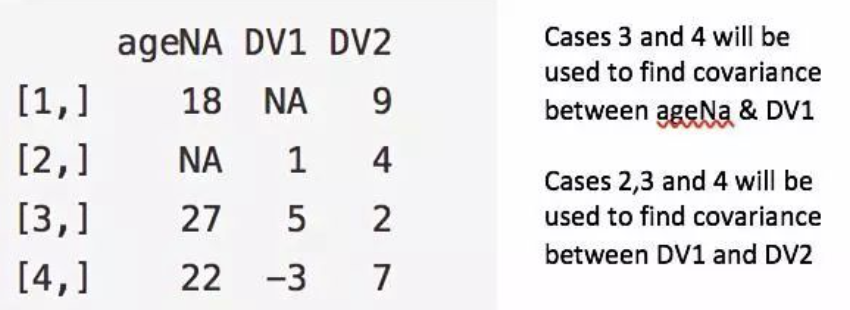
　　涉及变量之间的分析时，如果这个样本，需要进行分析的变量，含有缺失值，则删除。

　　只选取，进行分析的变量，没有缺失值的样本。

　　图中列举了 ageNA&DV1和 DV1&DV2两对例子，他们只是选取了完整样本集的两个不同子集进行分析。

　　优点：增强分析效果。 

　　缺点：假设缺失数据服从MCAR，最终模型的不同部分得到不同数量的观测值，模型解释非常困难。

  • 成列删除（listwise deletion）

　　删除含有缺失值的样本，只适合当样本的关键变量缺失，或含有缺失值的样本数占比很小的情况。

　　　　　　

3、插补（重点）

　　Imputation

（1）人工填写

　　Filling manually

　　当对手头的数据集足够了解时，可以选择手动填写缺失值。

　　费时，数据规模很大、缺失值很多的时候，该方法不可行，一般不推荐。

　　 

（2）特殊值填充

　　Treating Missing Attribute values as Special values

　　将缺失值作为一种特殊的属性值来处理，如所有的缺失值都用“unknown”填充。

　　一般作为临时填充或中间过程，有时可能导致严重的数据偏离，一般不推荐。 

 

（3）平均值/众数填充

　　Mean/Mode imputation

　　将初始数据集中的属性分为数值属性、非数值属性来分别进行处理。 

　　如果缺失值是数值型的，使用变量的非缺失值的平均值，填补缺失值。

　　如果缺失值是非数值型的，使用变量的非缺失值的众数，填补缺失值。

　　当然，根据情况，也有使用中位数进行填补的。　　

　　

　　使用众数填补参考 → 参考链接 ← 下图取自

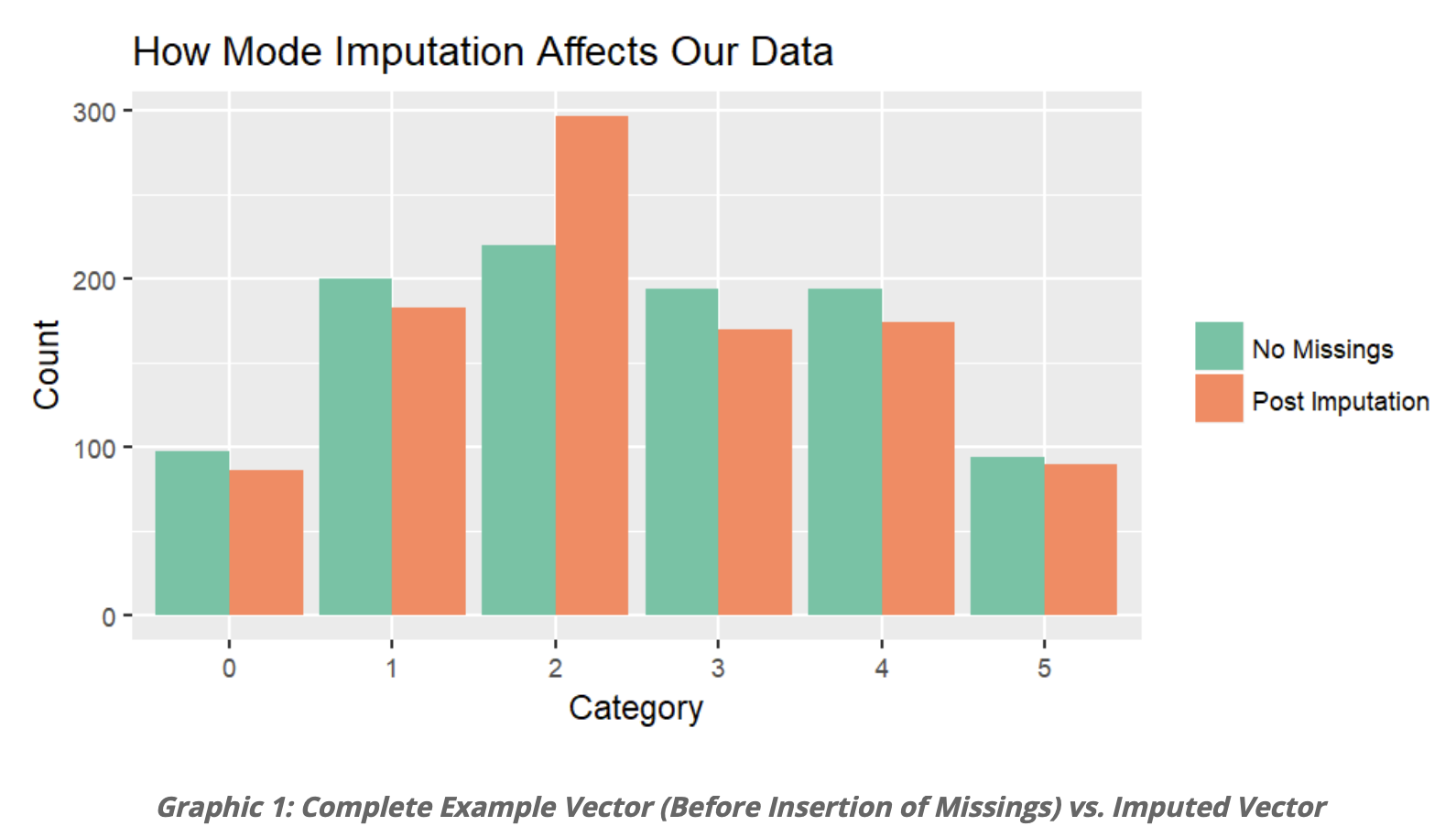
　　这张图展示了使用众数进行填补的效果。绿色是完整的无缺失值的数据集，在这个数据集上随机制造10%的缺失值，然后用众数进行填充，填充结果是橙色。很明显，使用众数填充缺失值，缺点是产生偏差。　

　　 
　　使用平均值填补参考 → 参考链接 ← 下图取自

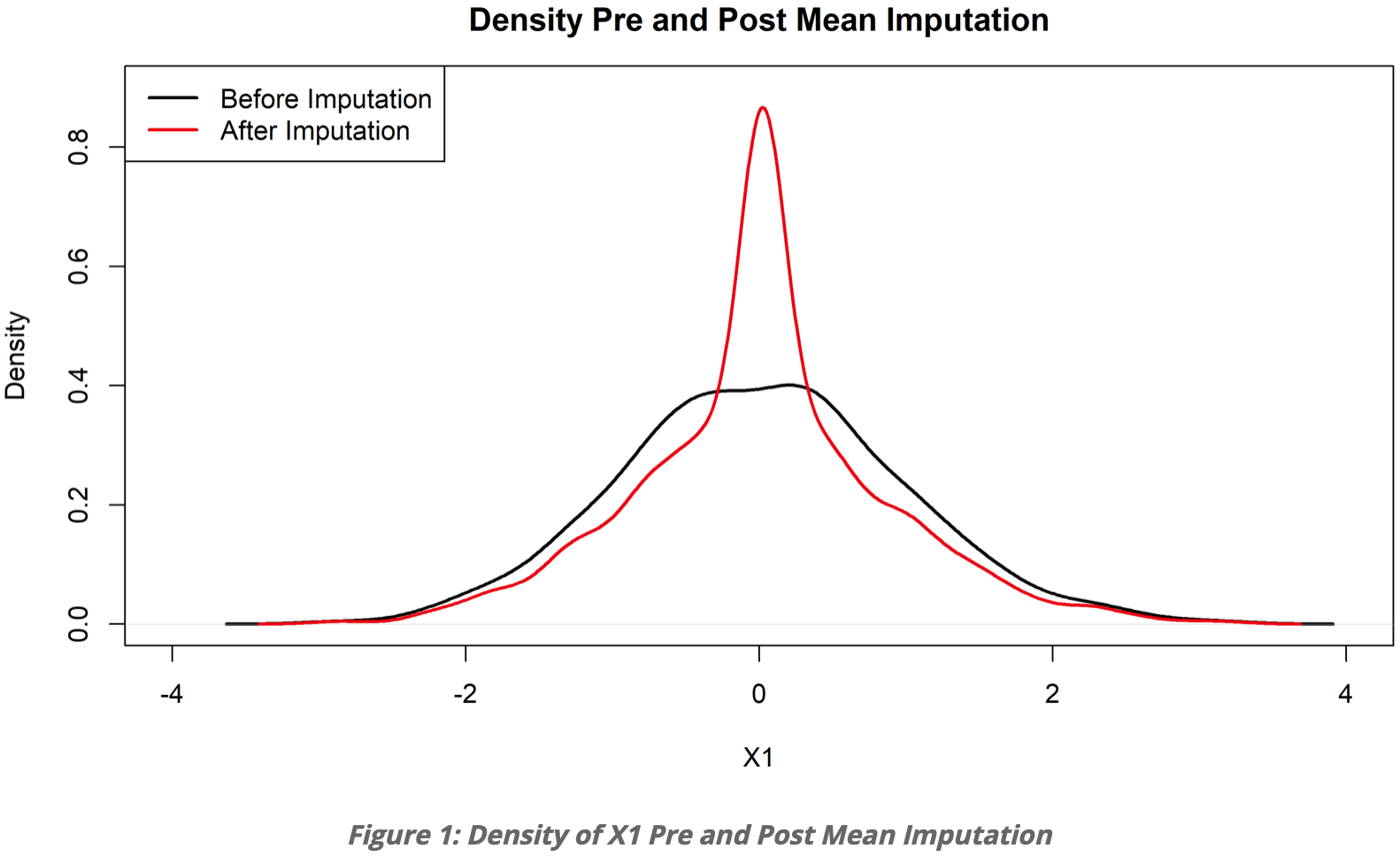
　　这张图展示了使用平均数进行填补的效果。黑色是有20%的值是缺失的，用平均值进行填充，填充结果是红色。很明显出现了一个很奇怪的峰，使用平均值填充缺失值，缺点是产生偏差。

　　

　　优点：

　　1、不会减小的样本总量。

　　2、便于理解，操作简单。

　　3、如果机制是MCAR，则样本均值是无偏的，所以用平均值代替缺失值是有效的方法。

 　　

　　缺点：

　　1、导致变量间的相关性分析和回归系数，趋于0。

　　2、导致置信区间缩小。

　　3、如果是MAR或MANR机制，那么用来填充的的平均值是有偏的。

 

（4）热/冷卡填充

　　Hot/Cold Deck imputation → 详细讲解连接

　　热卡填充：在完整数据中找到一个与它最相似的样本，用这个样本对应的属性值，填充缺失值。

　　冷卡填充：通过其他数据集找到能填充缺失部分的值。如：去年同季度的数据，填补本年同季度的缺失值。或不同机构对统一问题的调查数据。

　　当使用距离进行相似判断时，可以看做是KNN的一种特殊情况，KNN是参考的是K个，而热卡填充参考的是最近的1个，所以热卡填充可以用KNN做。 　　

 

　　根据问题，选用不同的标准来对相似进行判定。缺点在于难以定义相似标准，找到相似样本，选择标准时的主观因素较多。 

 

（5）K近邻法

　　K-nearest neighbors

　　根据距离或相关性分析，找到离含有缺失值的样本 最近的K个样本，将这K个值加权平均来估计该样本的缺失值。 

  • 数值　　使用欧氏距离、曼哈顿距离等或余弦相似性等。
  • 分类　　汉明（Hamming）距离。对于分类属性，若两个样本的值不同，则距离加一。汉明距离实际上与属性间不同取值的数量一致。 

　　优点：易理解、易实现，其非参数的特性在某些数据非常“不寻常”的情况下非常有优势。 

　　缺点：分析大型数据集非常耗。在高维数据集中，最近与最远邻居之间的差别非常小，KNN的准确性会降低。 

 

（6）使用所有可能的属性值填充

　　Assigning All Possible values of the Attribute

　　参考论文 《On the Unknown Attribute Values in Learning from Examples》

　　如果属性值缺失，那么使用该属性的所有可能值进行填充。如：颜色值缺失，那么用所有的n个颜色进行填充。一个样本变成了n个样本。

　　但是，当数据量很大或者缺失的属性值或个数较多时，其计算的代价很大，可能的测试方案很多。如：一个样本的属性A和属性B同时缺失，那么填充的数量等于，属性A的可能值个数n，属性B的可能值个数m，相乘得mn个样本。

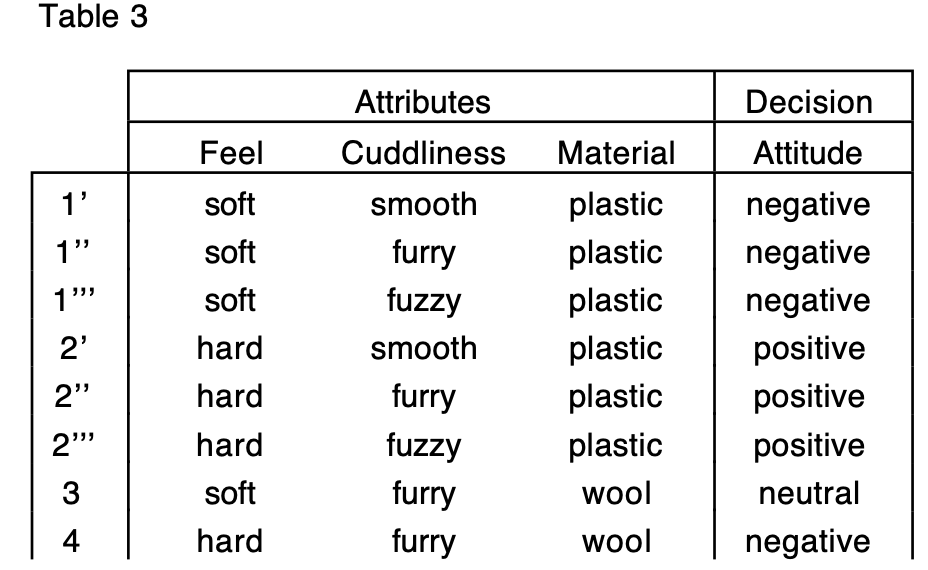
 　　图片来自论文，表1填充后得到表2。

 

　　缺点：适合较小的数据集，数据量很大或含缺失值的属性值数量较多时，计算代价很大，一般不推荐。 

 

（7）回归

　　Regression　　

　　一个数据集，预测值Y和属性X、Z，其中X含有缺失值。使用不含缺失值的样本组成完整的数据集，建立回归方程或回归算法，有些具体问题可能会有指定的方程，如：Capital Asset Pricing Model (CAPM)。将已知的Y值带入求解缺失的X，进行填充。当变量不是线性相关时会导致有偏差的估计，较常用。 

　　但是要注意！！！ 防止过拟合！！！

 

　　下面介绍三种不同类型的回归进行imputation：　　

　　Deterministic regression imputation

　　Stochastic regression imputation　　

　　Predictive mean matching　　

 

  • 使用Stochastic vs Deterministic 填补参考 → 链接 ← 下图取自

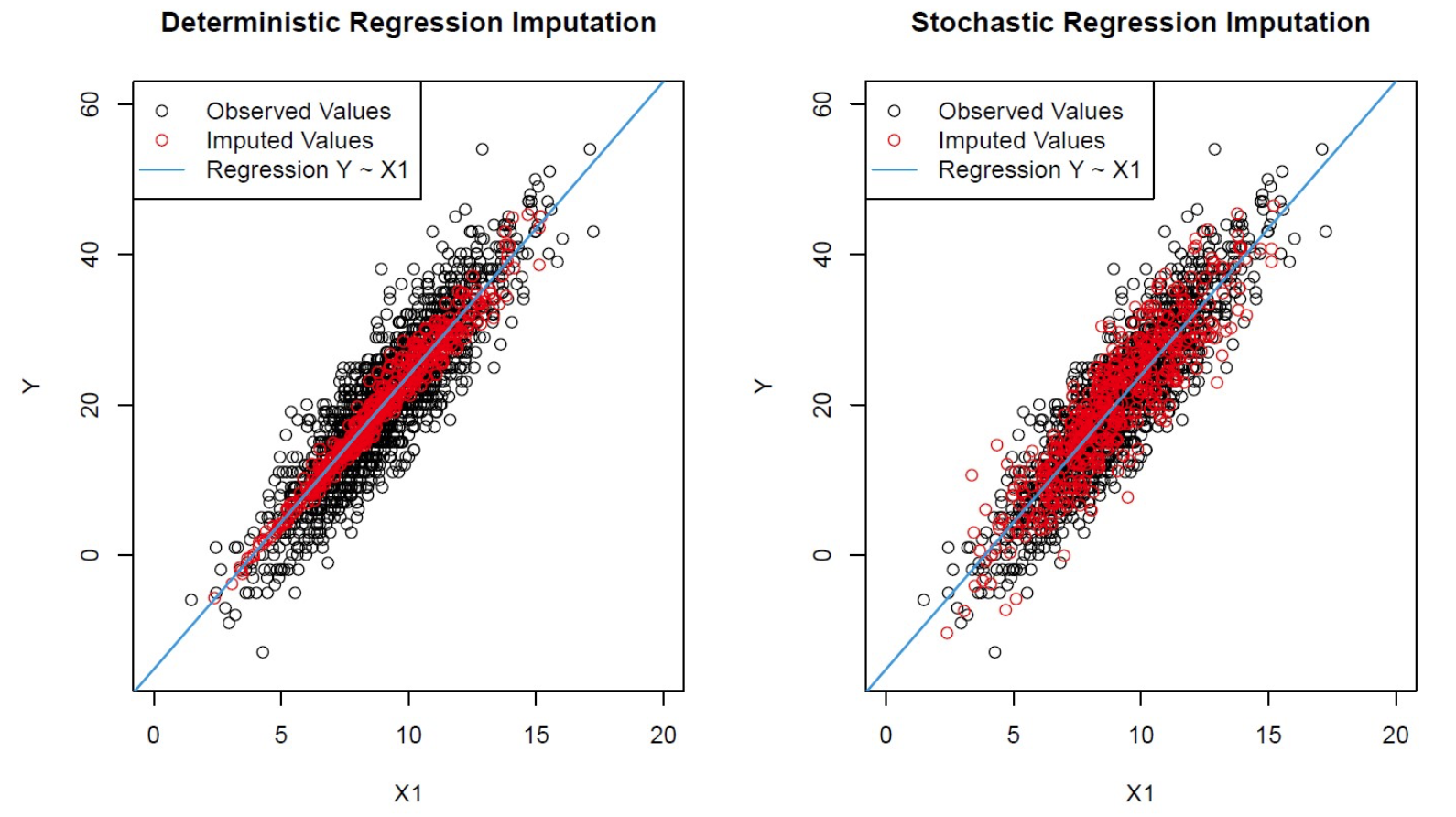
 　　对比填补缺失值后的相关性。

　　0.897是完整数据集的相关系数，0.912是使用Deterministic 方法的相关系数，0.894是使用Stochastic 方法的相关系数。

　　综上，Stochastic 引入的偏差更小。　　

 

 

　　缺点：1、随机回归可能会引入不合理的值，比如收入的缺失值可能填补为负数。

　　　　　2、当数据是异方差时，随机回归归算会导致较差的结果。随机回归假设随机误差平均具有相同的大小，通常会导致输入值的随机误差项过小或过大。如下图所示。

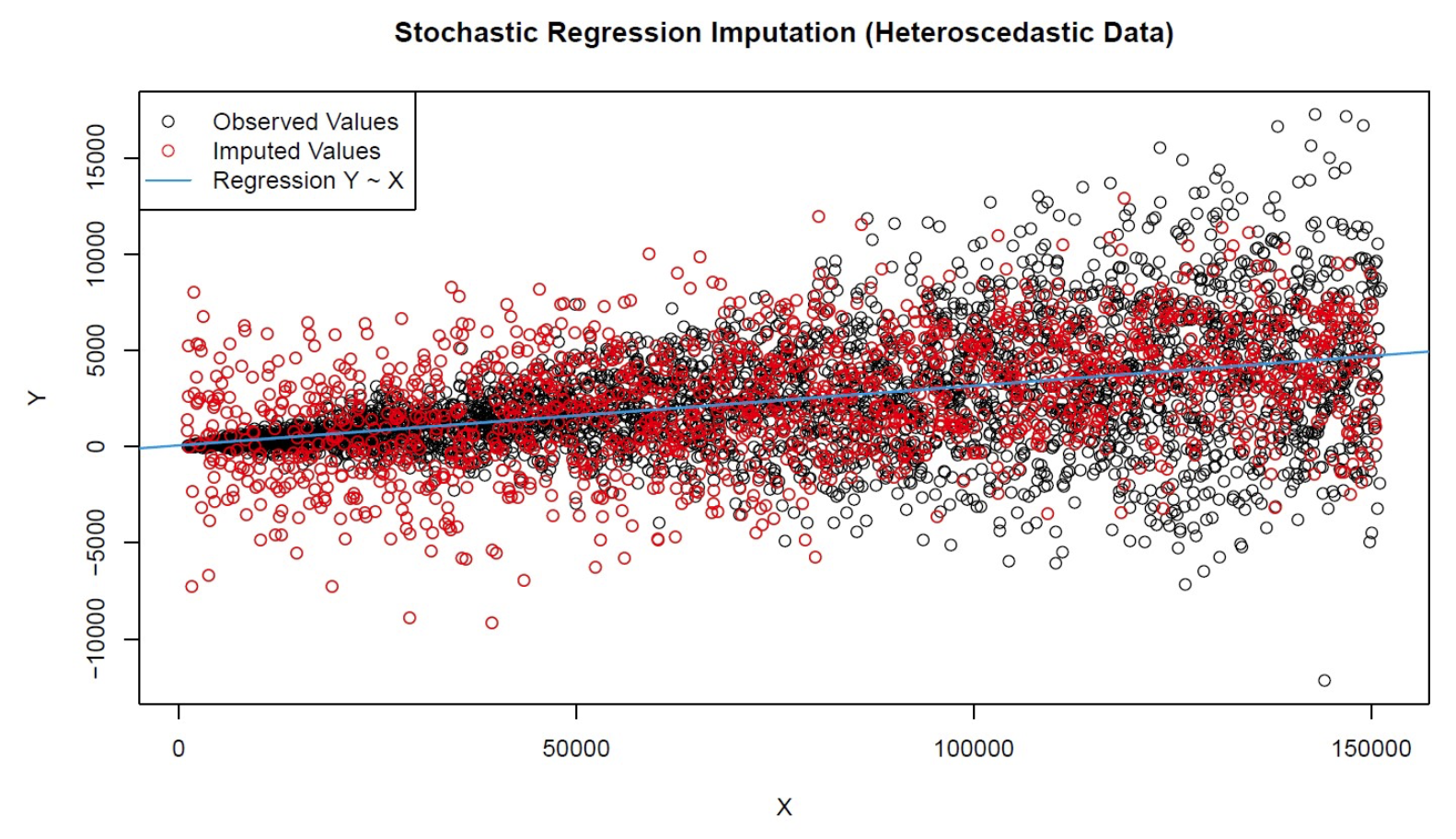 　　当数据是异方差时，使用Stochastic 进行填补。可以发现，Y的方差是随X的增大而增大的，而填补的缺失值的方差却是不变的，所以Stochastic 方法只适用于非异方差的变量。

 

  • 使用Predictive mean matching 填补参考 → 链接 ← 下图取自

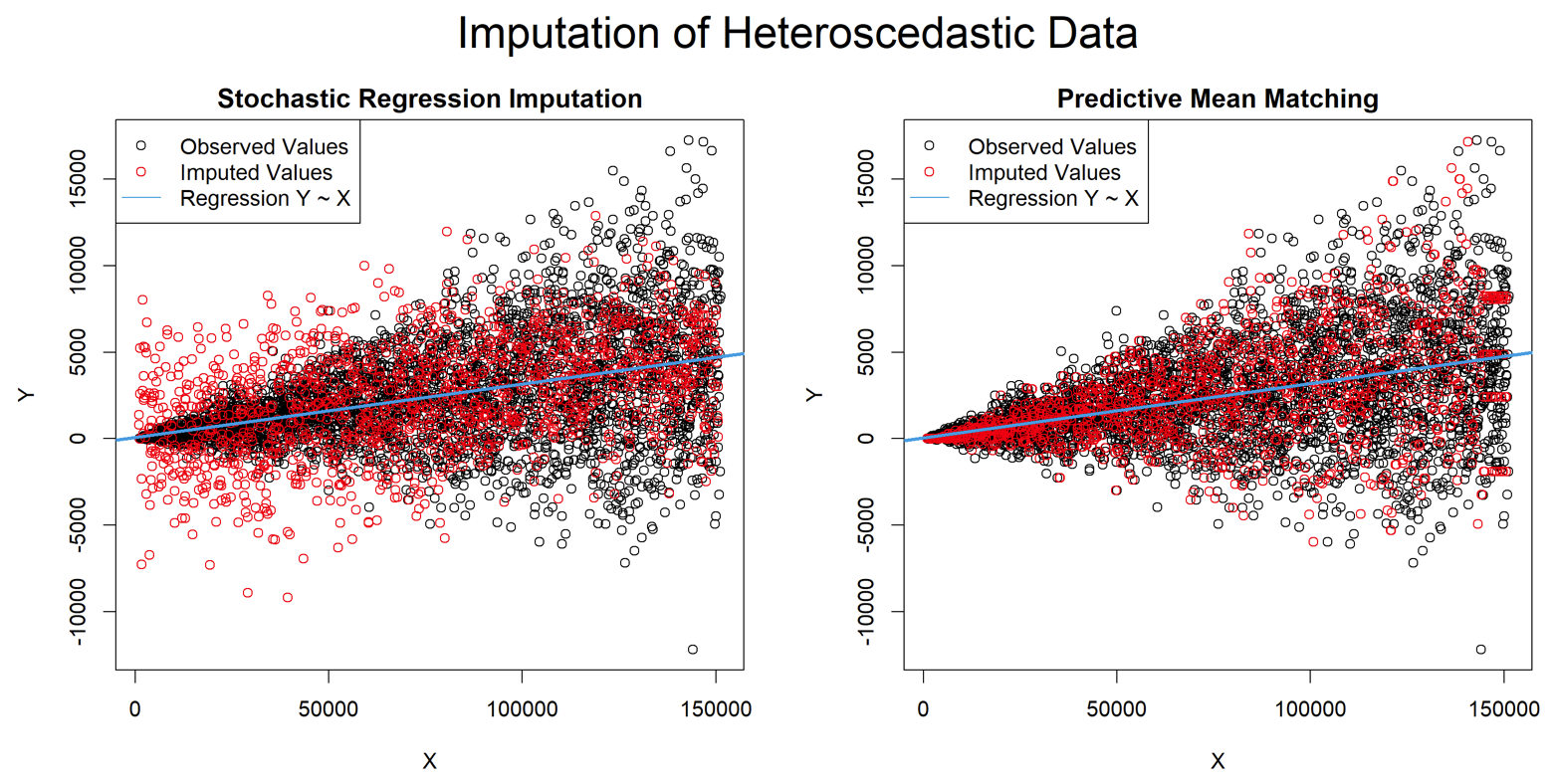
 　　Stochastic 方法和Predictive mean matching 方法对比。很直观，当数据是异方差时，Predictive mean matching方法效果更好，更加贴合完整数据集的分布。该方法只计算实际观察到的值，因此，插入值的范围总是介于观测值的最小值和最大值之间。

 　　

（8）期望值最大化方法（待完善）

　　Expectation maximization，EM

　　EM算法是一种在不完全数据情况下计算极大似然估计或者后验分布的迭代算法。

　　该方法可能会陷入局部极值，收敛速度也不是很快，并且计算很复杂。 

 

（9）多重插补（待完善）

　　Multiple Imputation，MI

　　多重插补分三个步骤： 

　　（1）插补：将不完整数据集缺失的观测行估算填充m次，填充值是从某种分布中提取的。更好的方法是采用马尔科夫链蒙特卡洛模拟（MCMC，Markov Chain Monte Carlo Simulation），这一步骤将生成m个完整的数据集。 

　　（2）分析：分别对每一个（m个）完整数据集进行分析。 

　　（3）合并：对来自各个填补数据集的结果进行综合，产生最终的统计推断，这一推断考虑到了由于数据填补而产生的不确定性。该方法将空缺值视为随机样本，这样计算出来的统计推断可能受到空缺值的不确定性的影响。

 

（10）C4.5方法（待完善）

　　通过寻找属性间的关系来对遗失值填充。它寻找具有最大相关性的两个属性，其中没有遗失值的一个称为代理属性，另一个称为原始属性，用代理属性决定原始属性中的遗失值。这种基于规则归纳的方法只能处理基数较小的名词型属性。 

 

（在上述方法中，比较推荐是的多重插补和回归。针对某项特征数据大量缺失时，随机森林回归十分有效；当数据存在明显的线性关系时，线性回归也有很好的效果。）

 

（11）哑变量调整

　　Dummy Variable Adjustment 

　　这是一种在回归分析中处理预测变量缺失数据的方法，它适用于任何类型的回归。

　　设置一个单独的变量，专门表示另一个变量是否含有缺失值，缺失设为0，存在设为1。同时，在原变量的缺失值处，填上c（可以是任何常数）。

　　随后，进行回归。这种调整的好处是它利用了所有可用的缺失数据的信息（是否缺失）。为了便利，一般c的设置为现有非缺失数据的均数。

　　但这种方法会产生不可忽视的偏差估计，在这篇论文中提到。

　　当然也有人提出了两种特殊情况，可以参考这篇文章。

　　对此方法需求不足，不深入。