正则化L1 和L2 和Elastic Net（待更）

一、什么是正则化

　　英文 Ragularization

　　使模型普通化、均匀化、一般化，防止或减小 模型的过拟合。

二、正则化项（惩罚项）

　　英文 Ragularizer（Penalty）

　　经验风险 -- 经验指模型的预测值和数据真实值的相近程度

　　结构风险 -- 结构指模型，当数据量偏少时，复杂结构的模型存在过拟合风险

三、具体内容

　　正则化项可以是模型参数的范数，这里只介绍一范数的L1 和二范数的L2。

　　1、L1 -- Lasso

　　　　一范数L1，实际是模型参数的绝对值，然后求和：

　　　　　　$$\sum_{i} | w_i|  $$

　　　　其中 $ w_i $ 是模型的参数。

　　　　以2 维为例，模型参数为$ w_1 $，$ w_2 $。

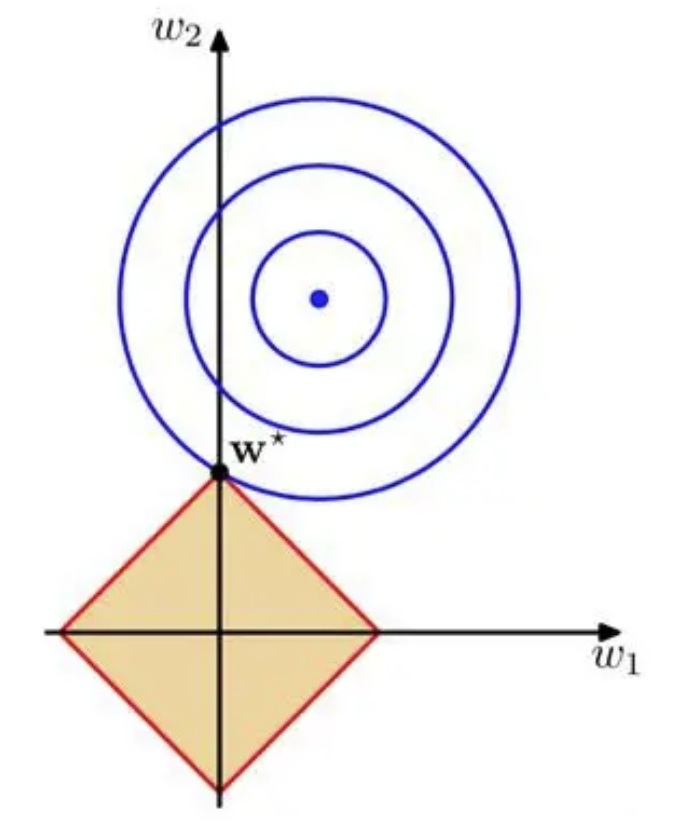
　　　　蓝色 -- 损失函数，中心最小

　　　　黄色 -- L1，红线内为允许范围

　　　　多数情况下，黄色区域的顶点处，取到最优解$w^* $。而顶点都是在轴上的，代表有的模型参数为0，所以L1 可以进行特征选择。

　　2、L2 -- Ridge

　　　　二范数L2，实际是模型参数的平方，然后求和：

　　　　　　$$\sum_{i} w_i^2  $$

　　　　以2 维为例，模型参数为$ w_1 $，$ w_2 $。

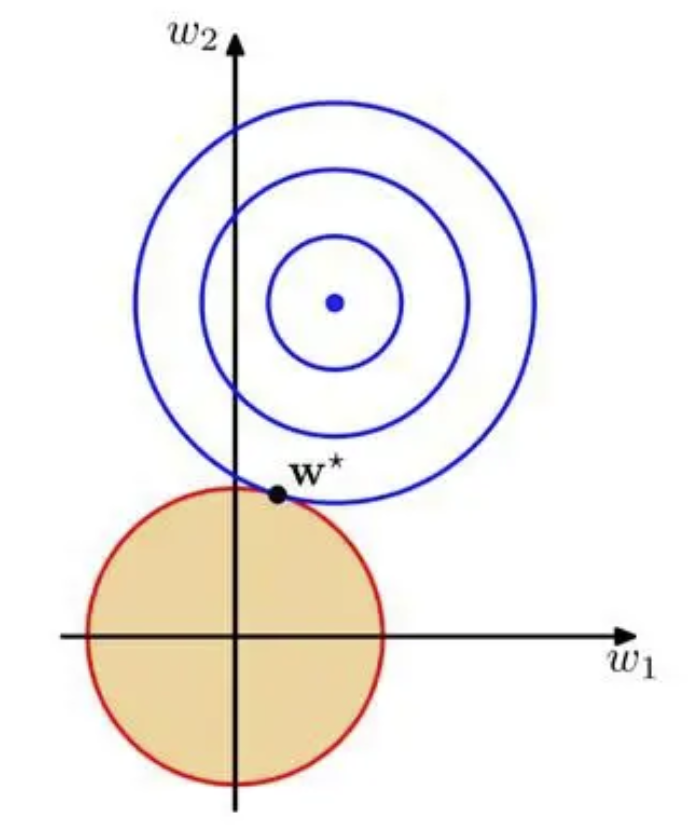
　　　　黄色区域的边缘处，均有可能取到最优解$w^* $。最优解不被限制在轴上，模型参数都可取到值，所以L2 可以分散特征，同时表现特征的重要程度。 

　　3、L1 + L2 -- Elastic Net

　　　　Paper ← 论文链接

　　　　（1）原始Elastic Net

　　　　　　公式（3）是损失函数。

　　　　　　公式（4）是最优解。

　　　　　　公式（5）是公式（3）的构建过程：原最小二乘 + 约束项

 　　　　　　我们称 约束项 为 elastic net penalty。

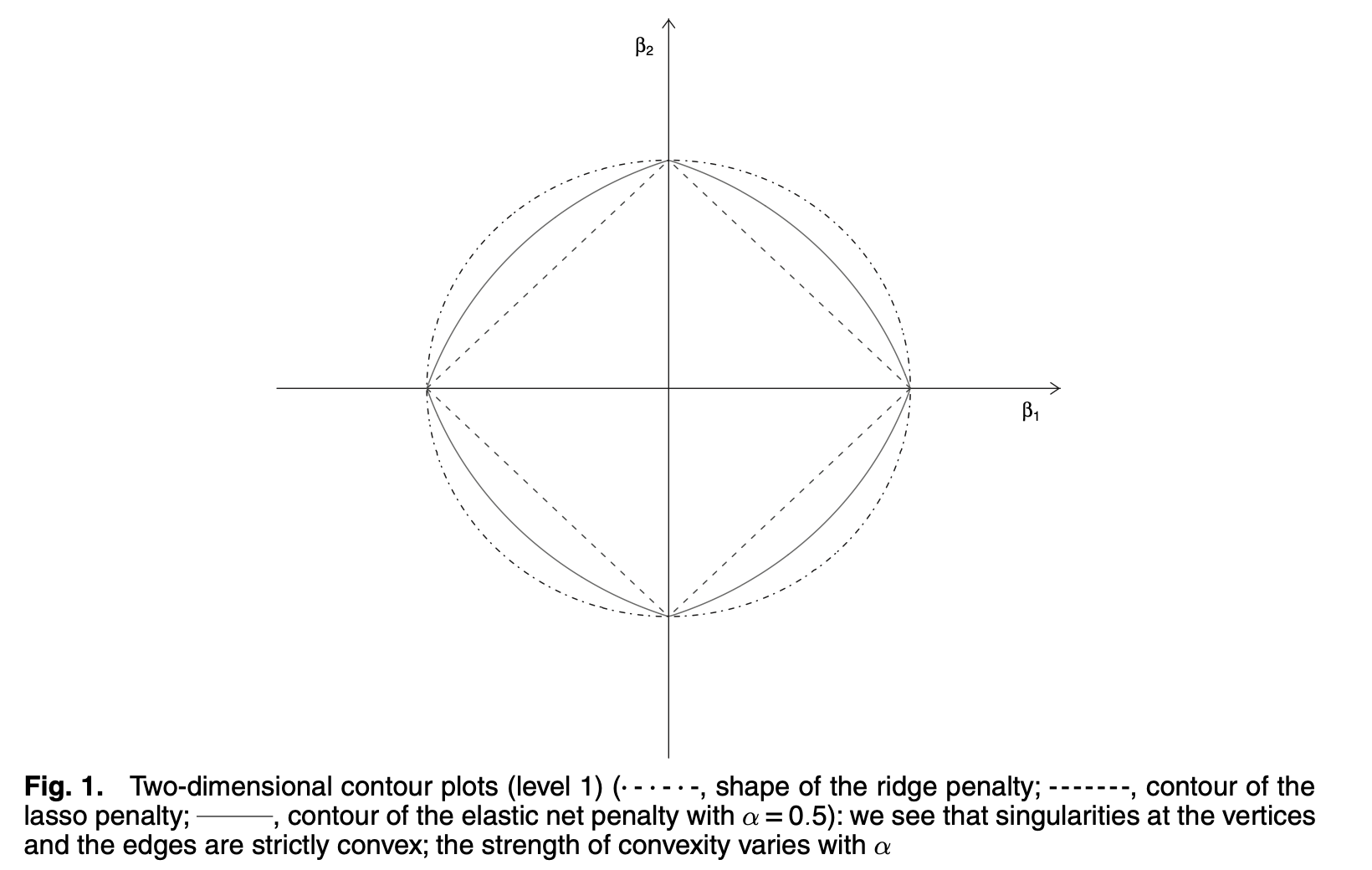
 　　　　　　$ \alpha $就是调节Lasso 和Ridge 的两者占比程度。

　　　　（2）Elasitc Net（待更）