IoU 交并比

一、IoU(Intersection Over Union，交并比)

　　intersection 交集

　　over 在……之上

　　union 并集

 

　　　　$IoU = {|A\cap B| \over |A\cup B|}$

 

　　在目标检测领域中，IoU用来衡量检测框的交叠程度，既，预测的框和真实的框的交叠率。

　　理想情况为 $IoU = 1$，既两个框完全重合。

　　如果 $IoU \gt 0.5$，则视为检测正确，检测结果可以接受。

　　0.5这个值可以根据个人需要进行调节，一般设置在0.5到1之间，值越大表示越精确。

 

二、IoU的计算

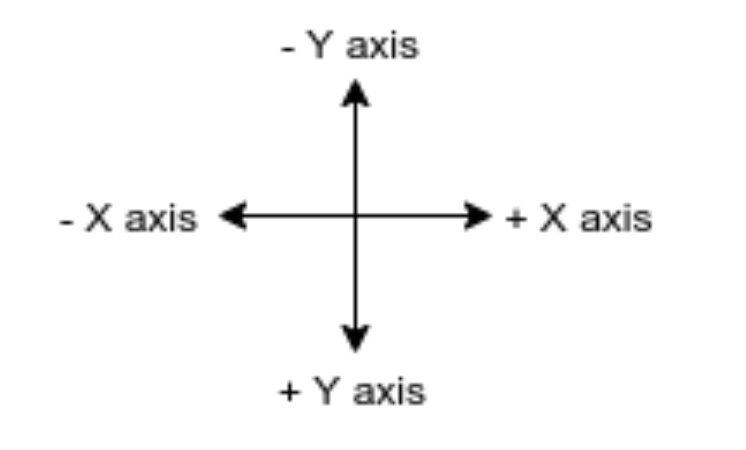
　　参考坐标系

 

　　检测框

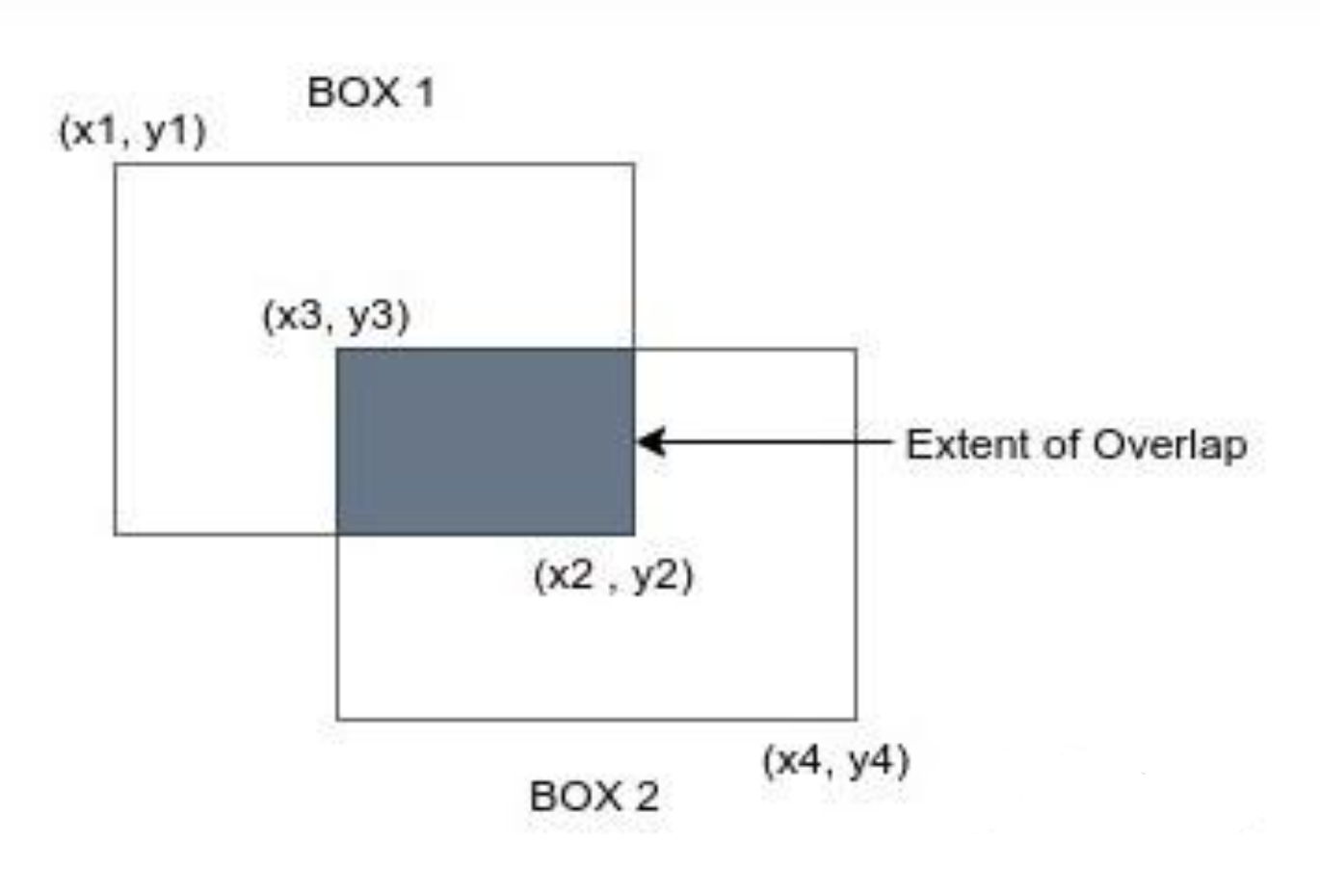
　　计算目标

　　　　已知BOX1 的顶点(x1，y1)(x2，y2)和BOX2 的顶点(x3，y3)(x4，y4)

1. 1. BOX1 和BOX2 的交集部分，既阴影部分
   2. BOX1 和BOX2 的并集部分，既BOX1面积 + BOX2面积 - 阴影部分

　　　　容易求解部分：BOX1面积和BOX2面积

　　　　　　根据BOX顶点，求得长和宽，相乘即得面积。

　　　　困难求解部分：阴影部分

　　　　　　根据参考坐标系可知，X轴的正方向为右，Y轴的正方向为下。

• • • 阴影部分左上角顶点：

　　　　　　　　　　$x_{阴影左上}:max(x1，x3)$　　　　$y_{阴影左上}:max(y1，y3)$

• • • 阴影部分右下角顶点：

　　　　　　　　　　$x_{阴影右下}:min(x2，x4)$　　　　$y_{阴影右下}:min(y2，y4)$

• • • 根据阴影部分的左上角顶点和右下角顶点，可得阴影部分的高和宽：

　　　　　　　　　　高：$H_{阴影} = y_{阴影右下} - y_{阴影左上} = min(y2，y4) - max(y1，y3)$

　　　　　　　　　　宽：$W_{阴影} = x_{阴影右下} - x_{阴影左上} = min(x2，x4) - max(x1，x3)$

• • • 得到阴影部分的面积为：

　　　　　　　　　　$S_{阴影} = H_{阴影} * W_{阴影} $

　　　　　　　　关键：

　　　　　　　　　　当BOX1 和BOX2 不重叠时，根据坐标轴方向，抽象表达4个顶点的关系：

$(x1，y1)\lt (x2，y2)\lt (x3，y3)\lt (x4，y4)$

　　　　　　　　　　当BOX1 和BOX2 重叠时，同理抽象表达4个顶点的关系：

$(x1，y1)\lt (x3，y3)\lt (x2，y2)\lt (x4，y4)$

　　　　　　　　　　发现，当不重叠时， $H_{阴影} \lt 0， W_{阴影} \lt 0$。此时重叠面积是0。

　　　　　　　　　　当重叠时，$H_{阴影} \gt 0， W_{阴影} \gt 0$。

• • • 根据关键进行调整，阴影部分的高和宽为：

　　　　　　　　　　高：$H_{阴影} = max(0，y_{阴影右下} - y_{阴影左上}) = max(0，min(y2，y4) - max(y1，y3))$

　　　　　　　　　　宽：$W_{阴影} = max(0，x_{阴影右下} - x_{阴影左上}) = max(0，min(x2，x4) - max(x1，x3))$

　　代码参考

def iou(box1, box2):
    '''
    两个框(二维)的 iou 计算，边框以左上为原点。
    box1:[x1,y1,x2,y2]，依次为左上顶点和右下顶点坐标
    box2:[x3,y3,x4,y4]
    '''
    h = max(0, min(box1[3], box2[3]) - max(box1[1], box2[1]))
    w = max(0, min(box1[2], box2[2]) - max(box1[0], box2[0]))
    area_box1 = ((box1[2] - box1[0]) * (box1[3] - box1[1]))
    area_box2 = ((box2[2] - box2[0]) * (box2[3] - box2[1]))
    inter = w * h
    union = area_box1 + area_box2 - inter
    iou = inter / union
    return iou

三、IoU作为损失函数

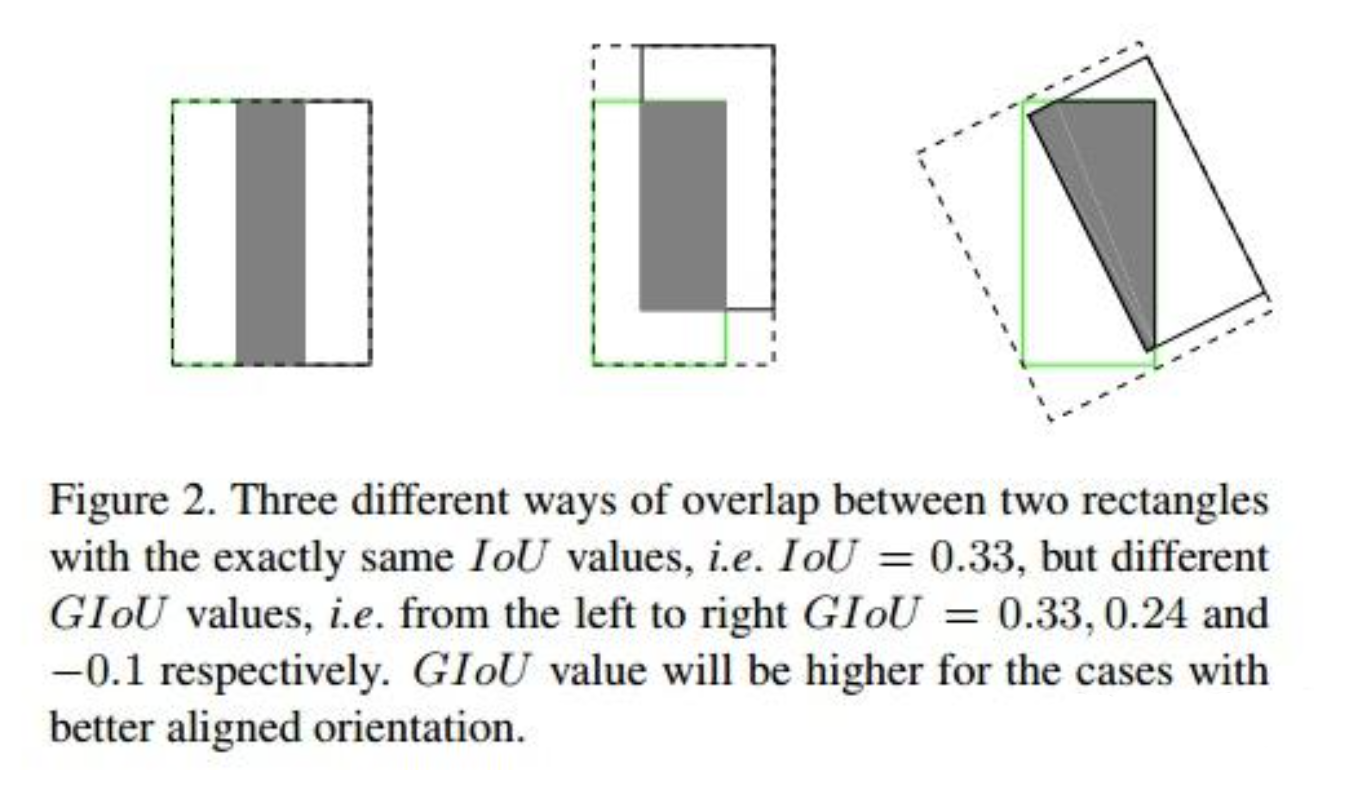
　　如图，三种情况下的IoU 值相同，但我们更倾向于第一种情况。IoU 作为损失函数时，不一定得到第一种情况。

　　IoU 不存在学习训练，只是单纯地计算重叠率。

 

待拓展 GIoU、DIoU、CIoU、YOLO。