sturges算法 根据sturges算法计算得到的适合的分布区间

 

▷ 斯特吉斯规则：公式、示例和计算器 https://statorials.org/cn/%e6%96%af%e7%89%b9%e5%a5%87%e6%96%af%e8%a7%84%e5%88%991/

斯特奇斯法则

经过 本杰明·安德森博 8月 5, 2023 统计数据

本文解释了什么是斯特奇斯规则及其公式。您还将找到斯特奇规则的分步具体示例，以及在线斯特奇规则计算器。

斯特奇斯法则是什么？

斯特吉斯规则是用于计算数据集应划分的理想类数或区间数的规则。

斯特吉斯规则的公式指出，类的数量等于一加上数据总数的以 2 为底的对数。

 

c=1+\log_2(N)

 

金子

 

c

是班级或间隔的数量，

N

是样本中观测值的总数。

大多数计算器只允许以 10 为底的对数进行计算。在这种情况下，您可以使用以下等效公式：

Ezoic
  1. x
     
    1. Now Playing
       
    2.  
    3.  
    4.  
    5.  
    6.  
    7.  
    8.  
    9.  
    10.  

 

c=1+\cfrac{\log(N)}{\log(2)}

斯特奇规则是由德国统计学家赫伯特·斯特奇于 1926 年创建的。

斯特吉斯规则的示例

现在我们知道了斯特奇斯规则是什么，我们将通过解决逐步练习来了解如何使用统计中的斯特奇斯规则来计算数据集的间隔。

  • 测量了50个不同人的样本量，所有值都记录在下面的数据表中。应用斯特吉斯规则将数据集划分为多个区间，然后将数据绘制在直方图上。

首先，我们需要将数据分成区间。总共有 50 个数据元素，因此我们使用 Sturges 规则与此值：

 

\begin{array}{l}c=1+\log_2(N)\\[2ex]c=1+\log_2(50)\\[2ex]c=1+5,64\\[2ex]c=6,64\\[2ex]c\approx 7\end{array}

 

因此，有必要将数据分开并将它们分为七个区间。我们现在需要知道每个区间的宽度，为此，只需将最大值减去最小值除以区间总数：

 

a=\cfrac{\text{valor m\'aximo}-\text{valor m\'inimo}}{c}=\cfrac{205-145}{7}=8,57\approx 9

 

简而言之，振幅为9的区间必须有7个，因此使用Sturges方法计算出的区间为：

 

[145,154)

 

[154,163)

 

[163,172)

 

[172,181)

 

[181,190)

 

[190,199)

 

[199,208)

 

计算完区间后，我们需要统计某个数据在每个区间出现的次数，并构建频数表：

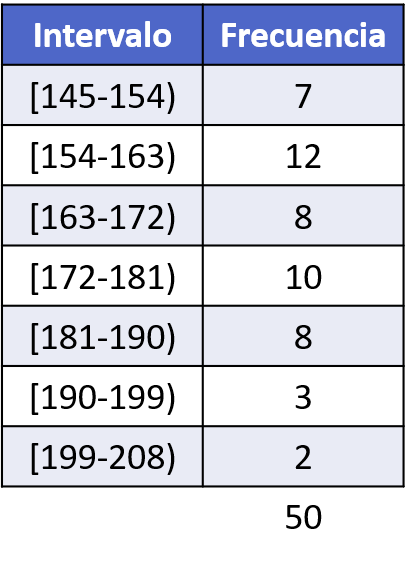
最后，从频率表中，我们可以创建直方图来绘制数据：

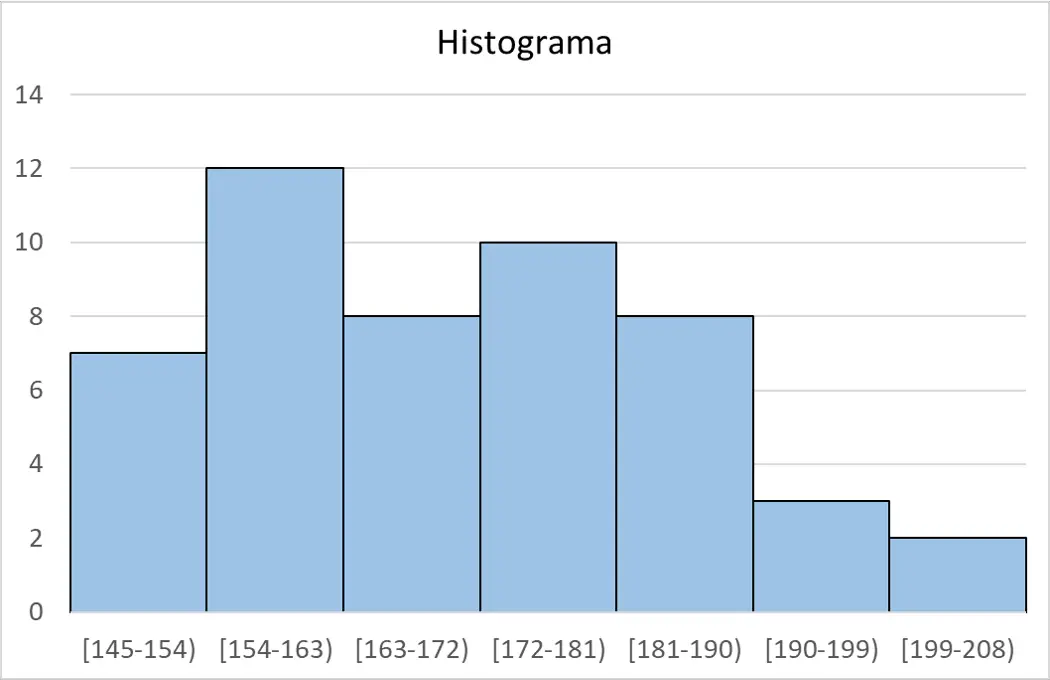
斯特吉斯规则直方图、统计
➤请参阅：如何制作直方图

斯特奇斯规则计算器

输入数据样本总数，点击“计算”，计算器将返回根据Sturges规则计算出的区间数。

  • 数据总数 = 

默认分组为系统自动根据sturges算法计算得到的适合的分布区间。点击分布区间下拉菜单上的删除按钮，可以恢复为默认分组。

 

分布分析--增长分析（私有化）-火山引擎 https://www.volcengine.com/docs/6285/65945

 

什么是斯特奇斯规则？ （定义和示例）- Statorials https://statorials.org/cn/%e6%96%af%e7%89%b9%e5%a5%87%e6%96%af%e8%a7%84%e5%88%99/

 

 

种帮助我们可视化一组数据中值的分布的图表。

事实证明，直方图中使用的方框数量会对我们解释数据的方式产生巨大影响。

如果我们使用的组太少，数据中真正的底层模式可能会被隐藏：

如果我们使用太多组，我们可以简单地可视化数据集中的噪声：

幸运的是，我们可以使用一种称为斯特吉斯规则的方法来确定直方图中使用的最佳框数。

斯特吉斯规则使用以下公式来确定直方图中使用的最佳组数：

最佳 bin = ⌈log 2 n + 1⌉

金子：

  • n：数据集中的观测总数。
  • ⌈ ⌉：表示“上限”的符号，即将答案四舍五入到最接近的整数。

示例：斯特吉斯规则

假设我们有以下数据集，总共有 n = 31 个观测值：

我们可以使用斯特吉斯规则来确定用于在直方图中可视化这些值的最佳框数：

最佳 bin = ⌈log 2 (31) + 1⌉ = ⌈4.954 + 1⌉ = ⌈5.954⌉ = 6 。

根据 Sturges 规则，我们应该在直方图中使用 6 个箱来可视化该值的分布。

对于该数据集，包含 6 个组的直方图如下所示：

使用斯特吉斯规则确定直方图中使用的框数

请注意，这似乎足以很好地了解值的基本分布，而不会因为数量太多而无法简单地可视化数据中的噪声。

斯特奇斯规则的共同价值观

下表显示了根据斯特吉斯规则，基于数据集中的观测总数的直方图中使用的最佳组数：

不同样本量的斯特吉斯规则

斯特奇斯规则的替代方案

斯特吉斯规则是确定直方图中使用的最佳箱数的最常用方法，但还有多种替代方法，包括：

平方根规则：盒子数量 = ⌈√ n ⌉

大米规则：箱数 = ⌈2 * 3 √ n ⌉

Freedman-Diaconis 规则：框数 = (2*IQR) / 3 √ n其中IQR是四分位数范围。

奖励：斯特吉斯规则计算器

使用此免费在线计算器自动应用斯特吉斯规则，根据数据集的大小确定用于直方图的最佳组数。

posted @ 2025-04-11 16:02  papering  阅读(75)  评论(0)    收藏  举报