Wired Sum

Wired Sum

题目描述
给定以一个 n * m 的矩阵，矩阵每个元素的数值代表颜色，求相同颜色元素的曼哈顿距离

题目链接

---

解题思路

让求所有相同颜色的曼哈顿距离，对于求某一种颜色的距离，可以分成两步，第一步求出相同颜色的，延 x 轴方向上的距离，第二步求延 y 轴方向上的距离，然后相加，其他颜色亦是如此。以求延 x 轴方向上的距离为例（y轴同理），把所有点的横坐标从小到大排序，

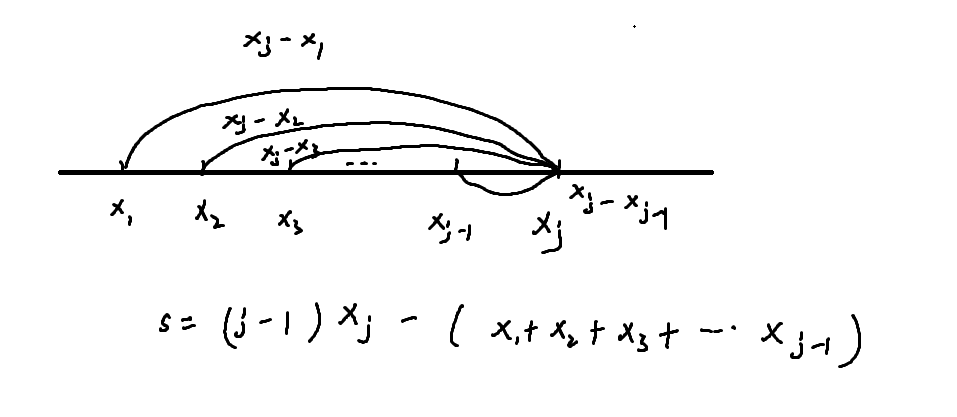
求 \(x_j\) 之前的点到 \(x_j\) 的距离s(若下标从0开始)，则有 s = j * \(x_j\) - (\(x_0\) + \(x_1\) + ... + \(x_j-1\))，后者刚好是前 j-1 项的和，其次就是存颜色，在这里用vector存储，因为只知道 n * m的范围，所以不能直接开辟数组空间，vector初始开辟空间为 0。

代码

#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#define int long long
#define endl '\n'
 
using namespace std;
 
const int N = 1e5 + 10;
 
typedef pair<int, int> PII;
 
vector<int> x[N], y[N];  //x[i][j] 表示第 j 个颜色为 i 的点出现的行号，同理 y 表示列号
int t, n, m;
 
void solve() {
    int ans = 0;
    cin >> n >> m;
    vector<vector<int>> g(n + 1, vector<int> (m + 1));  //用来存储颜色
 
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= m; j++){
            cin >> g[i][j];
            x[g[i][j]].push_back(i);
            y[g[i][j]].push_back(j);
        }
    
    for(int i = 1; i <= 1e5; i++) {
        sort(x[i].begin(), x[i].end());
        int sum = 0; // sum 记录前缀和
        for(int j = 0; j < x[i].size(); j++) {
            ans += j * x[i][j] - sum;
            sum += x[i][j];
        }
 
        sort(y[i].begin(), y[i].end());
        sum = 0;
        for(int j = 0; j < y[i].size(); j++) {
            ans += j * y[i][j] - sum;
            sum += y[i][j];
        }
    }
 
    cout << ans << endl;
}
 
signed main() {r
    solve();
    return 0;
}