洛谷 P1621-集合

集合

---

题目描述

Caima 给你了所有 [a,b] 范围内的整数。一开始每个整数都属于各自的集合。每次你需要选择两个属于不同集合的整数，如果这两个整数拥有大于等于 p 的公共质因数，那么把它们所在的集合合并。
重复如上操作，直到没有可以合并的集合为止。
现在 Caima 想知道，最后有多少个集合。
(保证 1 <= a <= b <= 1e5, 2 <= p <= b)
原题链接

---

Input

10 20 3
1 100 2
10 100 5

Output

7
12
31

解题思路

我们可以先假想一下按这道题的要求进行操作，得到最终结果的过程。它一定是由小于等于 b 的质因数将[a,b],之间的数分成了若干堆，如果两个堆中有相同的节点，则在对这两个堆进行合并，进而得到最终结果。所以，我们的目的就明确了

• 1 . 用质因数初次筛选
• 2 . 根据公共元素和并堆
  举个栗子吧：
  区间[2,12],p = 2,用2筛选得到 2，4，6，8，10，12，用3筛选得到 3，6，9，12，用5筛选得到 5，10，用7筛选得到 7，用 11筛选得到 11，初步筛选到此结束。用肉眼观察的话，很容易就能看出，前三堆是可以合并到一起的，合并完之后5堆就变成了3堆，答案是3。怎么合并呢？用并查集啊，我们让每一个堆的祖宗都等于这个堆的第一个数
  
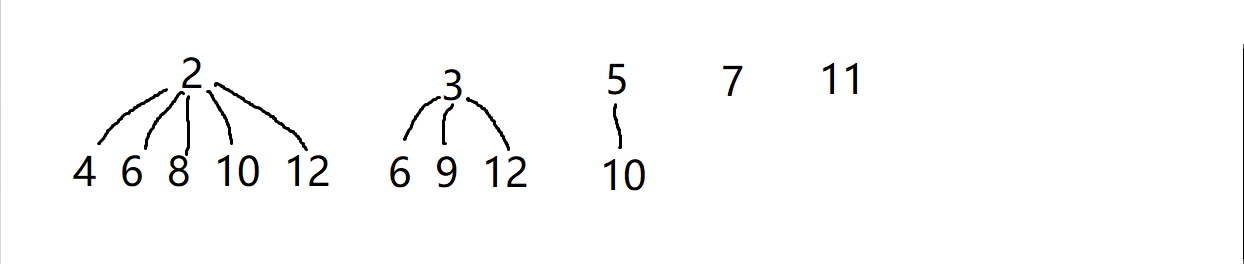
  得到这样的结果，在祖宗为2的堆里面，第一次出现了6，我们让6的祖宗为2，但在祖宗为3的堆中也出现了6，6的祖宗该如何变化呢？我们通过6可以直接的到它的祖宗节点2，我们再次遍历到6时，只需要把2指向3就行了，这样惊奇的发现这两个堆就合并了
  
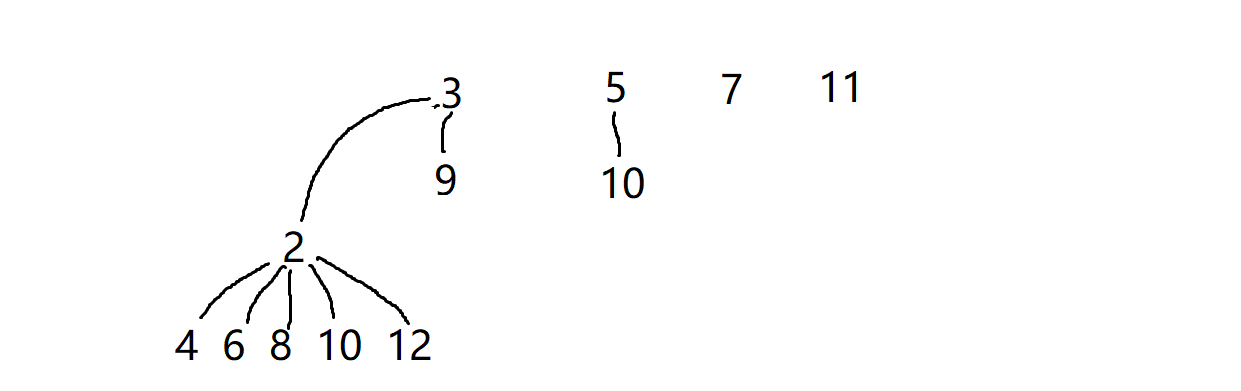
  再总结一下规律可以发现，每合并一次，剩余堆数只会减少一个，所以我们可以先让ans = r-l+1,每合并一次就 ans--，最后直接输出ans即可。

AC代码

#include <iostream>
using namespace std;
const int N = 1e5 + 10;
int p[N],l,r,q,ans; // p存节点之间的关系p[i] = j，表示 i 的祖宗是 j
bool st[N]; // 埃氏筛法，st标记被筛选过的数
void init (){
    for(int i = l; i <= r; i++) //初始化，先让每个节点的祖宗等于自己
        p[i] = i;
}
int find (int x){
    if(p[x] != x) p[x] = find(p[x]);
    return p[x];
}
void getPrime(){ //进行筛选与合并
    for(int i = 2; i <= r; i++){ // i 为当前筛选使用的素数
        if(!st[i]){
            if(i >= q){ // 保证素数大于 p
                for(int j = i + i; j <= r; j += i){
                    st[j] = true;
                    if(j-i >= l && find(j) != find(j-i))
                        p[find(j)] = find(j-i),ans--; // 如果j的祖宗与它前一个的不同，就让j的祖宗指向j-i的祖宗
                }
            }
            else
                for(int j = i + i; j <= r; j += i)
                    st[j] = true;
        }
    }
}
int main(){
    scanf("%d %d %d",&l,&r,&q);
    init();
    ans = r - l + 1;
    getPrime();
    printf("%d",ans);
    return 0;
}