浅谈动态 dp

DDP，即动态动态规划，一般是指在原有的 DP 模型上不断对初始值进行修改并得出答案。

一般而言都是进行单点修改，并且搭配数据结构以及矩阵进行实现。

这里要先给出一个前置知识：

广义矩阵乘法

原矩阵乘法式子为 \(C_{i,j}=\sum_kA_{i,k}\times B_{k,j}\)。

其实写成这样同样是满足矩阵乘法的性质的：\(C_{i,j}=\max_k(A_{i,k}+B_{k,j})\)。

事实上只要广义上的 \(+\) 满足交换律，\(\times\) 满足交换律与结合律，且 \(\times\) 对 \(+\) 存在分配律时矩阵乘法都是有结合律和分配律的性质的。

接下来进入正题：

动态DP

先看一道例题：

GSS 3 - Can you answer these queries III

给定一个长度为 \(n\) 的序列 \(A\) ，以及 \(m\) 次操作，操作有两种类型:

• 1,x,y：将 \(A_x\) 修改为 \(y\) 。
• 2,l,r：求 \(\max\{A[i]+A[i+1]+···+A[j]\}\ (l \le i \le j\le r)\)。

---

其实就是单点修改最大子段和。

显然可以线段树为维护前缀最大和与后缀最大和，但是我们今天讨论另一种解法：动态 DP。

先想一想如果没有修改并且是单纯求全局最大子段和是怎么求的。

转移式子显然是 \(dp_i=\max(dp_{i-1}+a_i,a_i)\)。

发现可以用一开头介绍的 \(\max+\) 矩阵来完成这个转移式：

\[\begin{bmatrix}dp_{i-1}\\0\end{bmatrix}\times\begin{bmatrix}a_i & -\infty \\a_i & 0\end{bmatrix}=\begin{bmatrix}dp_{i}\\0\end{bmatrix} \]

因此可以使用线段树来维护从而支持区间操作，单点修改同样迎刃而解了。

luogu P4751 【模板】动态 DP（加强版）

给定一个 \(n\) 个点的带点权树，进行 \(m\) 次修改点权的操作。

你需要在每次修改之后输出树上最大带权独立集的权值之和。

\(1\le n \le 10^6,1\le m\le 3\times10^6\)。

---

老样子，先出来 DP 式子：

\[dp_{u,0}=\sum_{v\in son_u} \max(dp_{x,0},dp_{x,1}),dp_{u,1}=\sum_{v\in son_u} dp_{x,0} \]

非常好想。

这同样可以使用矩阵进行维护，吗？

由于操作都是在树上进行，一个点有可能从多个儿子节点合并，有没有办法只从一个节点合并并且能保证复杂度的做法呢？

有的，兄弟，有的：重链剖分。

令 \(g_{u,0/1}\) 表示只考虑 \(u\) 的轻儿子的选/不选 \(u\) 的最大权独立集，\(dp_{u,0/1}\) 表示轻重儿子都考虑。

最后的答案就是 \(\max(dp_{1,0},dp_{1,1})\)。

由于每个点到根节点所经过的轻边不超过 \(\log n\) 条，所以可以直接暴力 DP 转移所有的 \(g_{u,0/1}\)。

令 \(son_u\) 表示 \(u\) 的重儿子，则矩阵如下：

\[\begin{bmatrix}dp_{son_u,0}&dp_{son_u,1}\\-\infty&-\infty\end{bmatrix}\times\begin{bmatrix}g_{u,0}&g_{u,1}\\g_{u,0}&-\infty\end{bmatrix}=\begin{bmatrix}dp_{u,0}&dp_{u,1}\\-\infty&-\infty\end{bmatrix} \]

（两个都开 \(2\times 2\) 只是个人习惯）

直接用树剖维护就行了，细节有点多，看代码吧：

PS：这是经过了加强版毒打后的卡常代码。

#include <bits/stdc++.h>
using namespace std;
const int N = 1000010;
vector<int> h[N];
int n, m, num_cnt;
int a[N];
int seg[N], rev[N], son[N], siz[N];
int fa[N], dep[N], top[N], low[N];
int g[N][2];
int rt[N], idx;
inline int read() {
	int x = 0, f = 1;
	char c = getchar();
	while (c < '0' || c > '9') {
		if (c == '-') f = -1;
		c = getchar();
	}
	while (c >= '0' && c <= '9') {
		x = x * 10 + c - '0';
		c = getchar();
	}
	return x * f;
}
struct mat {
	int a[2][2];
	mat() { memset(a, 0, sizeof a); }
	friend mat operator * (mat x, mat y) {
		mat z;
		for (int i = 0; i < 2; i ++ ) for (int j = 0; j < 2; j ++ ) {
			z.a[0][0] = max(x.a[0][0] + y.a[0][0], x.a[0][1] + y.a[1][0]);
			z.a[0][1] = max(x.a[0][0] + y.a[0][1], x.a[0][1] + y.a[1][1]);
			z.a[1][0] = max(x.a[1][0] + y.a[0][0], x.a[1][1] + y.a[1][0]);
			z.a[1][1] = max(x.a[1][0] + y.a[0][1], x.a[1][1] + y.a[1][1]);
		}
		return z;
	}
}hh;
static void dfs1(int u, int father) {
	fa[u] = father;
	dep[u] = dep[fa[u]] + 1;
	siz[u] = 1;
	for (int x : h[u]) if (x != fa[u]) {
		dfs1(x, u);
		siz[u] += siz[x];
		if (siz[x] > siz[son[u]]) son[u] = x;
	}
}
static void dfs2(int u) {
	if (son[u]) {
		top[son[u]] = top[u];
		seg[son[u]] = ++ num_cnt;
		rev[num_cnt] = son[u];
		dfs2(son[u]);
	}
	for (int x : h[u]) if (!top[x]) {
		top[x] = x;
		seg[x] = ++num_cnt;
		rev[num_cnt] = x;
		dfs2(x);
	}
}
struct TREE {
	int l, r;
	mat s;
}tr[N * 4];
inline static void pushup(int k) { tr[k].s = tr[tr[k].r].s * tr[tr[k].l].s; }
static void change(int &k, int l, int r, int p) {
	if (!k) k = ++idx;
	if (l == r) {
		mat &it = tr[k].s;
		it.a[0][0] = it.a[1][0] = g[rev[p]][0];
		it.a[0][1] = g[rev[p]][1];
		it.a[1][1] = -1e9;
		return ;
	}
	int mid = l + r >> 1;
	if (p <= mid) change(tr[k].l, l, mid, p);
	else change(tr[k].r, mid + 1, r, p);
	pushup(k);
}
static void build_tree(int u) {
	for (int x : h[u]) if (x != fa[u] && x != son[u]) {
		build_tree(x);
		mat it = hh * tr[rt[x]].s;
		g[u][0] += max(it.a[0][0], it.a[0][1]);
		g[u][1] += it.a[0][0];
	}
	if (son[u]) build_tree(son[u]);
	change(rt[top[u]], seg[top[u]], low[top[u]], seg[u]);
}
static void DO(int u) {
	int x = seg[top[u]], y = low[top[u]];
	mat it1 = hh * tr[rt[top[u]]].s;
	change(rt[top[u]], x, y, seg[u]);
	mat it2 = hh * tr[rt[top[u]]].s;
	int f = fa[top[u]];
	if (!f) return;
	g[f][0] -= max(it1.a[0][0], it1.a[0][1]);
	g[f][1] -= it1.a[0][0];
	g[f][0] += max(it2.a[0][0], it2.a[0][1]);
	g[f][1] += it2.a[0][0];
	DO(f);
}
int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);
	n = read(), m = read();
	for (int i = 1; i <= n; i ++ ) a[i] = read(), g[i][1] = a[i];
	for (int i = 1; i < n; i ++ ) {
		int x = read(), y = read();
		h[x].push_back(y);
		h[y].push_back(x);
	}
	dfs1(1, 0);
	top[1] = rev[1] = seg[1] = num_cnt = 1;
	dfs2(1);
	for (int i = 1; i <= n; i ++ ) low[top[i]] = max(low[top[i]], seg[i]);
	build_tree(1);
	int la = 0;
	while (m -- ) {
		int x = read(), y = read();
		x ^= la;
		if (a[x] == y) {
			cout << la << '\n';
			continue;
		}
		g[x][1] -= a[x];
		a[x] = y;
		g[x][1] += y;
		DO(x);
		mat it = hh * tr[rt[1]].s;
		la = max(it.a[0][0], it.a[0][1]);
		cout << la << '\n';
	}
	return 0;
}

「CF573D」Bear and Cavalry

有 \(n\) 个人和 \(n\) 匹马，第 \(i\) 个人对应第 \(i\) 匹马。第 \(i\) 个人能力值 \(w_i\)，第 \(i\) 匹马能力值 \(h_i\)，第 \(i\) 个人骑第 \(j\) 匹马的总能力值为 \(w_i\times h_j\)，整个军队的总能力值为 \(\sum w_i\times h_j\)（一个人只能骑一匹马，一匹马只能被一个人骑）。有一个要求：每个人都不能骑自己对应的马。让你制定骑马方案，使得整个军队的总能力值最大。

现在有 \(q\) 个操作，每次给出 \(a,b\)，交换 \(a\) 和 \(b\) 对应的马。每次操作后你都需要输出最大的总能力值。

\(2 \le n \le 30000,1\le q \le 10000\)。

---

比较有意思的一道题。

想一想如果没有不能骑对应的马该怎么做？

显然是排序一遍直接乘。

现在考虑有需要对应的情况，我们依然从大到小排序后做（这里懒得讲了，直接引用一张网上找到的题解的图）

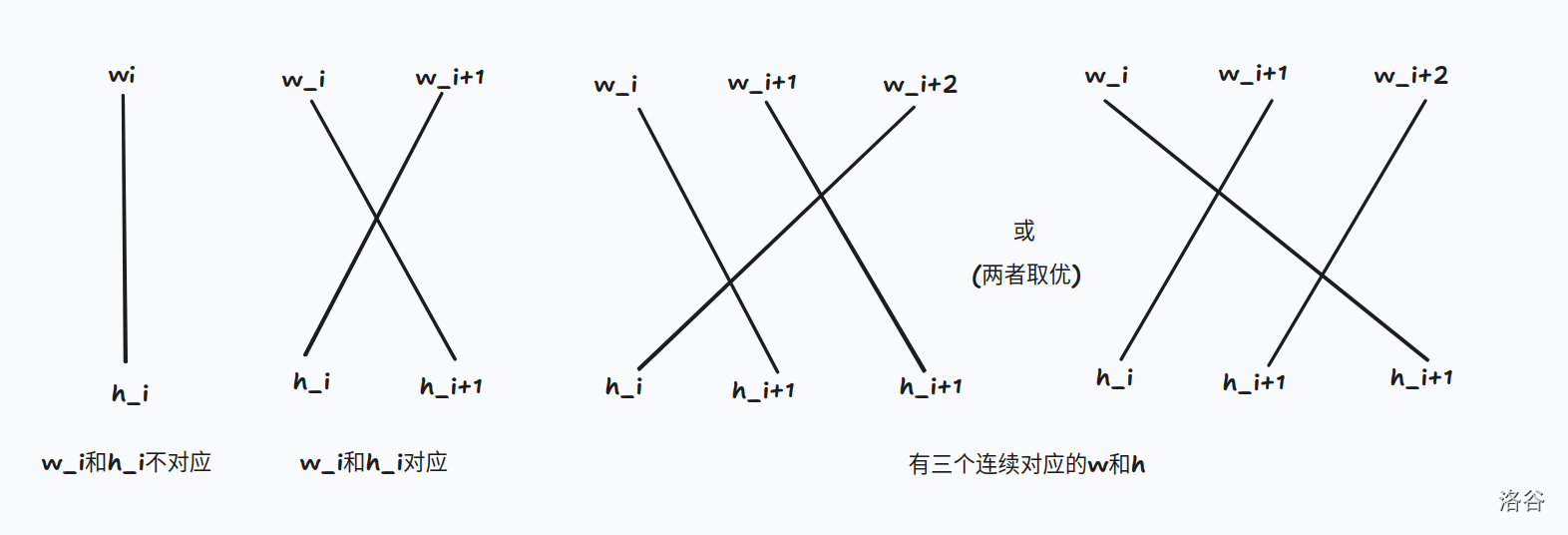
考虑如果有 \(4\) 个连续的，其实直接当作两个两个的就行，依次可以发现每一个 \(\ge 4\) 的都可以拆成 \(2/3\)，并且肯定是最优的。

（事实上这篇题解讲漏了一些，比如理论上应该在 \(2/3\) 中取 \(\max\)，因为可能会存在对应+不对应+对应的情况）

然后直接矩阵中维护 \(dp_i,dp_{i-1},dp_{i-2}\) 就行了，剩下有一点点细节，但是相对就十分简单了。

（吐槽：这玩意数据范围那么小，\(nq\) 暴力都能过）

---

感觉这个东西做多了就完全是套路了，不算难。