wqs 二分

由巨佬王钦石再 2012 年的国家集训队论文里提出，之后逐步传播到全球。

解决的问题基本都形如：给定一个具有凸性质的函数 \(f(x)\)。然后给你一个确定的 \(m\) 要你求 \(f(m)\) 的值。

这里讨论 \(f\) 是上凸的情况，下凸同理。

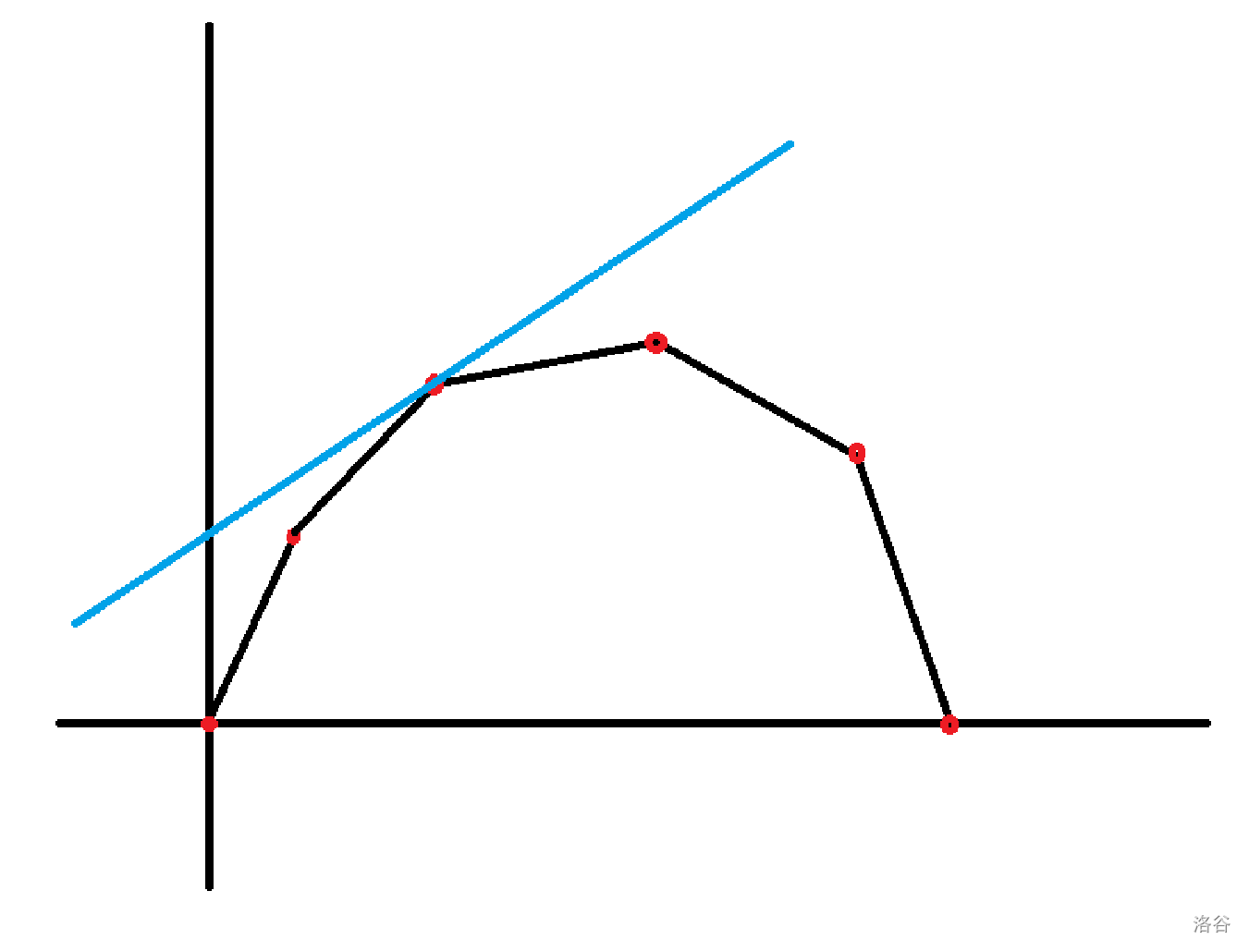
发现当确定了斜率 \(k\) 后截距的最大值就确定了，所以考虑二分斜率，知道交点落在 \(m\)。

若直线的交在 \(x\)，则会有 \(f(x)=kx+b\)，\(b=f(x)-kx\)，要求截距的最大值就只需要将 \(f\) 函数的差分数组总体减去 \(k\) 然后贪心或 dp 就可以了。此时求出的最大值如果 \(<m\) 则说明 \(k\) 大了，否则是小了。

这里还有一个问题，我们二分时为了保证复杂度都是整数二分，此时如果有多个交点要怎么办？

很简单，在二分的 \(check\) 函数中求最大值时当值相同优先选 \(x\) 较小的，二分时求满足条件的最大的 \(k\) 就行了。

最终将截距的最大值加 \(m \times k\) 就是正确答案。

复杂度为一般为 \(\text{O}(n \log V)\)，check 时可能会用到额外的数据结构。

[国家集训队] Tree I

给你一个无向带权连通图，每条边是黑色或白色。让你求一棵最小权的恰好有 \(need\) 条白色边的生成树。

题目保证有解。

\(1 \le N \le 5\times10^4，1 \le M \le 10^5\)。

---

板子题。

令 \(f(x)\) 表示选择 \(x\) 个白色边所能得到的最小生成树。

显然这是一个下凸的函数。直接二分斜率 \(k\)，然后将所有白边的边权减 \(k\)，求最小生成树就行，最终答案加上 \(k \times need\) 就行。

这里有个细节，一开始将白边黑边单独排序，之后合并的时候归并一下就行了，可以省一个 \(\log\)。

#include <bits/stdc++.h>
using namespace std;
const int N = 50010, M = 100010;
int n, m, k, ans;
struct P {
	int x, y, z, c;
	bool operator < (const P &b) const { return z < b.z; }
}s[3][M];
int cnt[3], fa[N];
int get(int x) {
	if (x == fa[x]) return x;
	return fa[x] = get(fa[x]);
}
int check(int mid) {
	int i0 = 1, i1 = 1, num = 0;
	cnt[2] = 0;
	while (i0 <= cnt[0] || i1 <= cnt[1]) {
		if (i0 <= cnt[0] && (i1 > cnt[1] || s[0][i0].z + mid <= s[1][i1].z))
			s[2][++cnt[2]] = s[0][i0 ++], s[2][cnt[2]].z += mid;
		else s[2][++cnt[2]] = s[1][i1 ++];
	}
	for (int i = 1; i <= n; i ++ ) fa[i] = i;
	ans = 0;
	for (int i = 1; i <= cnt[2]; i ++ ) {
		int x = get(s[2][i].x), y = get(s[2][i].y), z = s[2][i].z, c = s[2][i].c;
		if (x != y) {
			fa[x] = y;
			ans += z;
			if (!c) num ++;
		}
	}
	return num;
}
int main() {
	cin >> n >> m >> k;
	for (int i = 1; i <= m; i ++ ) {
		int x, y, z, c;cin >> x >> y >> z >> c;
		x ++, y ++;
		s[c][++cnt[c]] = {x, y, z, c};
	}
	sort(s[0] + 1, s[0] + cnt[0] + 1);
	sort(s[1] + 1, s[1] + cnt[1] + 1);
	int l = -101, r = 101;
	while (l < r) {
		int mid = l + r + 1 >> 1;
		if (check(mid) >= k) l = mid;
		else r = mid - 1;
	}
	cerr << check(l) << '\n';
	cout << ans - k * l;
	return 0;
}

[八省联考 2018] 林克卡特树

给你一棵 \(n\) 个点的无根树，有负边权，你可以删去 \(k\) 条边然后任意加上 \(k\) 条权值为 \(0\) 的边。

求最终的直径的最大值。

\(1 \le n \le 3 \times 10^5\)

---

好题。

转换一下题面：求在原树选出 \(k+1\) 个不相交链的最大总权重（单个点也算一条链）。

怎么做呢？可以 dp。

\(dp_{i,j,0/1/2}\) 表示以 \(i\) 为根的子树中选取了 \(j\) 条链且 \(i\) 的度数为 \(0/1/2\)。

转移很好想，这里就不写了。

这样做是 \(\text{O}(n^2)\)。

打表可以发现令选取 \(x\) 条链的最大总权重为 \(f(x)\)，则 \(f(x)\) 为一个上凸函数。

此时就可以 wqs 二分了。

然后 \(j\) 这一维就被成功删掉了，\(\text{O}(n)\) 树型 dp 就行。当然，写的时候要注意要重载一下小于号，让最终答案的 \(k\) 值尽可能小。

细节有点多。

#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 300010, M = N * 2;
int e[M], ne[M], h[N], w[M], idx;
int n, m;
void add(int a, int b, int c) { e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++; }
struct P {
	int val, k;
	bool operator < (const P &b) const {
		if (val != b.val) return val < b.val;
		return k > b.k;
	}
	friend P operator + (P a, P b) { return {a.val + b.val, a.k + b.k}; }
	friend P operator + (P a, int b) { return {a.val + b, a.k}; }
}dp[N][3];
P tmp;
void dfs(int u, int fa, int mid) {
	for (int i = h[u]; i != -1; i = ne[i]) {
		int x = e[i];
		if (x == fa) continue;
		dfs(x, u, mid);
		dp[u][2] = max(dp[u][2] + dp[x][0], dp[u][1] + dp[x][1] + w[i] + tmp);
		dp[u][1] = max(dp[u][1] + dp[x][0], dp[u][0] + dp[x][1] + w[i]);
		dp[u][0] = dp[u][0] + dp[x][0];
	}
	dp[u][0] = max(dp[u][0], max(dp[u][1] + tmp, dp[u][2]));
}
int check(int mid) {
	tmp = {mid, 1}; 
	for (int i = 1; i <= n; i ++ ) {
		dp[i][0] = {0, 0};
		dp[i][1] = {0, 0};
		dp[i][2] = {mid, 1};
	}
	dfs(1, 0, mid);
	return dp[1][0].k;
}
signed main() {
	ios::sync_with_stdio(0);
	cin.tie(0); 
	memset(h, -1, sizeof h);
	cin >> n >> m;m ++;
	for (int i = 1; i < n; i ++ ) {
		int x, y, z;cin >> x >> y >> z;
		add(x, y, z);
		add(y, x, z);
	}
	int l = -1e13, r = 1e13;
	while (l < r) {
		int mid = l + r + 1 >> 1;
		if (check(mid) <= m) l = mid;
		else r = mid - 1;
	}
	cerr << l << ' ' << check(l) << '\n';
	cout << dp[1][0].val - l * m;
	return 0;
}