从反悔贪心到模拟费用流

反悔贪心

又名可撤销贪心，我的理解是通过对权值做一些等价转换使得在进行贪心的过程中可以同时进行撤销操作。

简单地不全面地举个例子：在开始贪心的选择了 \(w_i\)，然后最优的方案其实是选择 \(w_j\)，此时将 \(j\) 的价值改为 \(w_j-w_i\)，由于没到达最优解前会一直进行下去，所以一定会选到 \(j\)，\(w_i\) 就被替换为了 \(w_j\)。

事实上反悔贪心的题的权值构造都十分巧妙，要结合题目具体分析。

[CF865D]Buy Low Sell High

给定某只股票接下来 \(N\) 天的价格，你每天要么什么都不干，要么买入一股，要么卖出一股。

求在第 \(N\) 天结束时的最大盈利。

板子题。

为了方便所有不卖的日子全都买股票，贡献再买股票的一天统一计算。

贪心的想，若要卖出一张股票则选取可能的最小的买入价格。

但有可能当前遍历到的第 \(i\) 天并不是卖出第 \(j\) 张股票的最佳时间，但此时我们却仍然会将答案加上 \(w_i-w_j\)，此时为了支持撤销可以同时在第 \(i\) 天买一张股票。往后如果在第 \(k\) 天是卖出第 \(j\) 天买入的股票的最好时机，那么 \(k\) 就对应上了 \(i\)，权值就会变为 \(w_k-w_i+w_i-w_j=w_k-w_j\)，等价。

直接看代码吧，清楚得多。

#include <bits/stdc++.h>
using namespace std;
#define int long long
signed main() {
	priority_queue<int, vector<int>, greater<int> > q;
	int n;cin >> n;
	int ans = 0;
	for (int i = 1; i <= n; i ++ ) {
		int x;cin >> x;
		q.push(x);
		if (q.top() < x) {
			ans += x - q.top();
			q.pop();q.push(x);
		}
	}
	cout << ans;
	return 0;
}

[2022 集训队互测]Astral Birth

给定一个长度为 \(N(1\le N \le 5\times10^5)\) 的 \(01\) 序列。对于每个 \(k \in [1,n]\)，求出将原序列分任意为 \(k\) 段后重新排列所能得到的 最长不降子序列。

非常好的一道题目。

这里有一个非常巧妙的转换：

在原问题中序列上分出来的 \(k\) 段只会有一段的贡献可以是这一段的最长不降子序列，即 \(01\) 交界处的那一段。剩余的要么是只有 \(0\) 产生贡献，要么是只有 \(1\)。这时候发现，最长不降子序列作为贡献的那一段同样可以拆成一段 \(0\) 贡献和一段 \(1\) 贡献。

所以原问题就可以变成把序列拆成 \(k+1\) 段，每一段中取 \(0/1\) 的个数作为贡献的最大总贡献。

显然连续的 \(01\) 段是一定会绑在一块的，所以就可以缩在一起。

此时原序列就由 \(01\) 交替的块组成。

再次转化，每一块只有 \(0,1\) 中的一个才能产生贡献，等价于删掉另一些。

题目就可以变为删掉一些段，求把剩下的相邻的同颜色段缩在一起后剩下 \(k\) 段的最大长度。

很显然将相邻的块同时删去一定不会更优，毕竟只删一个另一个就一定可以缩掉。

由于不会删掉相邻的块，没删一个块就一定会减少两个块（缩相同颜色块后），边界只能减少一个，不过只需要最开始 \(2 \times 2\) 枚举一下边界的情况就行了。

反悔贪心。

先将所有点都放入小根堆中，每次弹出的点就代表要删除。

由于序列中有删除块的操作，很容易想到使用链表来维护。

假如当前删掉了 \(u\) 点，\(pr_u\) 和 \(ne_u\) 就合并到了一起，为了方便，我们把它作为新的 \(u\)，然后将 \(pr_u\) 和 \(ne_u\) 删去。

过后还有可能继续删去 \(u\) 点，此时一开始被删去的 \(u\) 点的权值就会被重新用到，而 \(pr_u\) 和 \(ne_u\) 就没了。

考虑设计一个新的权值满足撤销的操作。

每次让 \(w_u=w_{pr_u}+w_{ne_u}-w_u\)。容易发现这样每次直接减去 \(w_u\) 就是满足条件的了。

举个例子：最初 \(-w_u\)，后来 \(-(w_{u-1}+w_{u+1}-w_u)\)，抵消，变为 \(-(w_{u-1}+w_{u+1})\)，删去 \(u\) 的操作就被成功撤销了。

一直操作到被缩到只有 \(2\) 个块就行，再删就不符合减去 \(2\) 个颜色块条件了。因此 \(ans_1\) 需要特殊处理一下。

细节有点多。

#include <bits/stdc++.h>
using namespace std;
const int N = 300010;
char s[N];
int a[N], cnt, ans[N], c[N];
int num[N];
int pr[N], ne[N];
bool st[N]; 
struct P {
	int x, p;
	bool operator < (const P &b) const { return x > b.x; }
};
void DEL(int u) {
	st[u] = 1;
	if (pr[u]) ne[pr[u]] = ne[u];
	if (ne[u]) pr[ne[u]] = pr[u];
} 
signed main() {
	ios::sync_with_stdio(0);
	cin.tie(0);
	int n;cin >> n;
	cin >> s + 1;
	int num = 0;
	for (int i = 1; i <= n; i ++ ) num += (s[i] == '1');
	ans[1] = num;
	for (int i = 1; i <= n; i ++ ) {
		if (s[i] == '1') num --;
		else num ++;
		ans[1] = max(ans[1], num);
	}
	int la = 1;
	for (int i = 1; i <= n; i ++ ) if (i == n || s[i] != s[i + 1]) {
		a[++cnt] = i - la + 1;
		la = i + 1;
	}
	for (int i = cnt - 1; i <= n; i ++ ) ans[i] = n;
	for (int l = 1; l <= 2; l ++ ) for (int r = cnt - 1; r <= cnt; r ++ ) {
		if (l > r) continue;
		priority_queue<P> q;
		int now = 0;
		memset(ne, 0, sizeof ne);
		memset(pr, 0, sizeof pr);
		memset(st, 0, sizeof st);
		for (int i = l + 1; i < r; i ++ ) q.push({a[i], i});
		for (int i = l; i <= r; i ++ ) now += a[i], c[i] = a[i], ne[i] = i + 1, pr[i] = i - 1;
		c[l] = c[r] = 1e9;
		for (int k = r - l + 1; k > 2; k -= 2) {
			ans[k - 1] = max(ans[k - 1], now);
			while (1) {
				int x = q.top().x, p = q.top().p;q.pop();
				if (st[p]) continue;
				now -= c[p];
				c[p] = c[pr[p]] + c[ne[p]] - c[p];
				DEL(pr[p]);DEL(ne[p]);
				ans[k - 1] = max(ans[k - 1], now);
				q.push({c[p], p});
				break;
			}
		}
	}
	for (int i = 1; i <= n; i ++ ) ans[i] = max(ans[i], ans[i - 1]);
	for (int i = 1; i <= n; i ++ ) cout << ans[i] << ' ';
	return 0;
}

模拟费用流

讲完反悔贪心，正式进入正题。

其实本质上模拟费用流是一种思想：用各种算法对于特殊结构的费用流进行优化。

老鼠进洞1

一个老鼠必须进一个洞，一个洞最多进一个老鼠。老鼠只能往左走。最小化老鼠行走的距离之和。

发现这可以使用费用流来完成，源点连向所有老鼠，所有洞连向汇点，所有老鼠连向能够到达的洞，权值为距离。

图大概就变成了这样：

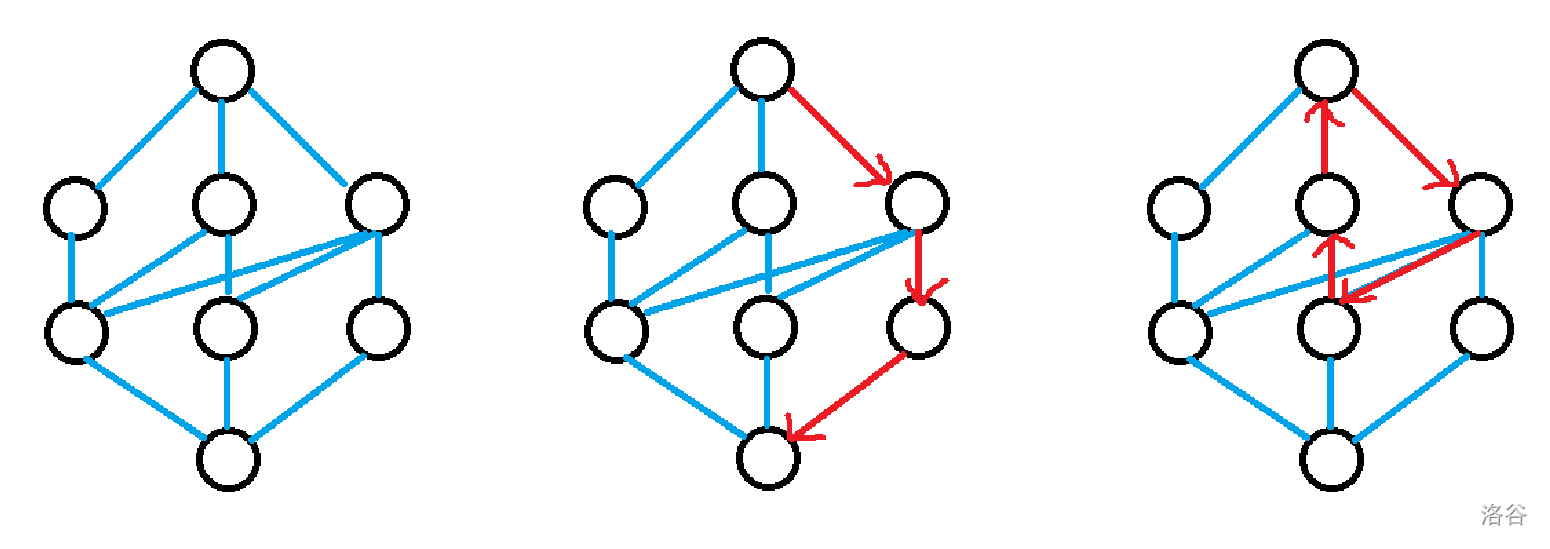
更新费用流就只有上面两种情况：新的增广路或发现负环进行退流。

考虑反悔贪心。

相当于就是从左到右枚举老鼠，每次取最近的一个洞与之匹配，若匹配成功，将这个老鼠也当作一个洞，此时若有后面的老鼠与其匹配，相当于就是图 3 中表示的退流与替换了。

用栈维护就行了。

老鼠进洞2

一个老鼠必须进一个洞，一个洞最多进一个老鼠，洞有附加权值。老鼠只能往左走。最小化老鼠行走的距离与进入的洞的权值之和。

事实上和老鼠进洞1是一样的，只是这里要改成用反悔堆来维护，复杂度多一个 \(\log\)。

老鼠进洞3

一个老鼠必须进一个洞，一个洞最多进一个老鼠。老鼠可以向两边走，洞有附加权值，最小化老鼠行走的距离及选择的洞的权值之和。

这里和老鼠进洞2基本也是一样的，考虑怎么处理往两边走，其实发现只需要同时用洞匹配前面没有选的老鼠就行了，要开两个堆来维护，细节有点多。

老鼠进洞4

一个老鼠必须进一个洞，一个洞最多进一个老鼠，每个位置上可能会有多个老鼠和洞。老鼠可以向两边走，洞有附加权值，最小化老鼠行走的距离及选择的洞的权值之和。

只需要在堆里再维护老鼠或洞的数量，然后批量操作就行了。

其实我说真的，模拟费用流就只是反悔贪心中的一类，只不过解决的题目都可以使用费用流来完成建图，而反悔的内容也可以看作对于费用流内的负环的更新。对我而言说实话感觉硬要把每个模拟费用流的题都和原费用流的图一一对应上反而是显得麻烦了。

[PA 2013] Raper

你需要生产 \(k\) 张光盘。每张光盘都要经过两道工序：先在 A 工厂进行挤压，再送到 B 工厂涂上反光层。

第 \(i\) 天 A 工厂可以花费 \(a_i\) 的费用挤压一张光盘，B 工场可以花费 \(b_i\) 涂一张被挤压过的光盘。

求生产出 \(k\) 张光盘的最小花费。

\(1 \leqslant k \leqslant n \leqslant 5 \times 10^5\)。

发现如果不考虑数据范围这显然可以用费用流做：

当想到模拟费用流时发现有一个总数为 \(k\) 的限制难以处理。

思考一下可以发现由于费用流每次选择最小的一条增广路， \(f(k)\) 就是一个下凸的函数。

考虑使用 wqs 二分。

将每个生产完成的光盘都减去斜率，现在相当于变成了求最大的贡献，和股票买卖比较像。

#include <bits/stdc++.h>
using namespace std;
const int N = 500010;
#define int long long
typedef pair<int, int> PII;
int a[N], b[N];
int n, k, ans;
int check(int mid) {
	ans = 0;
	int num = 0;
	priority_queue<PII, vector<PII>, greater<PII> > q;
	for (int i = 1; i <= n; i ++ ) {
		q.push({a[i] - mid, 1});
		if (q.top().first + b[i] < 0)  {
			ans += q.top().first + b[i];
			num += q.top().second;
			q.pop();
			q.push({-b[i], 0});
		}
	}
	return num;
}
signed main() {
	ios::sync_with_stdio(0);
	cin.tie(0);
	cin >> n >> k;
	for (int i = 1; i <= n; i ++ ) cin >> a[i];
	for (int i = 1; i <= n; i ++ ) cin >> b[i];
	int l = 0, r = 1e18;
	while (l < r) {
		int mid = l + r + 1 >> 1;
		if (check(mid) <= k) l = mid;
		else r = mid - 1;
	}
	check(l);
	cout << ans + l * k;
	return 0;
}

在模拟费用流的题目中当有总流量的额外限制时一般都可以使用 wqs 二分来解决。

当然，只是一般，有的题目还是可以通过一点一点流来实现的。本题要用 wqs 的原因在于题目中有偏序关系的限制导致每次贪心都需要 \(\text{O}(n)\) 便遍历一次。

wqs 二分。

[NOI2019] 序列

给定两个长度为 \(n\) 的正整数序列 \(\{a_i\}\) 与 \(\{b_i\}\)，序列的下标为 \(1, 2, \cdots , n\)。现在你需要分别对两个序列各指定恰好 \(K\) 个下标，要求至少有 \(L\) 个下标在两个序列中都被指定，使得这 \(2K\) 个下标在序列中对应的元素的总和最大。

\(1\le n \le 2\times10^5\)。

一眼盯真可以用费用流，图大概是长这样。

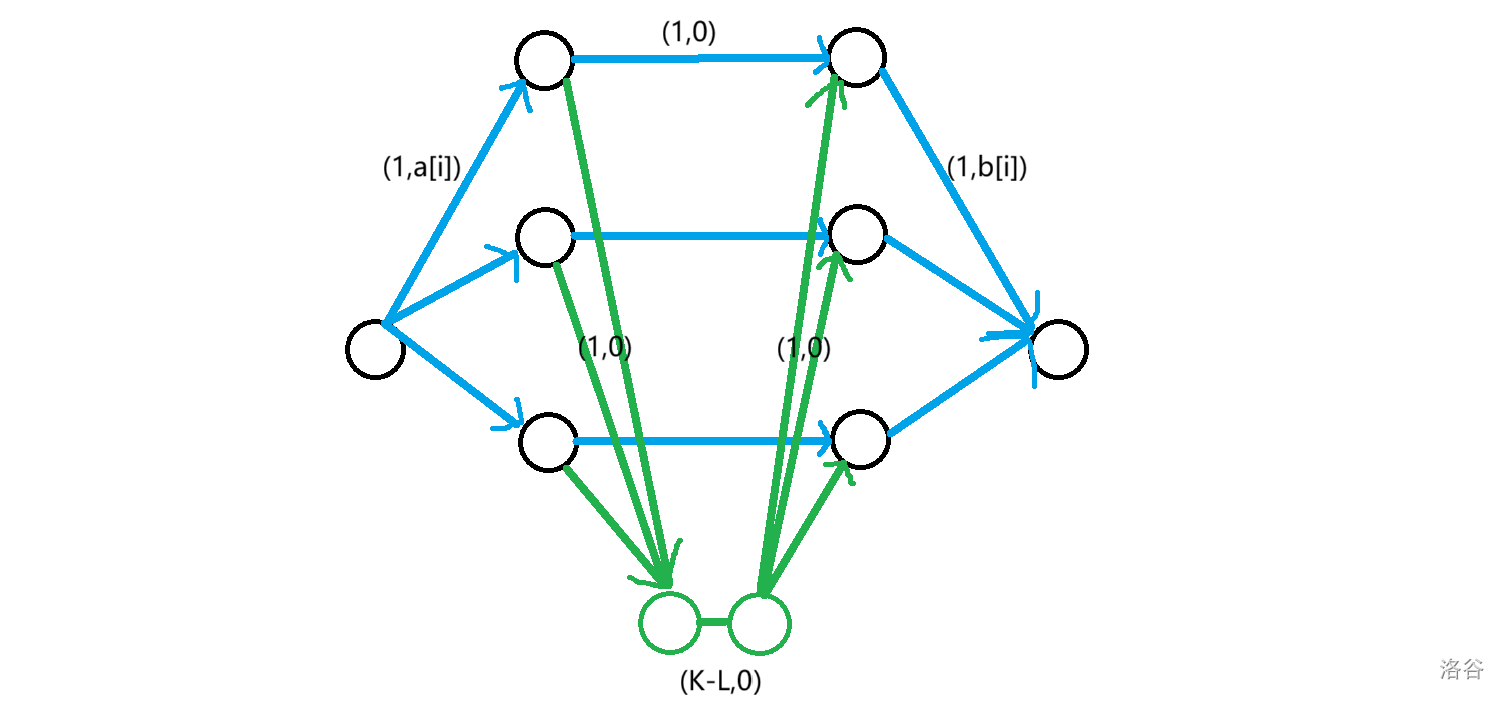
下方两个绿色的点代表下标不同的位置，所以容量为 \(K-L\)。

当然复杂度显然过不了，考虑模拟费用流。

每次照样贪心的选择权值最大的一条增广路，只是这里要注意下方绿色点的容量。

令 \(a_i,b_i\) 都没选过的 \(a_i\) 组成的集合为 \(A\)，只有 \(a_i\) 没选过的为 \(A^{’}\)，\(B\) 与 \(B^{'}\) 同理。

\(a_i,b_i\) 都没选过的直接由 \(a_i,b_i\) 组成一组的构成集合 \(C\)。

发现一共只有 \(5\) 中选择的情况：

\(A,B\)，此时由于两个点都没有选过，绿边的流量要加 \(1\)。
\(A^{'},B\)，另此时两个数分别为 \(i,j\)，\(b_i\) 原先连的 \(k\)，那么此时可以把 \(b_i\) 与 \(k\) 断开，连接 \(a_i,b_i\) 和 \(j,k\)，绿色流量不变。
\(A,B^{'}\)，同上。
\(A^{'},B^{'}\) 差不多的思想，此时绿色流量会减 \(1\)。
\(C\)，此时绿色流量不变。

这样做的话维护 \(5\) 个可删堆就行了。

唉！你说这里也有 恰好 \(K\) 对 的字眼，为什么不用 wqs 二分啊？

当然是因为这道题可以直接在全局状态一条一条增广，而上一题只能一边加点一边增广，并不能在确保在有 \(K\) 对时保证正确性。

吐槽时间：学了半天才感觉模拟费用流这个名字有点误导人，你可以以费用流模型作为切入点，但是如果你要在反悔贪心的每一步都对应上费用流的话就是纯折磨自己，而且也没啥用。

posted @ 2025-03-06 22:13 paper_zym 阅读(113) 评论(0) 收藏举报

刷新页面返回顶部

paper-book

纸书