题解 SP1724 【TRICOUNT - Counting Triangles】

这道题很明显让我们数有多少个三角形,首先我们要观察有什么规律。

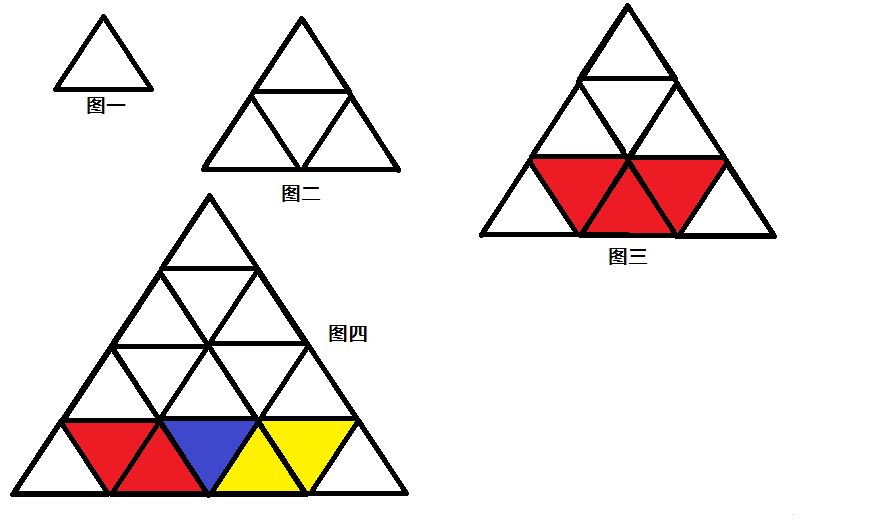
图一只有一个三角形，我们把它看成\(1^2\)，算式：\(1^2=1\)。

图二共有五个三角形，其中有四个是\(2^2\)，再加上（图一），算式：\(1^2+2^2=5\)。

图三共有十三个三角形，其中有九个小三角是\(3^2\)，加上（图二），再减去一个不完整的倒三角，正好是十三个。算式：\(1^2+2^2+(3^2-1)=13\)。

图四共有二十七个三角形。其中有十六个三角形是\(4^2\)，加上（图三），再减去两个倒三角。算式：\(1^2+2^2+(3^2-1)+(4^2-2)=27\)。

图五不详解，算式：\(1^2+2^2+(3^2-1)+(4^2-2)+(5^2-4)=48\)。

图六不详解。算式：\(1^2+2^2+(3^2-1)+(4^2-2)+(5^2-4)+(6^2-6)=78\)。

由此我们可以找出规律正三角个数就是平方和，而倒三角分两种：

当层数为奇数时：倒三角个数\(=n(n+1)(4n-1)/6\)（层数为\(n\)）。

偶数时：倒三角个数\(=n(n+1)(4n+5n)/6\)（层数为\(n\)）。

然后再构思一下代码这题就轻松解决了！

E = mc^2