2498. 青蛙过河 ll

题目链接：

本地要求最大值的最小值，乍一看想的是二分，但仔细想发现是一个思维题。

通过手模可以发现，间隔跳一定是最优的。

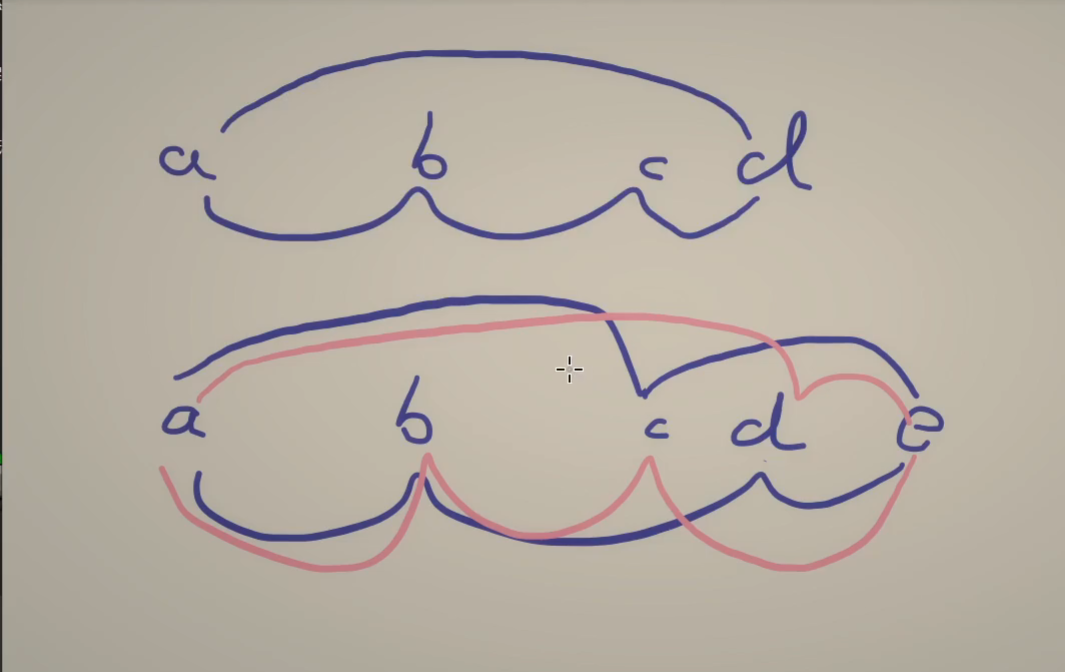
如图所示，\(a \rightarrow d > a \rightarrow c,b \rightarrow d\)。
我们每次都去找间隔为 \(2\) 的元素并求出其差，然后枚举最大值即可。

class Solution {
public:
    int maxJump(vector<int>& stones) {
        int ans = stones[1] - stones[0];//数组长度可能仅为2
        for (int i = 2; i < stones.size(); i++) {
            ans = max(ans, stones[i] - stones[i-2]);
        }
        return ans;
    }
};

详细证明如下：

先将问题转化。将题目中这只青蛙的回程（即从最后一块石头返回第一块石头的路径）反向，看成是第二只青蛙从第一块石头跳到最后一块石头。这样问题就变成：

有两只青蛙一开始都在第一块石头，它们都需要到达最后一块石头，同时每块石头至多到到达一次，求这两只青蛙的最大跳跃长度。

接下来采用 贪心策略，让这两只青蛙从第一块石头跳到最后一块石头。假设有 n 块石头，考虑一般性，我们不妨假设 n >= 3，接下来我们不妨先按 n 的奇偶性分别来模拟一下（画图模拟可能会更清晰🤣）：

首先，我们不妨让第一只青蛙先跳，第二只青蛙后跳，两只青蛙交替着跳。

当 n 为奇数时，不妨设 n = 5，[0 1 2 3 4]：

第一只青蛙第 1 步：0 -> 1

第二只青蛙第 1 步：0 -> 2

第一只青蛙第 2 步：1 -> 3

第二只青蛙第 2 步：2 -> 4，第二只青蛙到达最后一块石头，停止。

第一只青蛙第 3 步：3 -> 4，第一只青蛙到达最后一块石头，停止。

最后，

第一只青蛙跳过的路径为：0 -> 1 -> 3 -> 4

第二只青蛙跳过的路径为：0 -> 2 -> 4

然后我们求两只青蛙的最大跳跃长度。观察两只青蛙跳过的路径，不难发现，第二只青蛙的第一跳 0 -> 2 跨越了第一只青蛙的第一跳 0 -> 1，第二只青蛙的最后一跳 2 -> 4 跨越了第一只青蛙的最后一跳 3 -> 4，所以第一只青蛙的第一跳 1 -> 2 和最后一跳 3 -> 4 不可能是最大跳跃。也就是说我们只需要求 0 -> 2，1 -> 3, 2 -> 4 这三跳的的最大长度即可，即：

ans = max(stones[2] - stones[0], stones[3] - stones[1], stones[4] - stones[2])

写成代码就是：

ans = 0
for i in range(2, n):
    ans = max(ans, stones[i] - stones[i - 2])

当 n 为偶数时，不妨设 n = 6，[0 1 2 3 4 5]：

第一只青蛙第 1 步：0 -> 1

第二只青蛙第 1 步：0 -> 2

第一只青蛙第 2 步：1 -> 3

第二只青蛙第 2 步：2 -> 4

第一只青蛙第 3 步：3 -> 5，第一只青蛙到达最后一块石头，停止。

第二只青蛙第 3 步：4 -> 5，第二只青蛙到达最后一块石头，停止。

最后，

第一只青蛙跳过的路径为：0 -> 1 -> 3 -> 5

第二只青蛙跳过的路径为：0 -> 2 -> 4 -> 5

然后我们求两只青蛙的最大跳跃长度。观察两只青蛙跳过的路径，不难发现，第二只青蛙的第一跳 0 -> 2 跨越了第一只青蛙的第一跳 0 -> 1，第一只青蛙的最后一跳 3 -> 5 跨越了第二只青蛙的最后一跳 4 -> 5，所以第一只青蛙的第一跳 1 -> 2 和第二只青蛙的最后一跳 4 -> 5 不可能是最大跳跃。也就是说我们只需要求 0 -> 2，1 -> 3, 2 -> 4, 3 -> 5 这四跳的的最大长度即可，即：

ans = max(stones[2] - stones[0], stones[3] - stones[1], stones[4] - stones[2], stones[5] - stones[3])

写成代码就是：

ans = 0
for i in range(2, n):
    ans = max(ans, stones[i] - stones[i - 2])

综上所述，当 n >= 3 时，求最大跳跃长度的代码有：

ans = 0
for i in range(2, n):
    ans = max(ans, stones[i] - stones[i - 2])

最后，当 n == 2 时，两只青蛙只需一跳就能从第一块石头跳到最后一块石头，最大跳跃长度就是 stones[1] - stones[0]~

于是，我们有求最大跳跃长度的完整代码如下：

class Solution:
    def maxJump(self, stones: List[int]) -> int:
        n = len(stones)

        if n == 2:
            return stones[1] - stones[0]

        ans = 0
        for i in range(2, n):
            ans = max(ans, stones[i] - stones[i - 2])

        return ans
        

最后，我们将 ans 初始化为 stones[1] - stones[0]，就不需要将 n == 2 的情况单独拿出来了~

class Solution:
    def maxJump(self, stones: List[int]) -> int:
        n = len(stones)

        ans = stones[1] - stones[0]
        for i in range(2, n):
            ans = max(ans, stones[i] - stones[i - 2])

        return ans