1039. 多边形三角剖分的最低得分

题目链接：

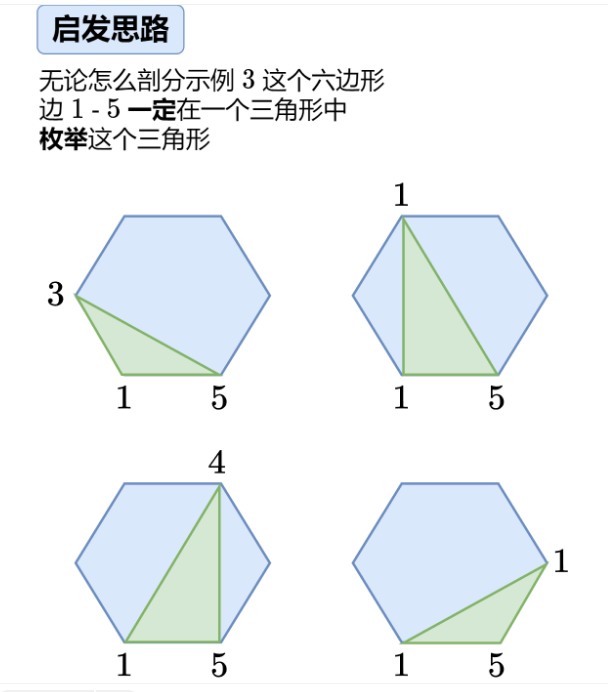
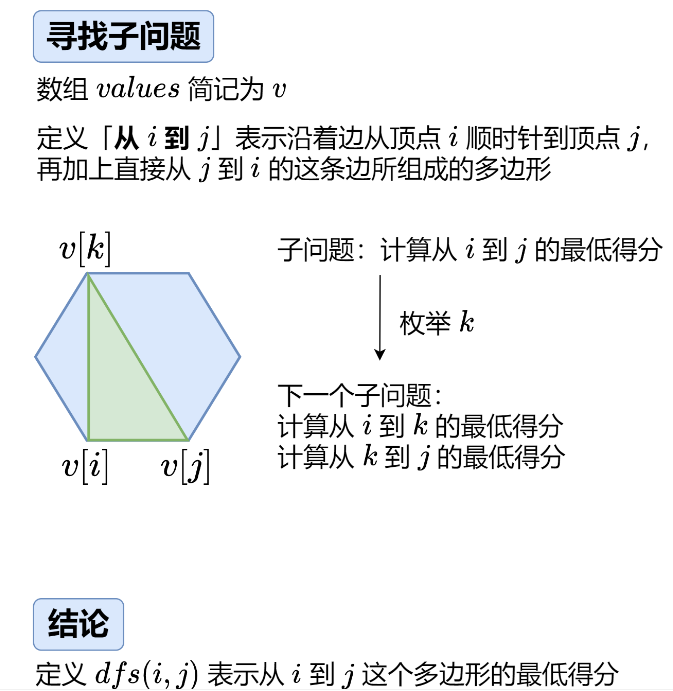
实现一、记忆化搜索

class Solution {
public:
    int minScoreTriangulation(vector<int>& values) {
        int n = values.size();
        int memo[n][n];
        memset(memo, -1, sizeof memo);// -1 表示还没有计算过
        function<int(int, int)> dfs = [&] (int i, int j) -> int {
            if (j == i + 1) return 0;// 只有两个点，无法组成三角形
            int &res = memo[i][j];// 注意这里是引用，下面会直接修改 memo[i][j]
            if (res != -1) return res;
            res = 0x3f3f3f3f;
            for (int k = i + 1; k < j; k++) {
                res = min(res, dfs(i, k) + dfs(k, j) + values[i] * values[k] * values[j]);
            }
            return res;
        };
        return dfs(0, n - 1);
    }
};

实现二、递推

由于 \(i < k\), \(f[i]\) 要从 \(f[k]\) 转移过来必须先计算出 \(f[k]\)，因此 \(i\) 需要倒序枚举；
由于 \(j>k\)，\(f[i][j]\) 要从 \(f[i][k]\) 转移过来必须先计算出 \(f[i][k]\)，所以 \(j\) 需要正序枚举。

此外，因为 \(j\) 至少比 \(i\) 大 \(2\)，即 \(j\) 从 \(i+2\) 开始枚举，为了确保 \(j\) 不越界，则 \(i\) 应该从 \(n-3\) 开始倒序枚举。

class Solution {
public:
    static const int N = 55;
    int f[N][N];
    int minScoreTriangulation(vector<int>& values) {
        int n = values.size();
        memset(f, 0, sizeof f);
        for (int i = n - 3; i >= 0; i--) {
            for (int j = i + 2; j < n; j++) {
                f[i][j] = 0x3f3f3f3f;//确定i和j的取值后即将f[i][j]初始化为正无穷，依靠k来转移状态。
                for (int k = i + 1; k <= j - 1; k++) {
                    f[i][j] = min(f[i][j], f[i][k] + f[k][j] + values[i]*values[k]*values[j]);  
                }
            }
        }
        return f[0][n - 1];
    }
};

参考资料：区间 DP：最长回文子序列