P2181 对角线

题目链接：

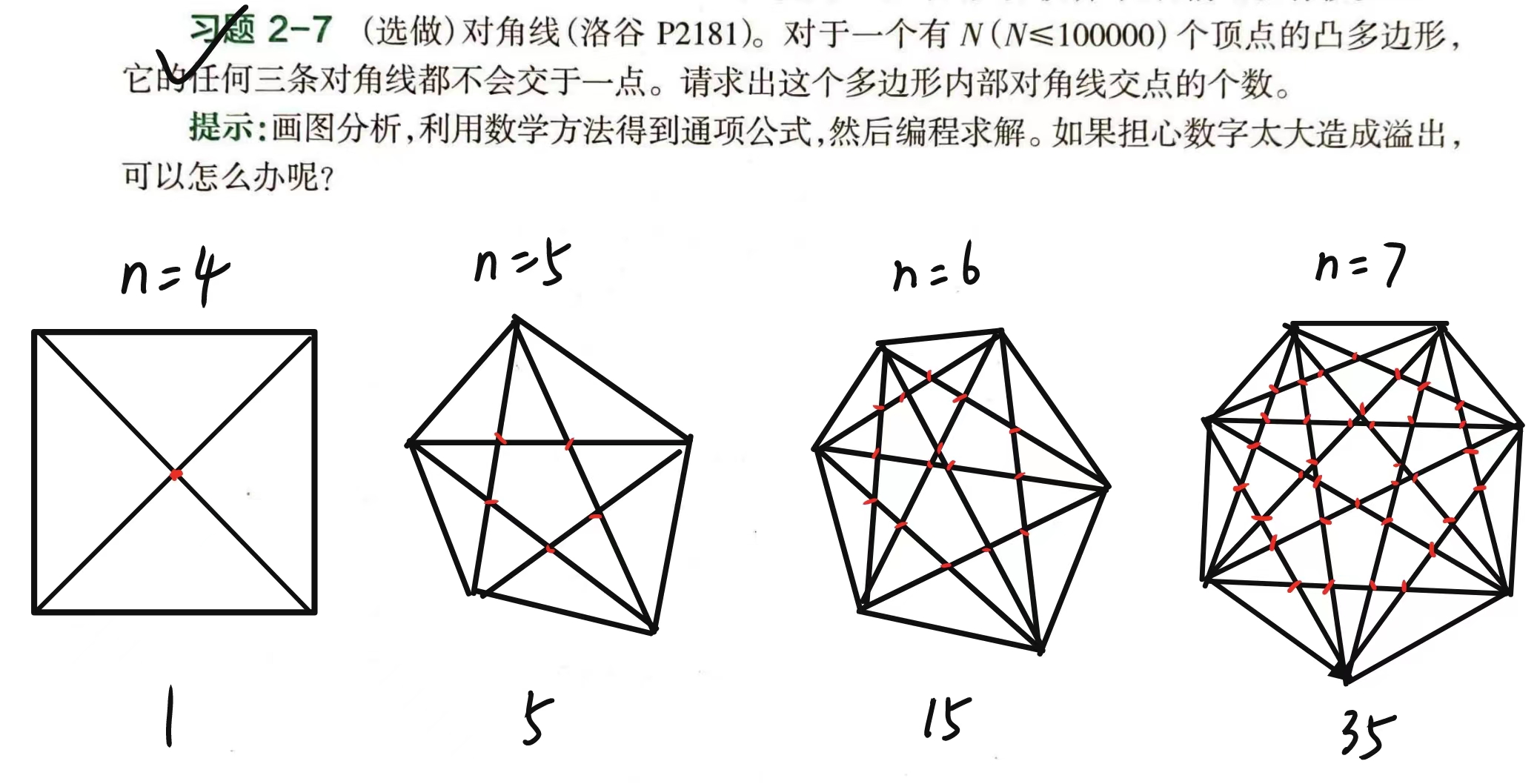
首先由于不会有三条对角线交于一点，所以过某一个交点有且只能有 \(2\) 条对角线。而这两条对角线实质上是确定了 \(4\) 个顶点，因此我们只需要确定 \(4\) 个顶点就得到了这个唯一确定的交点。因此我们只需要求这样４个顶点的搭配有多少个了，也就是从 \(n\) 个顶点中取 \(4\) 个出来，即 \(C\binom{4}{n}\)。
\(n\) 最大取 \(10^5\)，估计范围最大还要比\(\rm long\) \(\rm long\)多出几位，考虑\(\rm unsigned\) \(\rm long\) \(\rm long.\)

#include <bits/stdc++.h>

using namespace std;

unsigned long long n, ans;

int main()
{
    cin >> n;
    ans = n * (n - 1) / 2 * (n - 2) / 3 * (n - 3) / 4;
    cout << ans;
    return 0;
}