Fork me on GitHub

2022/8/17日测试（内含金字塔,斗地主,网络连接,X-Magic Pair,X-Magic Pair）

前言

写这篇题解的时候我已经准备好退役了，由于本人学艺不精，已无力继续。

正文

LINK：X-Magic Pair

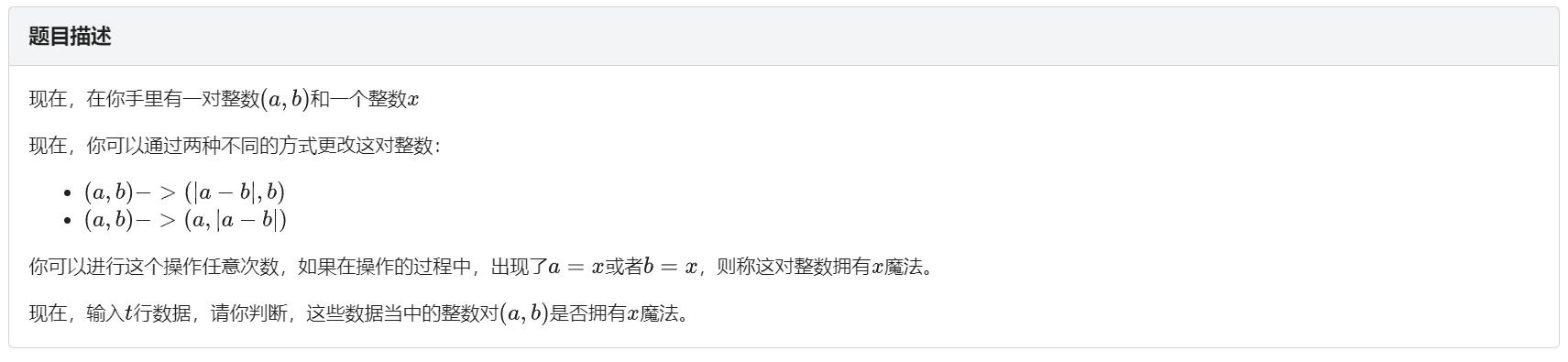
标签：思维，数学，推公式

  在每一步设a>b，则转移是这样的：(a,b) -> ( a - b，b )，(a, a - b) -> 右边：（a, b）, ( b,a-b)

  一个走回去了，一个和左边一样。所以多于每一个，只有（a, b）->(a - b, b) 一种法则。

  那么相当于一直让 a 减去 b，直到 a

 

Code 
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int main() {
	ll t;
	scanf("%lld",&t);
	while(t--) {
		ll flag=0;
		ll x, y, k;
		cin >> x >> y >> k;
    	if (x > y) swap(x, y);
    	while(x) 
    	{
       	 	if (k == x || k == y)  {
       	 		cout << "YES\n";
       	 		flag=1;
       	 		break;
			}
        	y -= x;
        	if (x > y) swap(x, y);
    	}
    	if(!flag)
    	cout << "NO\n";
	}
	return 0;
}

 

最多的个数

标签：RMQ

用一个数组f[i]记录每一个数据出现的次数。再对于f做RMQ。

对于查询的每一区间，可以查这个区间里的最大值。可是这样显然是不对的。

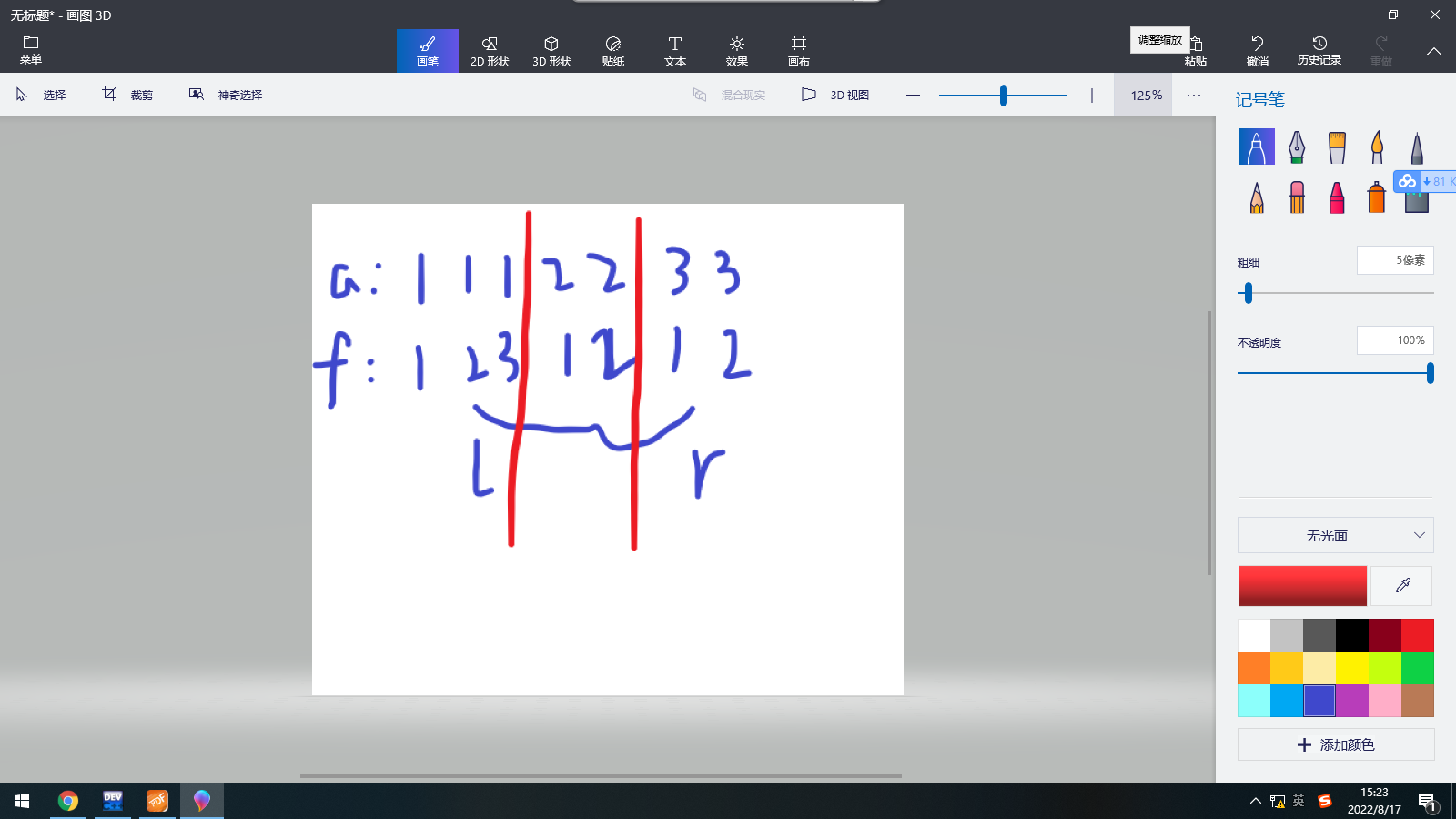
对于这种情况，查询到的应该是3，可是答案很显然是2。可以发现，对于每一个区间，可以分为三种情况

①：最左边的不完全元素。可以先排除这一部分

②：中间的完全元素部分，对于这一部分直接求最大值即可

③：最右边的不完全部分。这种情况其实不影响，可以融合在情况②中

综上，可以先求②③这一部分的最大值，然后单独看最左边元素的个数与②③这一部分的最大值谁更大一些

 

Code 
 #include <bits/stdc++.h>
using namespace std;
int num[100010], f[100010], MAX[100010][20];
int n;
void ST() {
  int i, j, k;
  for (i = 1; i <= n; i++) MAX[i][0] = f[i];
  k = log((double)(n + 1)) / log(2.0);
  for (j = 1; j <= k; j++)
    for (i = 1; i + (1 << j) - 1 <= n; i++)
      MAX[i][j] = max(MAX[i][j - 1], MAX[i + (1 << (j - 1))][j - 1]);
}
int rmq_max(int l, int r) {
  if (l > r)
    return 0;
  int k = log((double)(r - l + 1)) / log(2.0);
  return max(MAX[l][k], MAX[r - (1 << k) + 1][k]);
}
int main() {
  int q, i, a, b;
  while (scanf("%d", &n) && n) {
    scanf("%d", &q);
    for (i = 1; i <= n; i++) {
      scanf("%d", &num[i]);
      if (i == 1) {
        f[i] = 1;
        continue;
     }
      if (num[i] == num[i - 1])
        f[i] = f[i - 1] + 1;
      else
        f[i] = 1;
   }
    ST();
    for (i = 1; i <= q; i++) {
      scanf("%d%d", &a, &b);
      int t = a;
      while (t <= b && num[t] == num[t - 1]) t++;
      int cnt = rmq_max(t, b);
      int ans = max(t - a, cnt);
      printf("%d\n", ans);
   }
 }
  return 0;
}

 

金字塔

标签：区间DP

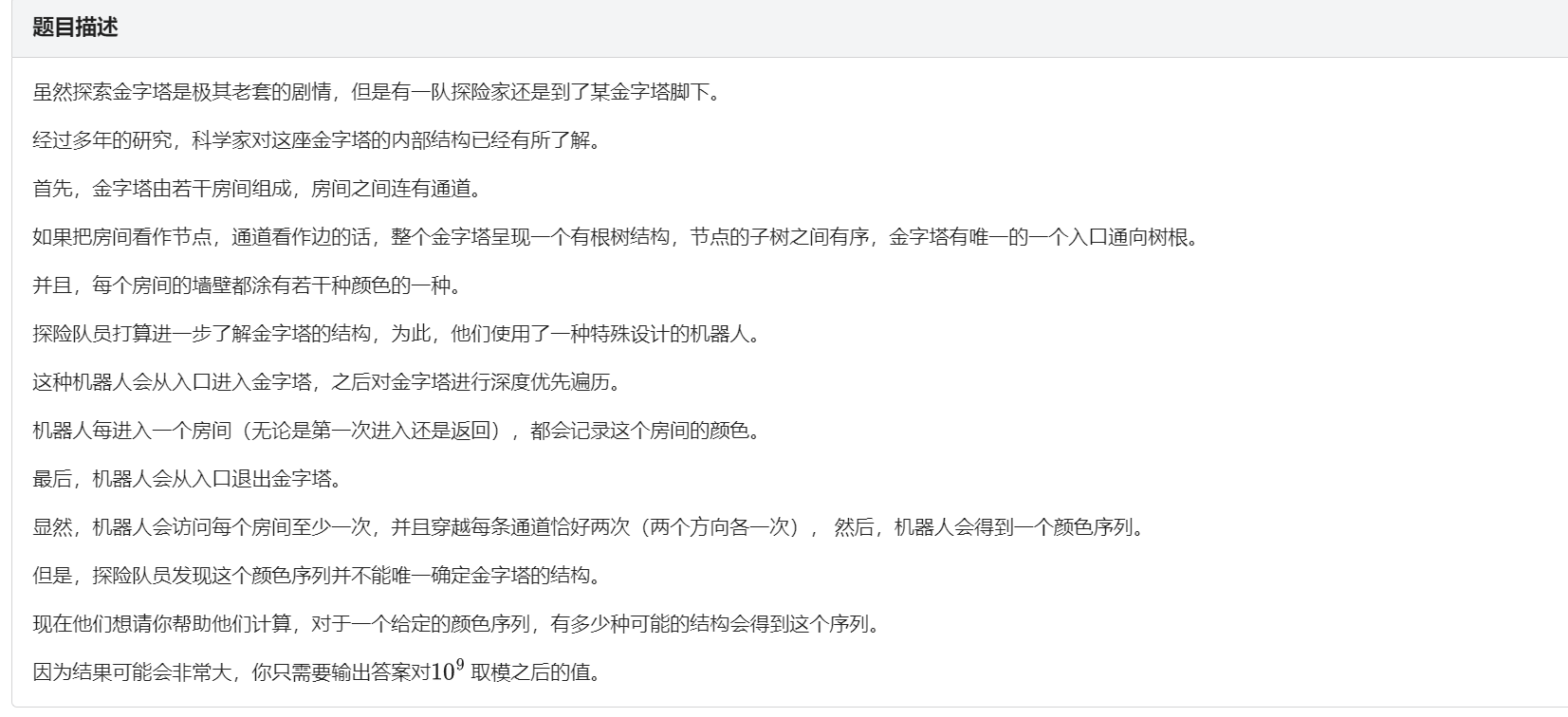
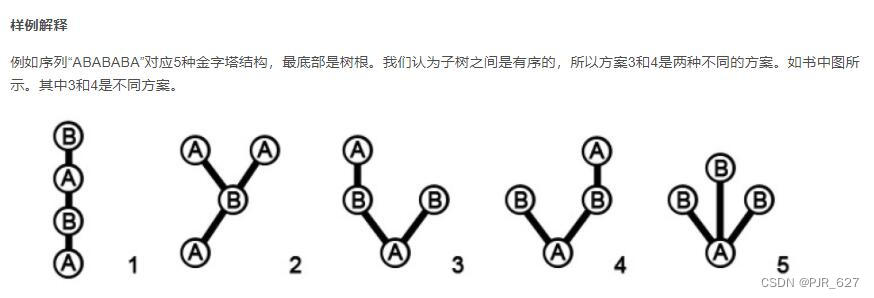
在题目中要求了最终要回到起点，所以其中一定会有重复的两种颜色，所以我们需要找到颜色相同的两个房间。

首先，我们先枚举区间，如图，我们首先找到了第一次重复出现的房间，也就是现在的根节点以及下个节点。（因为Graph Editor的某些原因，我就在节点后添上了序号）如图所示

                       

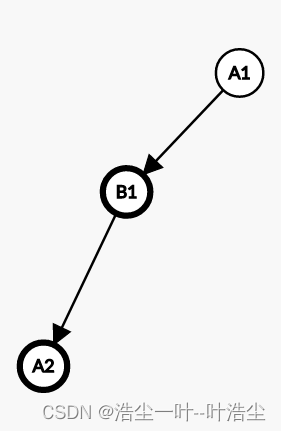
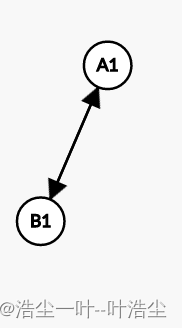
 有两种情况，①这两个点是一个；②两个点不是一个，所以，我们进行状态转移时也是要分两种情况分类讨论。

现在我们知道了思路，但是，方案数怎么计算呢?

我们要算相同节点之间的方案总数，只需要对中间节点进行枚举，把中间点的方案数相加即可。

还是一个问题到底怎么算？

学过加法原理和乘法原理的人都知道，将左部分的方案数乘上右部分的方案数便是总的方案数，所以便有状态转移方程：

f [ l ][ r ] = f [ l ][ r ] + f [ l + 1][ k - 1] * f [ k ][ r ];

 

Code 
#include<cstdio>
#include<cstring>
using namespace std;
const long long Mod = 1e9;
char s[305];
long long f[305][305];
int main(){
    scanf("%s",s+1);
    int n = strlen(s+1);
    for(int i = 1;i <= n;i++)
        f[i][i] = 1;
    for(int len = 3;len <= n;len++){
        for(int l = 1;l+len-1 <= n;l++){
            int r = l+len-1;
            if(s[l] != s[r]){ //首尾都不一样很显然不满足条件
                f[l][r] = 0;
                continue;
            }
            f[l][r] = f[l+1][r-1];
            for(int k = l+2;k <= r-2;k++)
                if(s[l] == s[k])
                    f[l][r] = (f[l][r]+f[l+1][k-1]*f[k][r]%Mod)%Mod;
        }
    }
    printf("%d",f[1][n]);
    return 0;

}

 

斗地主

标签：模拟

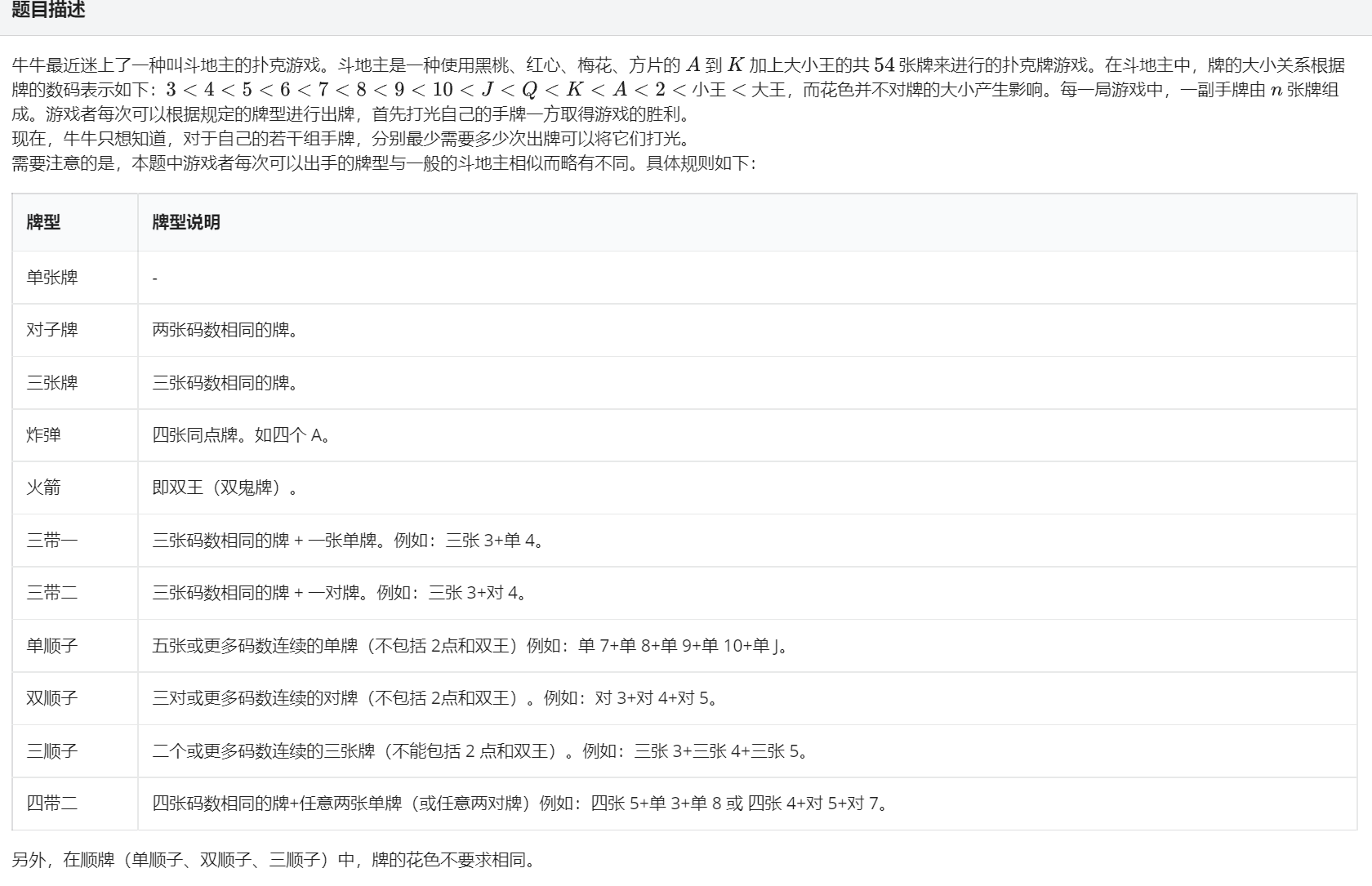
恶心的模拟

为了尽可能的简化我们对题目的描述，我们需要思考，在题目当中，有哪些内容是可以合并或者是可以优先选取的(需要注意， 我们的目标是尽可能快的出完手牌)。

1、因为双王在我们的手牌里不和其他任意牌形成组合，因此，我们可以把它当对子处理。
2、因为我们所有的出牌方式和这张牌的花色都没有关系，因此，不需要去管这个牌的花色是多少。
3、为了让我们的牌更符合常规（大小顺序为3<4<5<…<A<2 ）,因此我们将 记A为12 ，2 记为 13，大小王记为14 (当然，这个可以不单独记)，其他数全部减 2（包含 J,Q ,K ）,方便后续查找
4、除顺子外，其他的牌是出得越多越好（因为不会相互影响）且有时会存在不出顺子比出顺子更好的情

况。
5、在不出顺子的情况下，出牌的优先级为：四带两对->四带二->三带二->三带一->炸弹->三张牌->对子
牌->单张牌
6、将顺子全部排除出来，计算非顺子牌出牌的次数有多少（注意记录那些可以带的牌的数量），然后，用DFS去搜索，究竟是用这个顺子的答案更优还是不用这个顺子的答案更优。
7、注意炸弹也可以看成是两个对子组成的。因此，四带两对也可以使用四带四。

 

  首先，我们要把问题转化尽量容易处理，既具有一般性：那么我们可以把双王看作一副对牌，无视颜色，以及将k设为11,k设为12（其它依照题中所给顺序依次类推）等。
不难想到，我们要用最少的次数出完所有牌，那么对于非顺子的牌，当然是出的越多越好。
如有四张，就不要分成3张或两张来出，那样只会增加次数，对于三张和两张亦然。
同样的，如果可以带牌，当然要尽量选择减少次数多的来带，（注意不是排数最多的，因为我们最终的目标是用最少的次数出完牌）
例如四张的话，优先选择带两张单牌或两对对牌，这样均可减少两次次数，是在不行再选把一副对牌拆看，当单牌来带，这样只能减少一次。
非顺子牌利用贪心的思想解决了，那么顺子呢？
容易想到，顺子的选取是会对其它出牌方式产生影响的，因此我们可以采取爆搜（dfs+回溯）的方法搜顺子，在各种出顺子的方案中记录最小的即可。
为了提高效率，期间当然可采取最优性剪枝来优化。
  总结：通过该题不难看出，爆搜的题有一个特点，即需要利用dfs处理出结果，然后通过回溯进行多种解的比较，从中选出最优。

 

Code 
 #include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
int T, n, ans, s[15];
void dfs(int shunzi) {
  if (shunzi > ans)
    return;  //最优化剪枝
  int i, j, s1 = 0, s2 = 0, s3 = 0, s4 = 0, cnt = 0;
  //非顺子
  for (i = 1; i <= 14; i++)  //单牌需出的次数
    if (s[i] == 1)
      s1++;
  for (i = 1; i <= 14; i++)  //对牌需出的次数
    if (s[i] == 2)
      s2++;
  for (i = 1; i <= 14; i++)  //三带
 {
    if (s[i] == 3) {
      s3++;
      if (s1 >= 1)
        s1--;  //三带优先带单
      else if (s2 >= 1)
        s2--;  //其次带双
   }
 }
  for (i = 1; i <= 14; i++)  //四带
 {
    if (s[i] == 4) {
      if (cnt)
        cnt--;
      else {
        s4++;
        if (s1 >= 2)
          s1 -= 2;  //四代优先带两个单
        else {
          if (s2 >= 2)
            s2 -= 2;  //其次是带双
          else if (s2 >= 1)
            s2--;  //最后带单
          else
            cnt++;
       }
     }
   }
 }
  //取当前最优解
  ans = min(ans, shunzi + s1 + s2 + s3 + s4);
  for (i = 1; i <= 8; i++)  //单顺起点
 {
    for (j = i; j <= 12; j++)  //单顺终点
   {
      s[j]--;
      if (s[j] < 0)
        break;
      if (j - i >= 4)
        dfs(shunzi + 1);
   }
    if (j == 13)
      j--;
    while (j >= i)  //回溯
   {
      s[j]++;
      j--;
   }
 }
  for (i = 1; i <= 10; i++)  //双顺起点
 {
    for (j = i; j <= 12; j++)  //双顺终点
   {
      s[j] -= 2;
      if (s[j] < 0)
        break;
      if (j - i >= 2)
        dfs(shunzi + 1);
   }
    if (j == 13)
      j--;
    while (j >= i)  //回溯
   {
      s[j] += 2;
      j--;
   }
 }
  for (i = 1; i <= 11; i++)  //三顺
 {
    for (j = i; j <= 12; j++) {
      s[j] -= 3;
      if (s[j] < 0)
        break;
      if (j - i >= 1)
        dfs(shunzi + 1);
   }
    if (j == 13)
      j--;
    while (j >= i) {
      s[j] += 3;
      j--;
   }
 }
  return;
}
int main() {
  scanf("%d%d", &T, &n);
  while (T--) {
    memset(s, 0, sizeof(s));
    int i, a, b;
    ans = 54;
    for (i = 1; i <= n; i++) {
      scanf("%d%d", &a, &b);
      if (a == 0)
        s[14]++;  // s统计数量，14表示王牌
      if (a == 1)
        s[12]++;  // A相当于12
      if (a == 2)
}

 

网络连接

标签：模拟

 

 

Code 
 #include<bits/stdc++.h>
using namespace std;
int n;
int tot;
string q[10005];
int ans[10005];
bool check(string s,int len)
{
	bool flg=0;
	int bj1=0,bj2=0;
	int cnt=0;
	long long p[105],q[105];
	memset(p,0,sizeof(p));
	for(int i=0;i<=100;++i)
	q[0]=-1;
	for(int i=0;i<len;++i)
	{
		if(bj2==1&&bj1<3)
		return 0;
		if(cnt+1<=bj1+bj2) 
		return 0;
		if(s[i]=='0') 
		{
			if(flg==0)
			cnt++;
			q[cnt]=0;
			if(i>=0) 
			{
				if(flg==0&&((s[i-1]<='9'&&s[i-1]>='0')||(s[i+1]<='9'&&s[i+1]>='0')))
				{
					return 0;
				}
			}
			else
			{
				if(flg==0&&(s[i+1]<='9'&&s[i+1]>='0'))
				{
					return 0;
				}	
			}
			flg=1;
			p[cnt]*=10;
		}
		else if(s[i]=='-') 
		return 0;
		else if(s[i]=='.') 
		{
			bj1++;
			flg=0;
		}
		else if(s[i]==':')
		{
			bj2++;
			flg=0;
		}
		else if(s[i]>='1'&&s[i]<='9') 
		{
			if(flg==0)
			cnt++;
			q[cnt]=0;
			p[cnt]=p[cnt]*10+s[i]-'0'; 
			flg=1;
		}
		else 
		return 0;
	}
	if(p[1]<=255&&p[2]<=255&&p[3]<=255&&p[4]<=255&&p[5]<=65535&&cnt==5&&bj1==3&&bj2==1&&q[1]>=0&&q[2]>=0&&q[3]>=0&&q[4]>=0&&q[5]>=0)//奇奇怪怪的判断 
	return 1;
	else
	return 0;
}
int main()
{
// 	freopen("network.in","r",stdin);
// 	freopen("network.out","w",stdout);
	scanf("%d",&n);
	for(int i=1;i<=n;++i) 
	{
		string op,s;
		cin>>op>>s;
		if(!check(s,s.length()))
		{
			printf("ERR\n");
			continue;
		}
		bool flg=0;
		if(op=="Server")
		{ 
			for(int j=1;j<=tot;++j)
			{
				if(s==q[j])
				{
					flg=1;
					break;
				}
			}
			if(flg==0)
			{
				printf("OK\n");
				q[++tot]=s;
				ans[tot]=i;
			}
			else
			{
				printf("FAIL\n");
			}
		}
		else
		{ 
			for(int j=1;j<=tot;++j)
			{
				if(q[j]==s)
				{
					printf("%d\n",ans[j]);
					flg=1;
					break;
				}
			}
			if(flg==0)
			{
				printf("FAIL\n");
			}
		}
	}
	return 0; 
}
posted @ 2022-08-17 21:04  Doria_tt  阅读(51)  评论(0)    收藏  举报